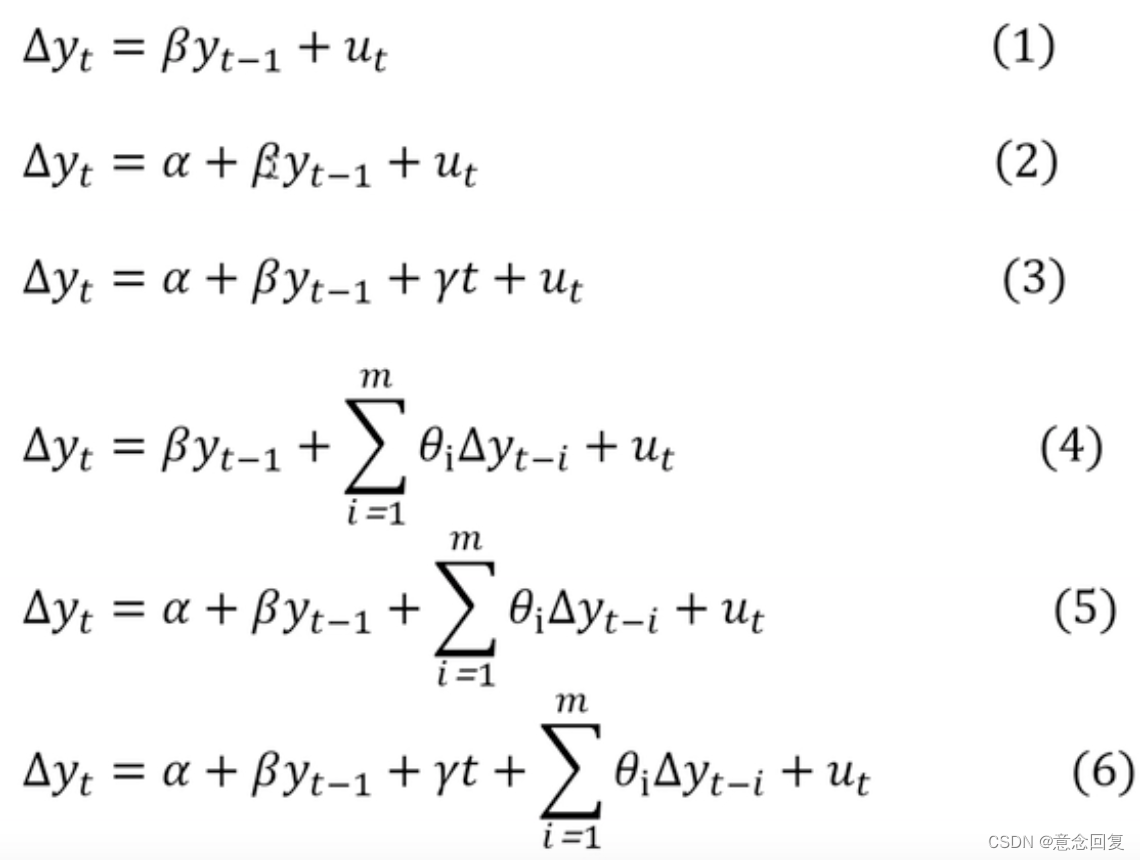在资本资产定价模型（CAPM）中，β系数也称为贝塔系数（Beta coefficient），是一种风险指数，用来衡量个别股票或股票基金相对于整个股市的价格波动情况。如果β系数不具有稳定性，CAPM将不再适用，所以，检验β系数的稳定是很有必要的。

数据的获取

个股的β数据可从锐思数据库（RESSET）中获取，详情参见上一篇博客
基于SPSS的正态性检验方法汇总——以个股收益率为例（超详细）

注意风险因子β选择流通市值加权。

将Excel数据导入到Eviews

打开Eviews软件，选择Open a Foreign file (such as Excel)
如果打开报错，说明需要在Excel中进行设置。

Excel中选择文件—选项

选项中点击加载项，在管理处选择COM加载项并点击转到。
将可用加载项全部不勾选，然后点击确定并保存，即可成功导入到Eviews中。

一直点击下一步，嫌麻烦可以直接点完成。

询问处点Yes。

Eviews无法识别中文，所有中文处均用下划线代替。

时间序列图

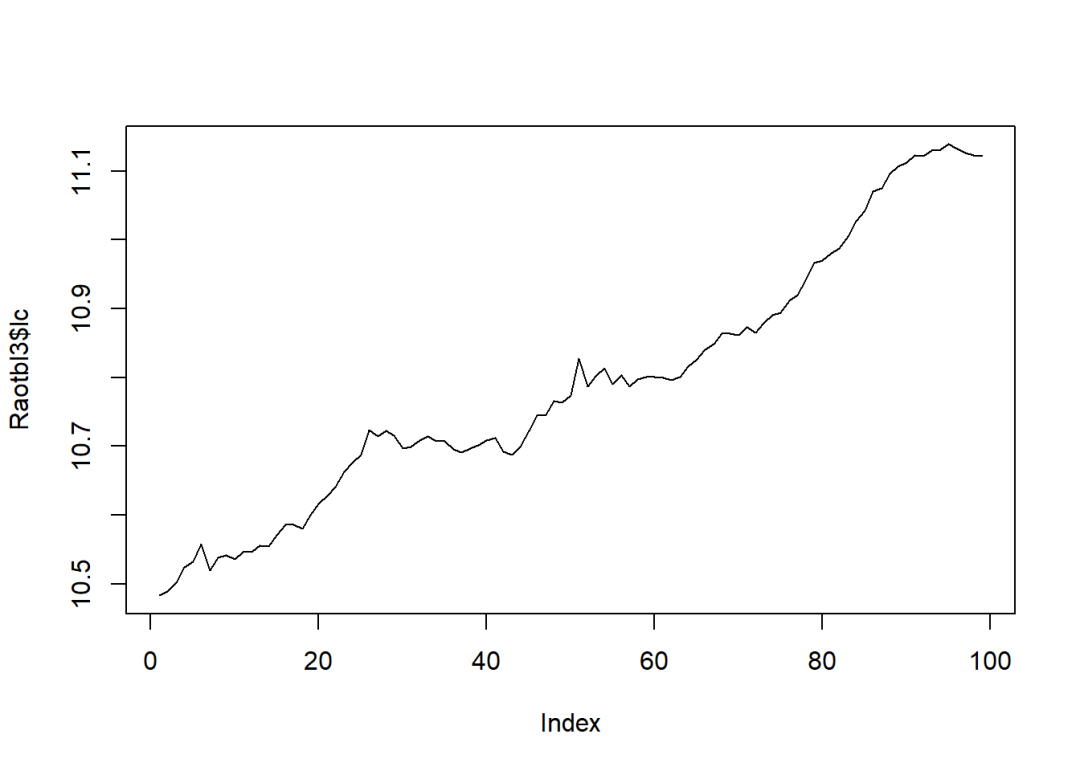
双击第一个“____________…”，然后点View—Graph即可绘制数据的时间序列图。

选择图的类型。

即可得到β系数的时间序列图。

单位根检验与ADF检验

单位根检验是指检验序列中是否存在单位根，因为存在单位根就是非平稳时间序列了。单位根就是指单位根过程，可以证明，序列中存在单位根过程就不平稳，会使回归分析中存在伪回归。
DF检验与ADF检验均是基于单位根检验。Dickey-Fuller通过研究发现t统计量在原假设下已经不再服从t分布。为此,Mackinnon进行了大规模的模拟，给出了在单变量情况下不同回归模型以及不同样本数下t统计量在1%、5%和10%显著性水平下的临界值。这样，就可以根据需要，选择适当的显著性水平，通过t统计量来决定是否接受或拒绝原假设。这一检验被称为Dickey-Fuller检验（DF检验）。
上面描述的单位根检验只有当序列为AR（1）时才有效。如果序列存在高阶滞后相关，这就违背了扰动项是独立同分布的假设。在这种情况下，Dickey-Fuller提出了使用增厂的DF检验方法(Augmented Dickey-Fuller test )来检验含有高阶序列相关的序列的单位根。

个股的β系数稳定性检验

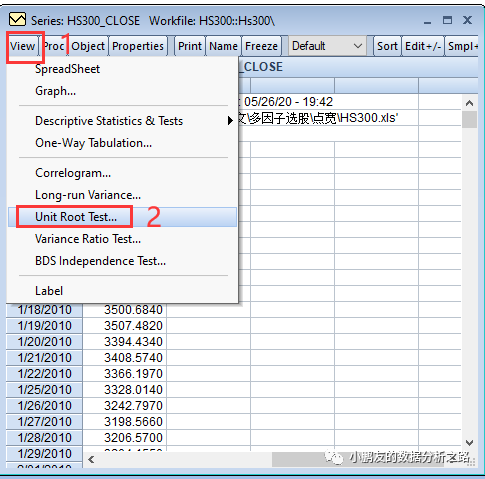
View—Unit Root Test…
Test type 选择 Augmented Dickey-Fuller
Test for unit root in 中 Level 表示原时间序列，1st difference表示一阶差分，2nd difference 表示二阶差分，只检验原序列的稳定性只选Level就可以。
Include in test equation 中Intercept 表示截距项，Trend and intercept 表示趋势项和截距项，None 表示两者均无，如果可以从时间序列图中很明显的看出是否有趋势项或截距项选择一个就可以，如果不能直接观察出来需要依次选三个然后进行比较。
右边的内容不需要改。

首先选择截距项，计算结果如下图所示。
先看圈1，ADF检验的 t-Statistic 大于下面1%、5%、10%level的任意一个 t-Statistic，说明只存在截距项时，不拒绝原假设，存在单位根，序列非平稳。
再看圈2中AIF、SC、HQ的值，先将其记录下来，与后两种情况三者的值进行比较。
点击Freeze，将窗口冻结后继续点View—Unit Root Test…
Test type 选择 Augmented Dickey-Fuller，Test for unit root in 选择Level ，Include in test equation 选择 Trend and intercep。
结果与上一种情况相同，不拒绝原假设，存在单位根，序列非平稳。再记录下AIF、SC、HQ的值。

点击Freeze，将窗口冻结后继续点View—Unit Root Test…
Test type 选择 Augmented Dickey-Fuller，Test for unit root in 选择Level ，Include in test equation 选择 None。
结果与上一种情况相同，不拒绝原假设，存在单位根，序列非平稳。再记录下AIF、SC、HQ的值。

三种情形下，比较检验模型对应的AIC、SC、HQ的值，找出最小的情况。

在截距项和趋势项都无的情况下，AIC、SC、HQ的值均最小，故根据这一情况下的检验，该股票的β系数的时间序列为截距项和趋势项都无的单位根过程，即非平稳过程。

补充

对于ADF检验结果，
若m>C>B>A，则不拒绝原假设；
若C>m>B>A，则在5%的显著性水平下不拒绝原假设；
若C>B>m>A，则在1%的显著性水平下不拒绝原假设；
若C>B>A>m，则拒绝原假设。
一般情况下根据5%level的值来判断，即若m>B，则不拒绝原假设，存在单位根，序列非平稳；若m<B，则拒绝原假设，不存在单位根，序列平稳。也可根据实际情况选择更严格或更宽松的假设条件。

总结

使用CAPM之前，应对股票β系数的稳定性进行检验。个别股票的β系数并不稳定，此时不能简单地套用CAPM。