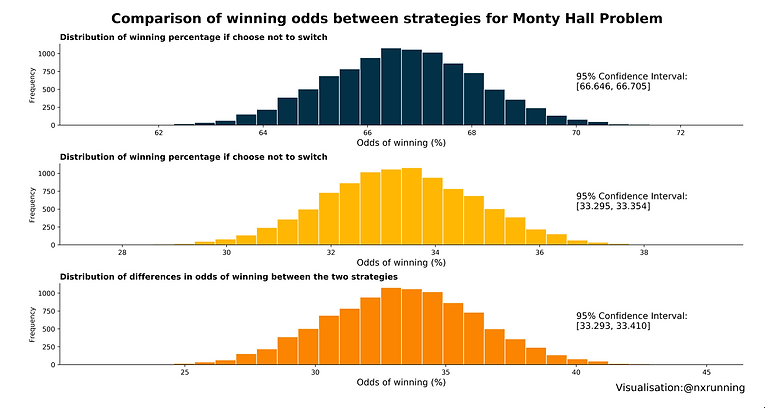
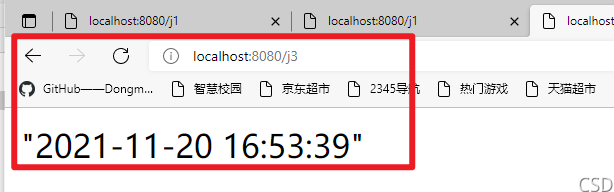
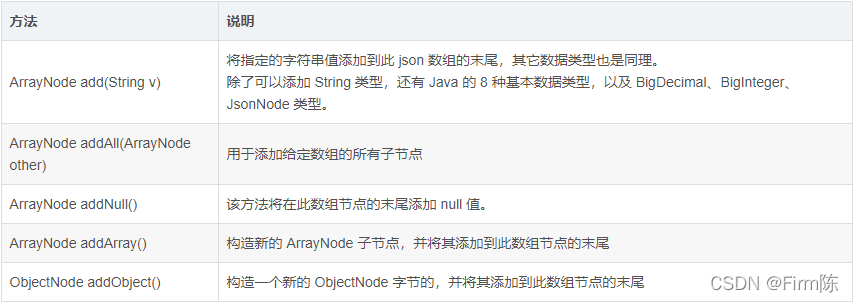
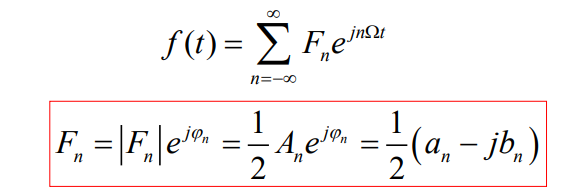1 A simple definition:
Little’s Law states that the long-term average number of customers in a stable system L L L is equal to the long-term average effective arrival rate, λ \lambda λ, multiplied by the average time a customer spends in the system, W W W.
Expressed algebraically, Little’s law appears quite simple: L = λ W L = \lambda W L=λW
L L L represents a business’ average number of customers.
λ \lambda λ refers to these customers’ arrival rate (assuming an identical departure rate).
W W W symbolizes the average amount of time customers spend at the business.
When calculating L, the number of people at a business, simply invert the equation: λ W = L \lambda W = L λW=L

2 Mathematical definition:
In mathematical queueing theory, Little’s result, theorem, lemma, law, or formula is a theorem by John Little which states that the long-term average number L of customers in a stationary system is equal to the long-term average effective arrival rate λ \lambda λ multiplied by the average time W W W that a customer spends in the system. Expressed algebraically the law is The relationship is not influenced by the arrival process distribution, the service distribution, the service order, or practically anything else. In most queuing systems, service time is the bottleneck that creates the queue.
L = λ W L = \lambda W L=λW
The result applies to any system, and particularly, it applies to systems within systems. For example in a bank branch, the customer line might be one subsystem, and each of the tellers another subsystem, and Little’s result could be applied to each one, as well as the whole thing. The only requirements are that the system be stable and non-preemptive; this rules out transition states such as initial startup or shutdown.
In some cases it is possible not only to mathematically relate the average number in the system to the average wait but even to relate the entire probability distribution (and moments) of the number in the system to the wait.
3 Example
Imagine 20 customers visit your hip and trendy taco truck every hour (λ = 10). They stick around for half an hour (W = .5), eating and chatting with each other. At any given time, you would have an average of 10 customers standing around your foodtruck and enjoying your organic, grass-fed shitake mushroom and carne asada burritos:
λ W = L
20 x .5 = 10
Now, imagine you hired a team of acrobatic sign-spinners to promote your business and this effort doubled your arrival rate to 40/hour. You would have to chase people away from your truck with squirt guns to make room for new customers:
40 x .25 = 10
…or cut a second serving window in the side of your truck to serve two lines of customers:
40 x .5 = 20
Now that you’ve wrapped your head around the basics of Little’s Law (and worked up an appetite), you can appreciate how corporate leaders use this little formula to manage workflow and increase efficiency
4 利特尔法则
利特尔法则(英语:Little’s law),基于等候理论,由约翰·利特尔在1954年提出。利特尔法则
可用于一个稳定的、非占先式的系统中。其内容为:
在一个稳定的系统中,长期的平均顾客人数(L),等于长期的有效抵达率(λ),乘以顾客在这个系统中平均的等待时间(W);
或者,我们可以用一个代数式来表达:
L = λ W L = \lambda W L=λW
利特尔法则可用来确定在途存货的数量。此法则认为,系统中的平均存货等于存货单位离开系统的比率(亦即平均需求率)与存货单位在系统中平均时间的乘积。
虽然此公式看起来直觉性的合理,它依然是个非常杰出的推导结果,因为此一关系式“不受到货流 程分配、服务分配、服务顺序,或任何其他因素影响”。
此一理论适用于所有系统,而且它甚至更适合用于系统中的系统。举例来说,在一间银行里,顾客等待的队伍就是一个子系统,而每一位柜员也可以被视为一个等待的子系统,而利特尔法则可以套用到任何一个子系统,也可以套用到整个银行的等待队伍之母系统。
唯一的条件就是,这个系统必须是长期稳定的,而且不能有插队抢先的情况发生,这样才能排除换场状况的可能性,例如开业或是关厂