文章目录
- 周期信号的傅里叶级数
- 1 周期信号三角形式的傅里叶级数
- 1.1 三角形式的傅里叶级数
- 1.2 狄里赫利(Dirichlet)条件
- 1.3 .余弦形式的傅里叶级数
- 1.4 吉布斯现象
- 2 周期信号波形对称性和谐波特性
- 3 指数形式的傅里叶级数
- 4 两种傅里叶级数展开形式的关系
周期信号的傅里叶级数
1 周期信号三角形式的傅里叶级数
1.1 三角形式的傅里叶级数
广义傅里叶级数的 φ i ( t ) \varphi_i(t) φi(t)选三角函数。

设周期信号 f ( t ) f(t) f(t),其周期为 T T T,角频率(基波频率) Ω = 2 π / T \Omega=2\pi/T Ω=2π/T,当满足狄里赫利(Dirichlet)条件时,可展开为三角形式的傅里叶级数。

系数 a n , b n a_n, b_n an,bn称为傅里叶系数。
由

得到 a n , b n a_n,b_n an,bn:

其中 a 0 2 \frac{a_0}{2} 2a0对应1的系数, K i = T / 2 K_i=T/2 Ki=T/2。
知道原函数 f ( t ) f(t) f(t)就知道周期 T T T,然后可以求得 Ω \Omega Ω
注意:积分区间不一定要 [ − T 2 , T 2 ] [-\frac{T}{2},\frac{T}{2}] [−2T,2T],只要是个整周期区间就行,比如 [ 0 , T ] [0,T] [0,T]
写成 a 0 2 \frac{a_0}{2} 2a0的原因:使得 a 0 = 2 T ∫ − T 2 T 2 f ( t ) d t a_{0}=\frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) \mathrm{d} t a0=T2∫−2T2Tf(t)dt可以包含在 a n a_n an里面。
n = 0 n=0 n=0时, b 0 = 0 , 因 为 s i n ( 0 Ω t ) = 0 b_0=0,因为sin(0\Omega t)=0 b0=0,因为sin(0Ωt)=0
a n a_n an为 n n n的偶函数, b n b_n bn为 n n n的奇函数
1.2 狄里赫利(Dirichlet)条件
条件1:在一个周期内,函数连续或只有有限个第一类间断点(间断点左右极限都存在);
反例(无限个第一类间断点):
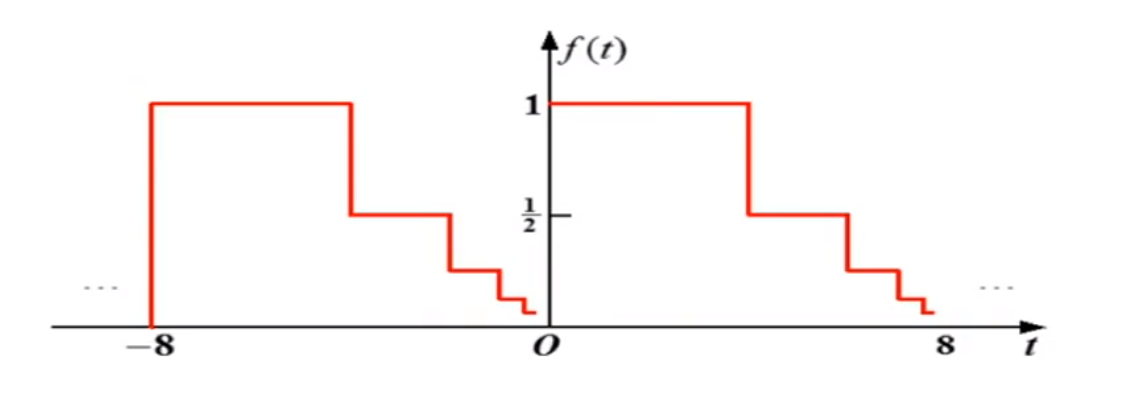
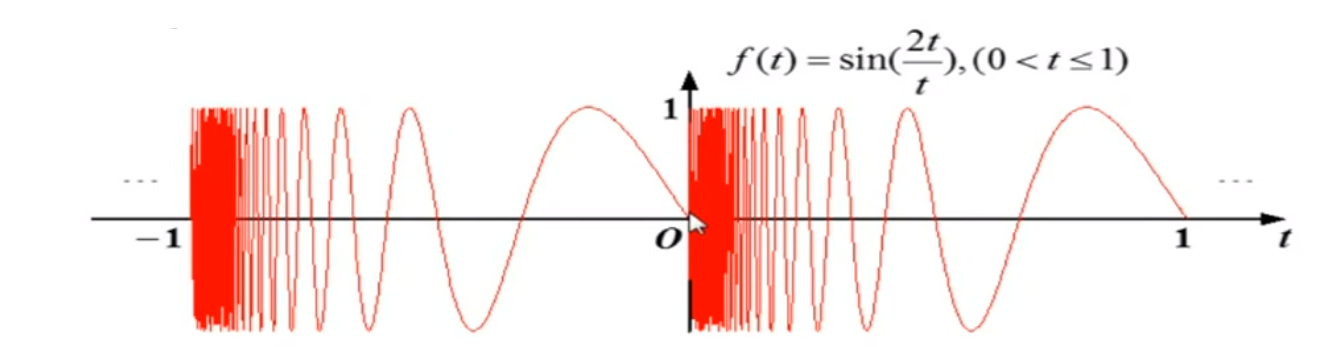
条件2:在一个周期内,函数极大值和极小值的数目应为有限个;
反例:
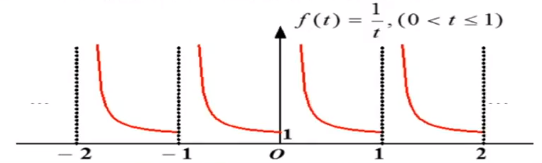
条件3:在一个周期内,函数绝对可积。
反例:
1.3 .余弦形式的傅里叶级数
由辅助角公式:
a sin x + b cos x = a 2 + b 2 sin ( x + ϕ ) , 其中 tan ϕ = b / a a\sin x+b\cos x=\sqrt{a^2+b^2} \sin ({x}+\phi), \quad \text { 其中 } \tan \phi=b / a asinx+bcosx=a2+b2sin(x+ϕ), 其中 tanϕ=b/a
或:
a sin x + b cos x = a 2 + b 2 cos ( x + ϕ ) , 其中 tan ϕ = − a / b a\sin x+b\cos x=\sqrt{a^2+b^2} \cos ({x}+\phi), \quad \text { 其中 } \tan \phi=-a / b asinx+bcosx=a2+b2cos(x+ϕ), 其中 tanϕ=−a/b

含义:周期信号可分解为直流和许多余弦分量。



1.4 吉布斯现象
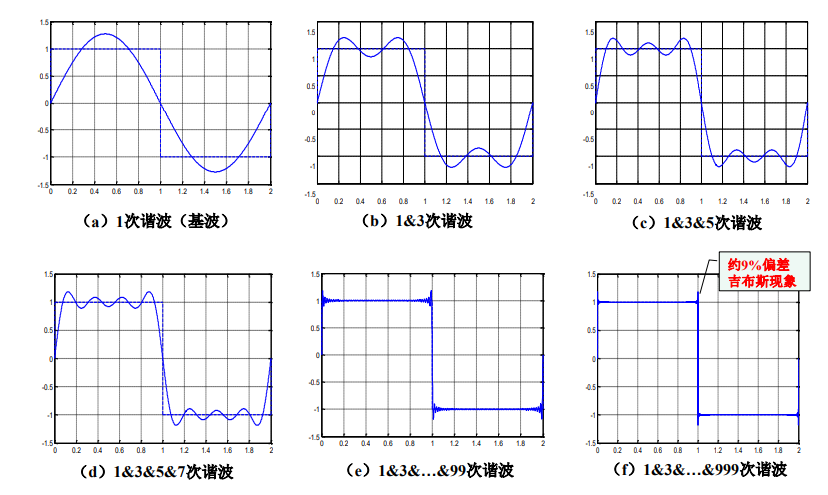
用有限项傅里叶级数表示有间断点的信号时,在间断点附近不可避免的会出现振荡和超调量。超调量的幅度不会随所取项数的增加而减小。只是随着项数的增多,振荡频率变高,并向间断点处压缩,从而使它所占有的能量减少。
当选取的项数很大时,该超调量趋于一个常数,大约等于总跳变值的9%,并从间断点开始以起伏振荡的形式逐渐衰减下去。这种现象称为吉布斯现象。
2 周期信号波形对称性和谐波特性
2.1 f ( t ) f(t) f(t)为偶函数
——对称于纵轴 f ( t ) = f ( − t ) f(t) =f(-t) f(t)=f(−t)

f ( t ) f(t) f(t)为偶函数, sin ( n Ω t ) \sin(n\Omega t) sin(nΩt)为奇函数,偶函数乘奇函数是奇函数,在 [ − T 2 , T 2 ] [-\frac{T}{2},\frac{T}{2}] [−2T,2T]积分为零。
2.2 f ( t ) f(t) f(t)为奇函数
——对称于原点 f ( t ) = − f ( − t ) f(t) =-f(-t) f(t)=−f(−t)
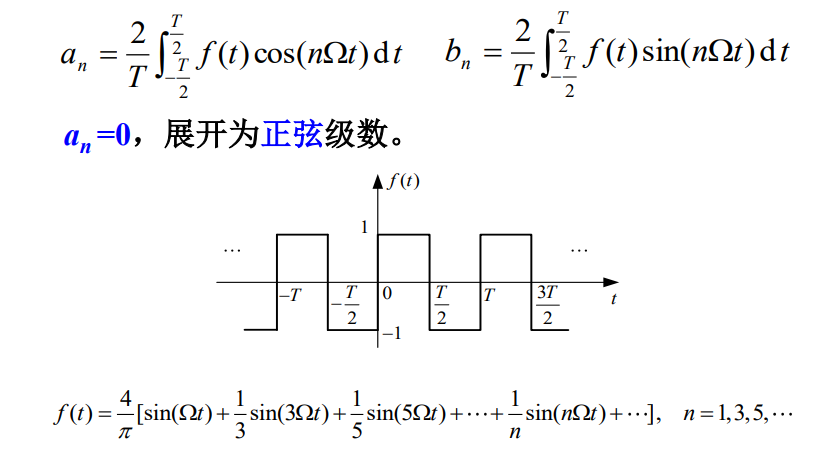
f ( t ) f(t) f(t)为奇函数, c o s ( n Ω t ) cos(n\Omega t) cos(nΩt)为偶函数,奇函数乘偶函数是奇函数,在 [ − T 2 , T 2 ] [-\frac{T}{2},\frac{T}{2}] [−2T,2T]积分为零。
2.3 f ( t ) f(t) f(t)为奇谐函数
—— f ( t ) = – f ( t ± T / 2 ) f(t) = –f(t±T/2) f(t)=–f(t±T/2)
其傅里叶级数中只含奇次谐波分量,而不含偶次谐波分量,即:
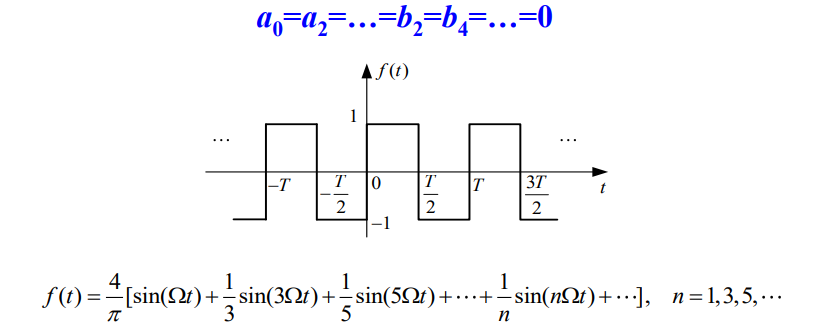
因为奇谐函数也是奇函数,所以也不含 cos \cos cos项。
2.4 f ( t ) f(t) f(t)为偶谐函数
—— f ( t ) = f ( t ± T / 2 ) f(t) = f(t±T/2) f(t)=f(t±T/2)
其傅里叶级数中只含偶次谐波分量,而不含奇次谐波分量,即
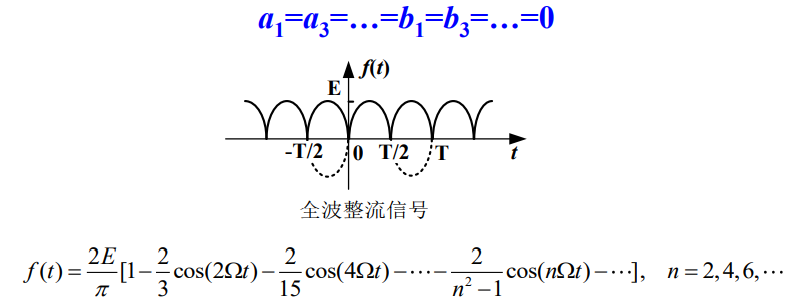
因为偶谐函数也是偶函数,所以也不含 sin \sin sin项。
cos ( 0 ) = 1 \cos(0)=1 cos(0)=1
偶协函数可以看成周期为 T / 2 T/2 T/2,则基波频率为 Ω ′ = 2 π / ( T / 2 ) = 4 Ω \Omega'=2\pi/(T/2)=4\Omega Ω′=2π/(T/2)=4Ω。
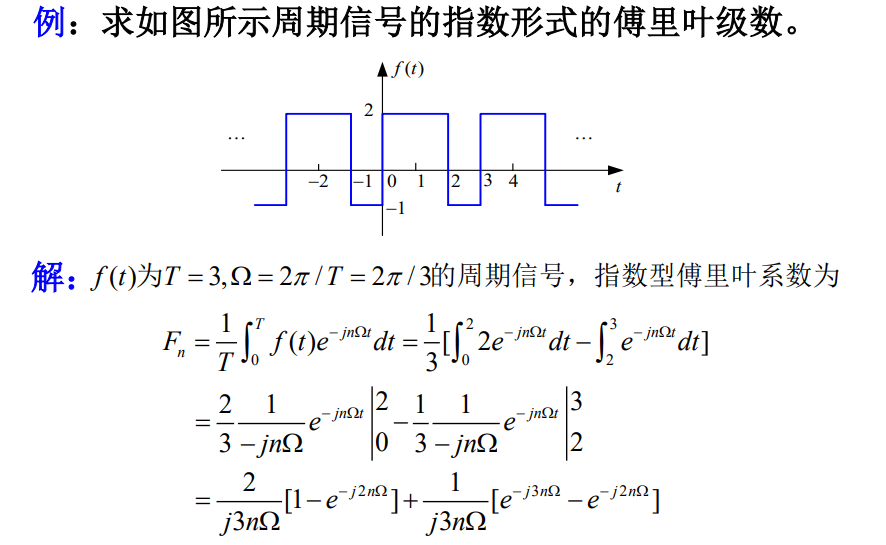
3 指数形式的傅里叶级数
欧拉公式:
e j x = cos x + sin x e^{jx}=\cos x+\sin x ejx=cosx+sinx
sin x = e i x − e − i x 2 \sin x=\frac{e^{ix}-e^{-ix}}{2} sinx=2eix−e−ix
cos x = e i x + e − i x 2 \cos x=\frac{e^{ix}+e^{-ix}}{2} cosx=2eix+e−ix
三角形式的傅里叶级数,含义比较明确,但运算常感不便,因而经常采用指数形式的傅里叶级数。

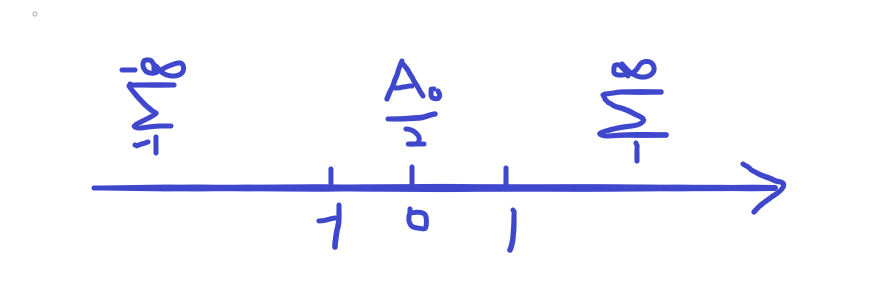
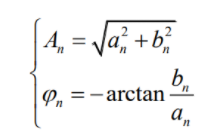
A n A_n An为偶函数, φ n \varphi_n φn为奇函数。
a n a_n an为关于 n n n的偶函数, b n b_n bn为关于 n n n的奇函数。 b n a n \frac{b_n}{a_n} anbn为关于 n n n的奇函数, arctan \text{arctan} arctan为奇函数, φ n = 奇 函 数 ( 奇 函 数 ) \varphi_n=奇函数(奇函数) φn=奇函数(奇函数)也为关于 n n n的奇函数。
得到:
f ( t ) = 1 2 ∑ n = − ∞ ∞ A n e j φ n e j n Ω t f(t)=\frac{1}{2} \sum_{n=-\infty}^{\infty} A_{n} \mathrm{e}^{j \varphi_{n}} \mathrm{e}^{j n \Omega t} f(t)=21n=−∞∑∞AnejφnejnΩt
e j n Ω t \mathrm{e}^{j n \Omega t} ejnΩt为指数信号。


表明:任意周期信号f(t)可分解为许多不同频率的虚指数信号之和。 F n F_n Fn是频率为 n Ω nΩ nΩ的分量的系数, F 0 = A 0 / 2 F_0 = A_0/2 F0=A0/2为直流分量。

e − j 2 π n = cos ( − 2 π n ) + j sin ( − 2 π n ) = 1 e^{-j2\pi n}=\cos(-2\pi n)+j\sin(-2\pi n)=1 e−j2πn=cos(−2πn)+jsin(−2πn)=1
4 两种傅里叶级数展开形式的关系
三角形式的傅里叶级数:

指数形式的傅里叶级数:
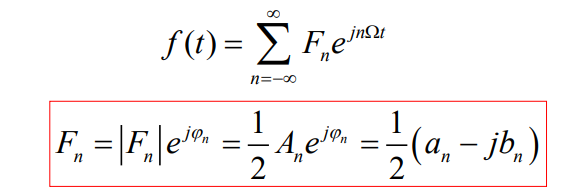
A n = 2 ∣ F n ∣ A_n=2|F_n| An=2∣Fn∣
我们要根据需要选择展开的形式。
《工程信号与系统》作者:郭宝龙等
中国大学MOOC:信号与系统 ,西安电子科技大学,郭宝龙,朱娟娟













![[ARM+Linux] 基于wiringPi库的串口通信](https://img-blog.csdnimg.cn/9ee83239c1034c5f90b6f223c348f377.png)