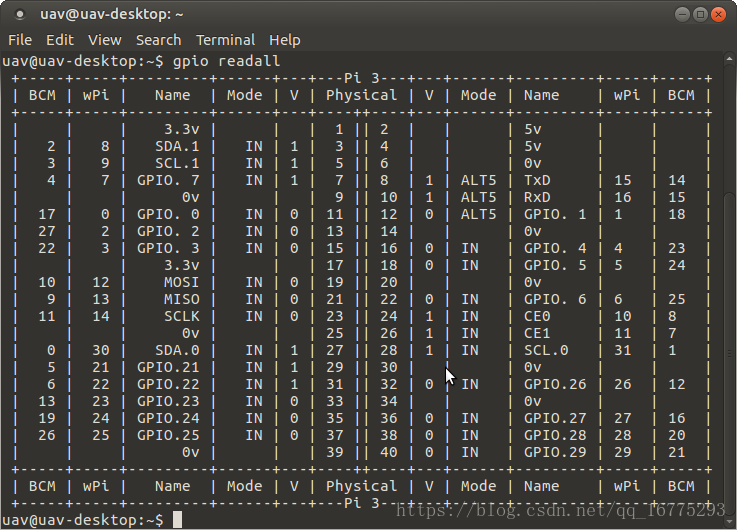
理解拉普拉斯变换，可以先从傅里叶变换开始。

傅里叶定律：只要一个函数满足如狄利赫里条件，都能分解为复指数函数之和。

狄利赫里条件：

(1) 函数在任意有限区间内连续，或只有有限个第一类间断点；

(2)在一个周期内，函数有有限个极大值或极小值；

(3) x(t) 在绝对可积，即 

当满足狄利赫里条件时，傅里叶变换及其逆变换为：

但是傅里叶变换有一个很大局限性，那就是信号必须满足狄利赫里条件才行，特别是绝对可积的条件。

于是我们可以把不满足绝对的可积的函数乘以一个快速衰减的函数，这样在趋于 ∞ 时原函数也衰减到零了，从而满足绝对可积。

数学描述是：

为保证  一直为衰减函数，我们把 x定义域缩减到正半轴，这样可以进行傅里叶变换就变成了：

如果假设： ， 那么就得到：

这就是拉普拉斯变换。