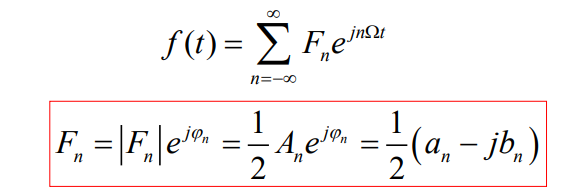一、周期信号的频域描述

1. 狄里赫利条件

（1）函数在任意有限区间内连续，或只有有限个第一类间断点

（2）在一个周期内，函数有有限个 极大值或极小值

2. 傅里叶级数

（1）傅里叶级数的三角函数表达

在有限区间上，一个周期信号x(t)满足狄里赫利条件时可以展开

设信号的周期为T

(omega_0 = frac{2pi}{T})

(x(t) = frac{a_0}{2} + sum_{n = 1}^{infty}(a_ncosnomega_0t + b_nsinnomega_0t))

(a_n = frac{2}{T}int_{-T/2}^{T/2}x(t)cosnomega_0tdt, n = 1, 2, cdots)

(b_n = frac{2}{T}int_{-T/2}^{T/2}x(t)sinnomega_0tdt, n = 1, 2, cdots)

经变换后可以得到另一种形式的表达

(x(t) = frac{a_0}{2} + sum_{n = 1}^{infty}A_ncos(nomega_0t + phi_n))

(A_n = sqrt{a_n^2 + b_n^2})

(phi_n = -arctg(frac{b_n}{a_n}))

比较两种表达方式可知

(a_n = A_ncosphi_n)

(b_n = -A_nsinphi_n)

由于n是整数，故周期信号的频谱是离散的

（2）傅里叶级数的指数表达

由欧拉公式可知

(cosomega t = frac{1}{2}(e^{-jomega t} + e^{jomega t}))

(sinomega t = frac{1}{2}(e^{-jomega t} - e^{jomega t}))

指数表达为

(x(t) = C_0 + sum_{n = 1}^{infty}C_{-n}e^{-jnomega t} + sum_{n = 1}^{infty}C_ne^{jnomega_0t} n = 1, 2, 3, cdots)

(C_n = frac{1}{2}(a_n - jb_n))

(C_-n = frac{1}{2}(a_n + jb_n))

(C_0 = frac{a_0}{2})

简化表达式为

(x(t) = sum_{n = -infty}^{infty}C_ne^{jnomega_0t} n = 0, pm 1, pm 2, cdots)

(C_n = frac{1}{T}[int_{-T/2}^{T/2}x(t)cosnomega_0tdt - jint_{-T/2}^{T/2}x(t)sinnomega_0tdt])

(C_n = frac{1}{T}int_{-T/2}^{T/2}x(t)e^{-jnomega_0t}dt (n = 0, pm 1, pm 2, cdots))

3. 离散频谱的两个重要性质

（1）每个实周期函数的幅值谱是n((nomega_0))的偶函数

（2）当周期信号有时间移位(tau)时，其振幅谱不变，相位谱发生(pm nomega_0 tau)弧度的变化

4. 傅里叶级数的两种展开形式

（1）由三角函数表达的傅里叶级数的频谱是单边谱，角频率的变化范围是(0 ~ +infty)

（2）由复指数表达的傅里叶级数的频谱是双边谱，角频率的变化范围是(-infty~infty)

  

从图中也可以看出双边幅值谱是一个偶函数

5. 周期信号的频谱特点

（1）周期信号的频谱是离散谱

（2）周期信号的谱线仅出现在基波及各次谐波频率处

（3）周期信号的幅值谱中各频率分量的幅值随着频率的升高而减小，频率越高，幅值越小。

二、周期矩形脉冲的频谱

1. 基本原理

根据傅里叶级数理论知道，周期矩形脉冲信号的傅里叶级数为：

(f(t) = frac{Atau}{T}sum_{n=-infty}^{infty}Sa(frac{n2pi}{T}frac{tau}{2})e^{jnomega_0t} = frac{Atau}{T}sum_{n=-infty}^{n=infty}sinc(frac{ntau}{T})e^{jnomega_0t})

该信号第n次谐波的振幅为：

(F_n = frac{Atau}{T}Sa(frac{npi tau}{T}) = frac{Atau}{T}sinc(frac{ntau}{T}))

各谱线之间间隔为(frac{2pi}{T})。

 

 

2. 周期矩形脉冲的频谱特点

（1）与一般的周期信号频谱特点相同

（2）周期矩形脉冲信号的频谱也是离散的，它仅含有(omega_0 = 2pi/T)的主频率分量，相邻谱线间的距离为(omega_0 = frac{2pi}{T})

（3）显然，当周期T变大时，谱线间隔(omega_0)变小，频谱变得 稠密；反之则稀疏。

（4）无论谱线变稠密还是变稀疏，频谱的形状亦及其包络不随T的变换而变化，在(omegatau/2 = mpi)处，各频率分量为零。

（5）由于各分量的幅值随频率的增加而减小，因此信号的能量主要集中在第一个零点，即(omega = 2pi/tau)以内。

（6）在允许一定误差的条件下，通常将(0leqomegaleq 2pi/tau)这段频率范围称为周期矩形脉冲信号的带宽，用符号(Delta C)表示：(Delta C = 1/tau)

3. 周期矩形脉冲信号的周期和脉宽

（1）周期相同，脉宽不同

由于信号的周期相同，因而信号的谱线间隔相同。

由式(Delta C = 1/tau)可知，脉冲宽度越窄，信号的带宽远大，宠儿使得频带中包含的频率分量越多。另外，当信号周期不变而脉宽减小时，由下式可知信号的频谱幅值也减小。

(x(t) = frac{tau}{T}sum_{-infty}^{infty}sinc(frac{npitau}{T})e^{jnomega_0t})

 

（2）脉宽相同，周期不同

由于脉宽相同，因而带宽相同。(Delta C = 1/tau)

当周期变大时，信号谱线的间隔便减小。

若周期无限增大，则周期信号变成非周期信号。此时，谱线变得越来越密集，最终谱线间隔趋近于零，整个谱线便成为一条连续的频谱。

同样，由Fourier变换表达式可知，当周期增大而脉宽不变时，各频率分量幅值相应变小。

 

4. 周期性矩形脉冲信号的频谱特征

考虑当周期矩形脉冲信号的周期T和脉宽(tau)改变时它们的频谱变化的情形。

（1）当(tau)不变，改变T时，随着T的增大，占空比减小。

谱线间隔变小，幅度下降。

但频谱包络的形状不变，包络主瓣内包含的鞋包分量数增加。

（2）当(tau)改变，T不变时，随着(tau)减小使占空比减小。

谱线间隔不变，幅度下降。

频谱的包络改变，包络主瓣变宽。主瓣呢你包含的谐波数量也增加。

三、吉伯斯现象

当用Fourier级数的谐波分量之和表示具有间断点的波形时，由于展开式在间断点邻域不能均匀收敛，会引起吉伯斯现象，即使当N趋于无穷，这一现象依然存在。

 

1. 吉伯斯现象基本介绍

实际中，傅里叶有限级数n = N，N是有限整数。

当采用有限项级数之和重现原波形时，所取项数越多，其合成波形越接近原波形。

N增大时，波形顶部逐渐趋于平坦，跳变峰向间断点靠近，跳变峰所包面积减小。

N很大时，跳变峰所包含的面积趋于0，跳变峰高度将趋于间断点处幅值的0.08948

2. 吉伯斯现象的启示

吉伯斯现象还表明

信号中的低频分量影响了脉冲的顶部

信号中的高频分量影响了间断点处的波形

因此给我们带来了如下启示：

（1）当从时域观察一个信号时，从波形变化的缓急程度可以看出所包含频率的成分

（2）变化平缓的信号：频带越窄，包含的频率成分越少

（3）变化越快的信号：频带越宽，包含的频率成分越多

3. 吉伯斯现象的意义

研究滤波器即窗函数的数学基础。

它表明：

用有限项傅里叶级数表示有间断点的信号时，在间断点附近不可避免的会出现震荡和超量，超量的幅度不会随所取项目的增加而减小，只是随着项数的增多，振荡频率变高，并向间断点处压缩，从而它占有的能量减少。

4. 离散时间周期信号的Fourier级数

DFS是一个有限项的级数，确定的关系式也是有限项的和式，因而不存在收敛问题，也不会产生Gibbs现象。

四、周期信号的功率

1. 周期信号的功率

(x(t) = frac{a_0}{2} + sum_{n = 1}^{infty}A_ncos(nomega_0t + phi_0))

则x(t)的功率为：

(P = frac{1}{T}int_{-T/2}^{T/2}x^(t)dt)

(P = frac{1}{T}int_{-T/2}^{T/2}[frac{a_0}{2} + sum_{n = 1}^{infty}A_ncos(nomega_0t + phi_0)]^2dt)

(P = (frac{a_0}{2})^2 + sum_{n = 1}^{infty}frac{1}{2}A_n^2)

上式等号右端的第一项表示信号x(t)的直流功率，而第二项则为信号的各次谐波的功率之和。

2. Parserval定理

周期信号在时域中的信号功率等于信号在频域中的功率。

(P = (frac{a_0}{2})^2 + sum_{n = 1}^{infty}frac{1}{2}A_n^2)

(P = sum_{n = -infty}^{infty}|C_n|^2)

3. 周期信号的功率谱

定义周期信号x(t)的功率谱为

(P_n = |C_n|^2, n = 0, pm 1, pm 2, cdots)

功率谱的性质：

非负数，偶函数，不随着时移(tau)而改变

可以定义(p_n = sqrt{P_n})

(C_n = sqrt{P_n}e^{jphi_n})

五、非周期信号的频域描述

傅里叶变换

(X(omega) = int_{-infty}^{infty}x(t)e^{-jomega t}dt)

傅里叶逆变换

(x(t) = frac{1}{2pi}int_{-infty}^{infty}X(omega)e^{jomega t}domega)

1. 非周期函数的傅里叶变换

非周期函数x(t)存在傅里叶变换的充分条件是x(t)在区间((-infty), infty)上绝对可积

(int_{-infty}^{infty}|x(t)|^2dt < infty)

但上述条件并非必要条件，引入广义函数后许多不满足绝对可积条件的函数也能进行fourier变换。

2. 非周期函数的频谱

（1）周期信号的幅值谱(|C_n|)与信号幅值量纲一致

（2）非周期信号的(|X(f)|)的量纲与信号幅值量纲不一致

x(t)与(X(f)df)的两个是一致的，所以严格的说，X(f)是频谱密度函数

3. 非周期信号的能量

一个非周期函数x(t)的能量为

(E = int_{-infty}^{infty}x^2(t)dt = frac{1}{2pi}int_{-infty}^{infty}|X(omega)|^2domega)

这个式子也称为巴塞伐尔方程或能量等式

4. 能量谱

(E = frac{1}{2pi}int_{-infty}^{infty}|X(omega)|^2domega)

( = frac{1}{pi}int_{0}^{infty}|X(omega)|^2domega)

( = int_{0}^{infty}S(omega)domega)

(S(omega) = |X(omega)|^2/pi)

其中(S(omega))称为x(t)的能量谱密度函数，简称能量谱函数。

（1）信号的能量谱是偶函数，仅取决于频谱函数的模，与相位无关

（2）周期信号中每个谐波分量与一定量的功率可以相互联系起来；同样，能量信号中的能量同连续的频带也可以联系起来。

六、Fourier变换的性质

这里仅列举几个重要的

(x(t)leftrightarrow X(omega))

1. 对称性

(X(t)leftrightarrow 2pi x(-omega))

2. 尺度变换性

(x(at) leftrightarrow frac{1}{|a|}X(frac{omega}{a}))

若信号x(t)在时间轴上被压缩至原信号的1/a，则其频谱函数在频率轴上将展宽a倍，而其幅值相应地减至原信号幅值的1/|a|。信号的持续时间与信号占有的频带宽成反比。

3. 时移性

(x(t - t_0) leftrightarrow X(omega)e^{-jomega t_0})

4. 频移性（调制性）

(x(t)e^{jomega t_0} leftrightarrow X(omega - omega_0))

 

5. 卷积

定义

(x(t) * h(t) = int_{-infty}^{infty}x(tau) cdot h(t - tau)dtau)

时域卷积

(x(t) * h(t) leftrightarrow X(omega)cdot H(omega))

频域卷积

(x(t)cdot h(t) leftrightarrow frac{1}{2pi}X(omega)*H(omega))

6. 时域微分和积分

(frac{dx(t)}{dt} leftrightarrow jomega X(omega))

(int_{-infty}^{t}x(t)dt leftrightarrow frac{1}{jomega} X(omega))

7. 频域微分和积分

(-jtx(t) leftrightarrow frac{dX(omega)}{domega})

(pi x(0)delta(t) + frac{1}{-jt}x(t) leftrightarrow int_{-infty}^{infty}X(omega)domega)

七、功率信号的fourier变换

在前面研究fourier变换存在的条件时曾指出，并非所有的韩寒诉均具有fourier变换，只有那些满足狄里赫利条件的信号才具有fourier变换。常见的能量信号均满足此条件，即他们在区间负无穷到正无穷是可积的。

然而，有些十分有用的信号如正弦函数，单位阶跃函数等却不是绝对可积的，但是可以利用单位脉冲函数和某些高阶的奇异函数的傅里叶变换来实现这些函数的傅里叶变换

上述这一类信号称为功率信号，即前面所提到的有限平均功率信号，它们在((-infty, infty))区域上的能量可能趋近于无穷，但它们的功率是有限的，即满足

(P = lim_{Trightarrowinfty}frac{1}{T}int_{-T/2}^{T/2}x^2(t)dt < infty)

1. 单位脉冲函数

性质

（1）(int_{-infty}^{infty}x(t)delta(t - t_0)dt = x(t_0))

（2）(X(omega) = F[delta(t)] = 1)

（3）(delta(t - t_0) leftrightarrow e^{-jomega t_0})

(e^{jomega_0t leftrightarrow 2pidelta(omega - omega_0)})

(1 leftrightarrow 2pidelta(omega))

2. 余弦函数

欧拉公式：(cosomega_0t = frac{e^{jomega_0t} + e^{-jomega_0t}}{2})

余弦函数的频谱：(cosomega_0t leftrightarrow pi[delta(omega - omega_0) + delta(omega + omega_0)])

正弦函数的频谱：(sinomega_0t leftrightarrow jpi[delta(omega + omega_0) - delta(omega + omega_0)])

 

3. 符号函数

(sgn(t) leftrightarrow frac{2}{jomega})

 

4. 单位阶跃函数

(xi(t) = 1/2 + sgn(t)/2)

(F[xi(t)] = F[1/2] + F[sgn(t)/2] = pidelta(omega) + 1/jomega)

5. 周期函数

(x(t) = sum_{n = -infty}^{infty}C_ne^{jnomega_0t})

(C_n = frac{1}{T}int_{-T/2}^{T/2}x(t)e^{-jnomega_0t}dt)

x(t)的Fourier变换为

(X(omega) = 2pisum_{n = -infty}^{infty}C_ndelta(omega - nomega_0))

即一个周期函数的傅里叶变换由无穷多个位于 x(t)各谐波频率上的单位脉冲函数组成。

6. 周期脉冲序列的Fourier变换

(x(t) = sum_{k = -infty}^{infty}delta(t - kT))

(C_n = frac{1}{T}int_{-T/2}^{T/2}delta(t)e^{-jnomega_0t}dt = frac{1}{T})

(X(omega) = frac{2pi}{T}sum_{n = -infty}^{infty}delta(omega - nomega_0), omega_0 = frac{2pi}{T})

 

一个周期脉冲序列的傅里叶变换仍为一个周期脉冲序列