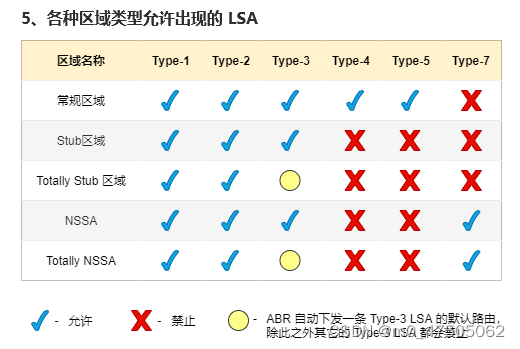
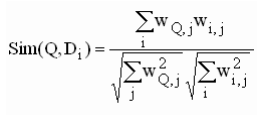LSA潜在语义分析

【转自：https://blog.csdn.net/roger__wong/article/details/41175967】

原文地址：http://en.wikipedia.org/wiki/Latent_semantic_analysis

前言

浅层语义分析（LSA）是一种自然语言处理中用到的方法，其通过“矢量语义空间”来提取文档与词中的“概念”，进而分析文档与词之间的关系。LSA的基本假设是，如果两个词多次出现在同一文档中，则这两个词在语义上具有相似性。LSA使用大量的文本上构建一个矩阵，这个矩阵的一行代表一个词，一列代表一个文档，矩阵元素代表该词在该文档中出现的次数，然后再此矩阵上使用奇异值分解（SVD）来保留列信息的情况下减少矩阵行数，之后每两个词语的相似性则可以通过其行向量的cos值（或者归一化之后使用向量点乘）来进行标示，此值越接近于1则说明两个词语越相似，越接近于0则说明越不相似。

LSA最早在1988年由 Scott Deerwester, Susan Dumais, George Furnas, Richard Harshman, Thomas Landauer, Karen Lochbaum and Lynn Streeter提出，在某些情况下，LSA又被称作潜在语义索引（LSI）。

概述

词-文档矩阵（Occurences Matrix)

LSA 使用词-文档矩阵来描述一个词语是否在一篇文档中。词-文档矩阵式一个稀疏矩阵，其行代表词语，其列代表文档。一般情况下，词-文档矩阵的元素是该词在文档中的出现次数，也可以是是该词语的tf-idf(term frequency–inverse document frequency)。

词-文档矩阵和传统的语义模型相比并没有实质上的区别，只是因为传统的语义模型并不是使用“矩阵”这种数学语言来进行描述。

降维

在构建好词-文档矩阵之后，LSA将对该矩阵进行降维，来找到词-文档矩阵的一个低阶近似。降维的原因有以下几点：

原始的词-文档矩阵太大导致计算机无法处理，从此角度来看，降维后的新矩阵式原有矩阵的一个近似。
原始的词-文档矩阵中有噪音，从此角度来看，降维后的新矩阵式原矩阵的一个去噪矩阵。
原始的词-文档矩阵过于稀疏。原始的词-文档矩阵精确的反映了每个词是否“出现”于某篇文档的情况，然而我们往往对某篇文档“相关”的所有词更感兴趣，因此我们需要发掘一个词的各种同义词的情况。

降维的结果是不同的词或因为其语义的相关性导致合并，如：

{(car), (truck), (flower)} --> {(1.3452 * car + 0.2828 * truck), (flower)}

将维可以解决一部分同义词的问题，也能解决一部分二义性问题。具体来说，原始词-文档矩阵经过降维处理后，原有词向量对应的二义部分会加到和其语义相似的词上，而剩余部分则减少对应的二义分量。

推导

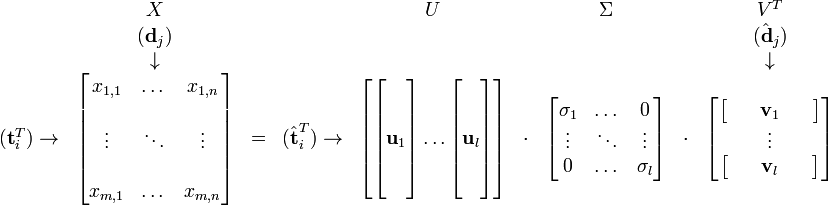
假设X是词-文档矩阵，其元素（i,j）代表词语i在文档j中的出现次数，则X矩阵看上去是如下的样子：

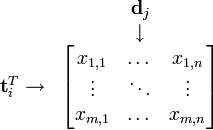
$\begin{matrix} & \textbf{d}_j \\ & \downarrow \\\textbf{t}_i^T \rightarrow &\begin{bmatrix} x_{1,1} & \dots & x_{1,n} \\\vdots & \ddots & \vdots \\x_{m,1} & \dots & x_{m,n} \\\end{bmatrix}\end{matrix}$

可以看到，每一行代表一个词的向量，该向量描述了该词和所有文档的关系。

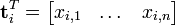
$\textbf{t}_i^T = \begin{bmatrix} x_{i,1} & \dots & x_{i,n} \end{bmatrix}$

相似的，一列代表一个文档向量，该向量描述了该文档与所有词的关系。

$\textbf{d}_j = \begin{bmatrix} x_{1,j} \\ \vdots \\ x_{m,j} \end{bmatrix}$

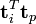词向量 $\textbf{t}_i^T \textbf{t}_p$ 的点乘可以表示这两个单词在文档集合中的相似性。矩阵 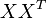$X X^T$ 包含所有词向量点乘的结果，元素（i,p）和元素（p,i）具有相同的值，代表词p和词i的相似度。类似的，矩阵 $X^T X$ 包含所有文档向量点乘的结果，也就包含了所有文档那个的相似度。

现在假设存在矩阵 $X$ 的一个分解，即矩阵 $X$ 可分解成正交矩阵U和V，和对角矩阵 $\Sigma$ 的乘积。

这种分解叫做奇异值分解（SVD），即：

$\begin{matrix}X = U \Sigma V^T\end{matrix}$

因此，词与文本的相关性矩阵可以表示为：

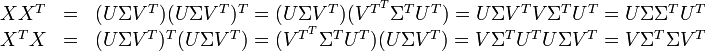
$\begin{matrix}X X^T &=& (U \Sigma V^T) (U \Sigma V^T)^T = (U \Sigma V^T) (V^{T^T} \Sigma^T U^T) = U \Sigma V^T V \Sigma^T U^T = U \Sigma \Sigma^T U^T \\X^T X &=& (U \Sigma V^T)^T (U \Sigma V^T) = (V^{T^T} \Sigma^T U^T) (U \Sigma V^T) = V \Sigma^T U^T U \Sigma V^T = V \Sigma^T \Sigma V^T\end{matrix}$

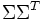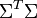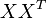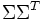因为 $\Sigma \Sigma^T$ 与 $\Sigma^T \Sigma$ 是对角矩阵，因此 $U$ 肯定是由 $X X^T$ 的特征向量组成的矩阵，同理 $V$ 是 $X^T X$ 特征向量组成的矩阵。这些特征向量对应的特征值即为 $\Sigma \Sigma^T$ 中的元素。综上所述，这个分解看起来是如下的样子：

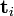$\begin{matrix} & X & & & U & & \Sigma & & V^T \\ & (\textbf{d}_j) & & & & & & & (\hat{\textbf{d}}_j) \\ & \downarrow & & & & & & & \downarrow \\(\textbf{t}_i^T) \rightarrow &\begin{bmatrix} x_{1,1} & \dots & x_{1,n} \\\\\vdots & \ddots & \vdots \\\\x_{m,1} & \dots & x_{m,n} \\\end{bmatrix}&=&(\hat{\textbf{t}}_i^T) \rightarrow&\begin{bmatrix} \begin{bmatrix} \, \\ \, \\ \textbf{u}_1 \\ \, \\ \,\end{bmatrix} \dots\begin{bmatrix} \, \\ \, \\ \textbf{u}_l \\ \, \\ \, \end{bmatrix}\end{bmatrix}&\cdot&\begin{bmatrix} \sigma_1 & \dots & 0 \\\vdots & \ddots & \vdots \\0 & \dots & \sigma_l \\\end{bmatrix}&\cdot&\begin{bmatrix} \begin{bmatrix} & & \textbf{v}_1 & & \end{bmatrix} \\\vdots \\\begin{bmatrix} & & \textbf{v}_l & & \end{bmatrix}\end{bmatrix}\end{matrix}$

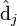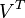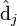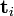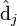$\sigma_1, \dots, \sigma_l$ 被称作是奇异值，而 $u_1, \dots, u_l$ 和 $v_1, \dots, v_l$ 则叫做左奇异向量和右奇异向量。通过矩阵分解可以看出，原始矩阵中的 $\textbf{t}_i$ 只与U矩阵的第i行有关，我们则称第i行为 $\hat{\textrm{t}}_i$ 。同理，原始矩阵中的 $\hat{ \textrm{d}}_j$ 只与 $V^T$ 中的第j列有关，我们称这一列为 $\hat{ \textrm{d}}_j$ 。 $\textbf{t}_i$ 与 $\hat{ \textrm{d}}_j$ 并非特征值，但是其由矩阵所有的特征值所决定。

当我们选择k个最大的奇异值，和它们对应的Ｕ与Ｖ中的向量相乘，则能得到一个X矩阵的k阶近似，此时该矩阵和X矩阵相比有着最小误差（即残差矩阵的Frobenius范数）。但更有意义的是这么做可以将词向量和文档向量映射到语义空间。向量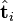 $\hat{\textbf{t}}_i$ 与含有k个奇异值的矩阵相乘，实质是从高维空间到低维空间的一个变换，可以理解为是一个高维空间到低维空间的近似。同理，向量 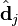$\hat{\textbf{d}}_j$ 也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子：

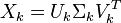
$X_k = U_k \Sigma_k V_k^T$

有了这个变换，则可以做以下事情：

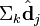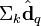判断文档 $j$ 与 $q$ 在低维空间的相似度。比较向量 $\Sigma_k \hat{\textbf{d}}_j$ 与向量 $\Sigma_k \hat{\textbf{d}}_q$ (比如使用余弦夹角)即可得出。
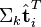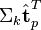通过比较 $\Sigma_k \hat{\textbf{t}}_i^T$ 与 $\Sigma_k \hat{\textbf{t}}_p^T$ 可以判断词 $i$ 和词 $p$ 的相似度。
有了相似度则可以对文本和文档进行聚类。
给定一个查询字符串，算其在语义空间内和已有文档的相似性。

要比较查询字符串与已有文档的相似性，需要把文档和查询字符串都映射到语义空间，对于原始文档，由以下公式可以进行映射：

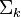$\hat{\textbf{d}}_j = \Sigma_k^{-1} U_k^T \textbf{d}_j$

其中对角矩阵 $\Sigma_k$ 的逆矩阵可以通过求其中非零元素的倒数来简单的得到。

同理，对于查询字符串，得到其对应词的向量后，根据公式 $\hat{\textbf{q}} = \Sigma_k^{-1} U_k^T \textbf{q}$ 将其映射到语义空间，再与文档进行比较。

应用

低维的语义空间可以用于以下几个方面:

在低维语义空间可对文档进行比较，进而可用于文档聚类和文档分类。
在翻译好的文档上进行训练，可以发现不同语言的相似文档，可用于跨语言检索。
发现词与词之间的关系，可用于同义词、歧义词检测。.
通过查询映射到语义空间，可进行信息检索。
从语义的角度发现词语的相关性，可用于“选择题回答模型”（multi choice qustions answering model）。

（原文还说了一些其它方面，感觉不是很重要，不翻译了，放上原文）

Synonymy and polysemy are fundamental problems in natural language processing:

Synonymy is the phenomenon where different words describe the same idea. Thus, a query in a search engine may fail to retrieve a relevant document that does not contain the words which appeared in the query. For example, a search for "doctors" may not return a document containing the word "physicians", even though the words have the same meaning.
Polysemy is the phenomenon where the same word has multiple meanings. So a search may retrieve irrelevant documents containing the desired words in the wrong meaning. For example, a botanist and a computer scientist looking for the word "tree" probably desire different sets of documents.

Commercial applications[edit]

LSA has been used to assist in performing prior art searches for patents.[5]

Applications in human memory[edit]

The use of Latent Semantic Analysis has been prevalent in the study of human memory, especially in areas of free recall and memory search. There is a positive correlation between the semantic similarity of two words (as measured by LSA) and the probability that the words would be recalled one after another in free recall tasks using study lists of random common nouns. They also noted that in these situations, the inter-response time between the similar words was much quicker than between dissimilar words. These findings are referred to as the Semantic Proximity Effect.[6]

When participants made mistakes in recalling studied items, these mistakes tended to be items that were more semantically related to the desired item and found in a previously studied list. These prior-list intrusions, as they have come to be called, seem to compete with items on the current list for recall.[7]

Another model, termed Word Association Spaces (WAS) is also used in memory studies by collecting free association data from a series of experiments and which includes measures of word relatedness for over 72,000 distinct word pairs.[8]

算法局限性

LSA的一些缺点如下:

新生成的矩阵的解释性比较差.比如

{(car), (truck), (flower)} ↦ {(1.3452 * car + 0.2828 * truck), (flower)}

(1.3452 * car + 0.2828 * truck) 可以解释成 "vehicle"。同时，也有如下的变换

{(car), (bottle), (flower)} ↦ {(1.3452 * car + 0.2828 * bottle), (flower)}

造成这种难以解释的结果是因为SVD只是一种数学变换，并无法对应成现实中的概念。

LSA无法扑捉一词多以的现象。在原始词-向量矩阵中，每个文档的每个词只能有一个含义。比如同一篇文章中的“The Chair of Board"和"the chair maker"的chair会被认为一样。在语义空间中，含有一词多意现象的词其向量会呈现多个语义的平均。相应的，如果有其中一个含义出现的特别频繁，则语义向量会向其倾斜。