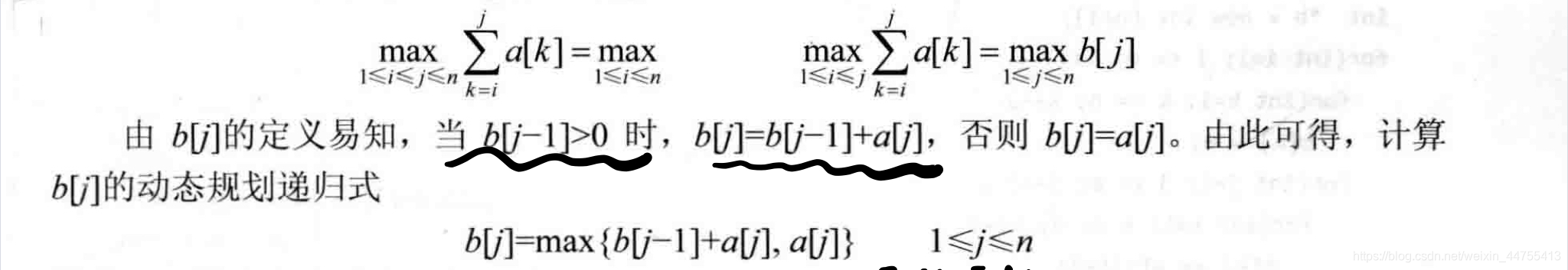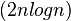2018-01-14 21:14:58
一、最大子段和问题
问题描述:给定n个整数(可能有负数)组成的序列a1,a2,...,an,求该序列的最大子段和。如果所有整数都是负数,那么定义其最大子段和为0。
方法一、最大子段和的简单算法
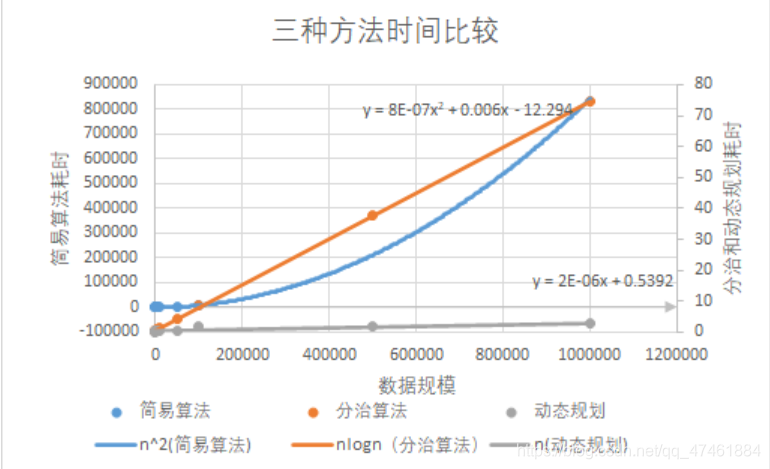
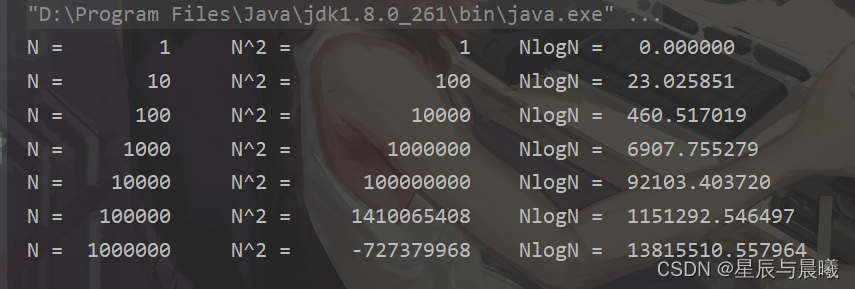
显然可以在O(n^2)的时间复杂度上完成这个问题。但是是否可以对算法进行优化呢?答案是肯定的。
方法二、分治算法
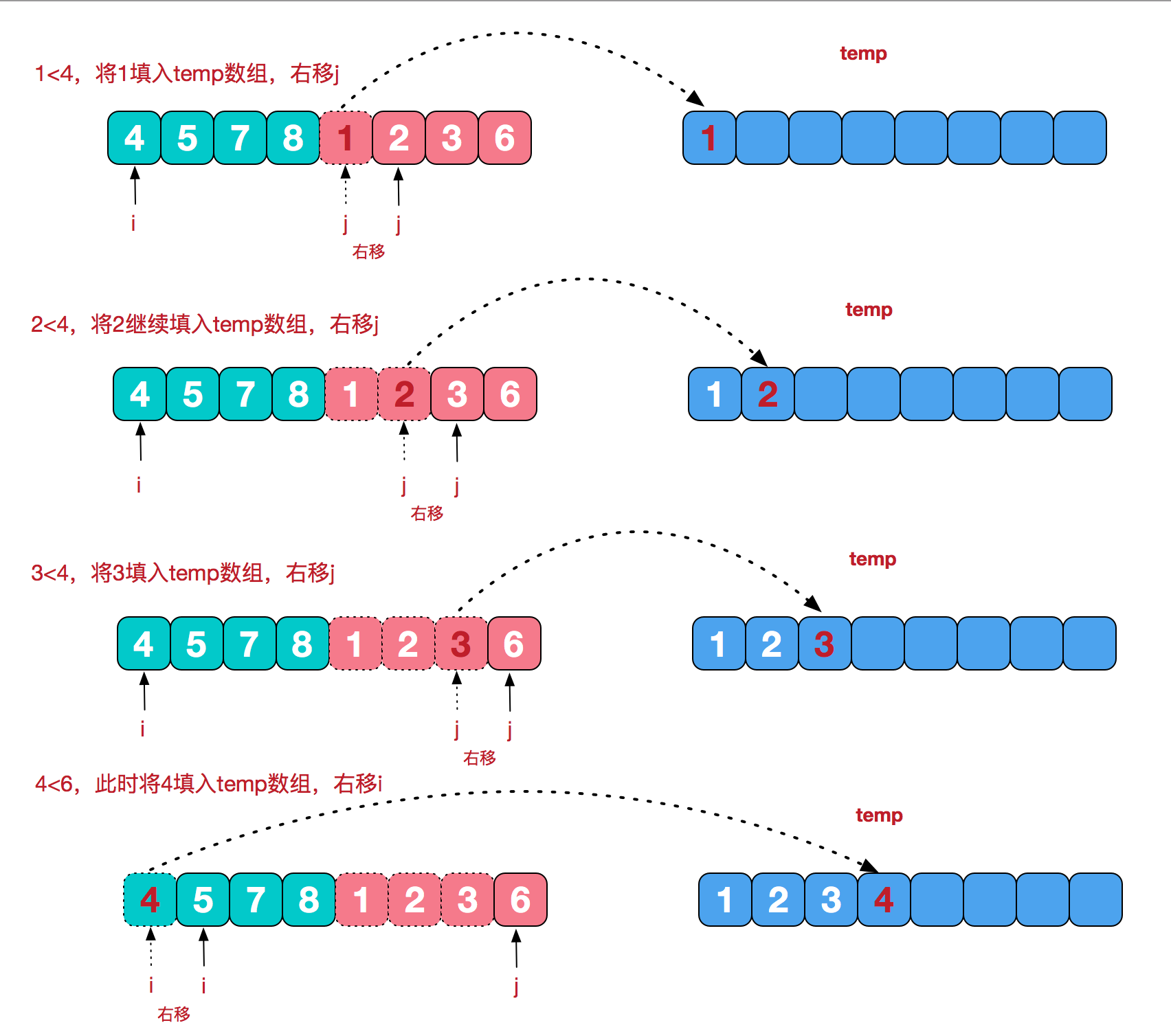
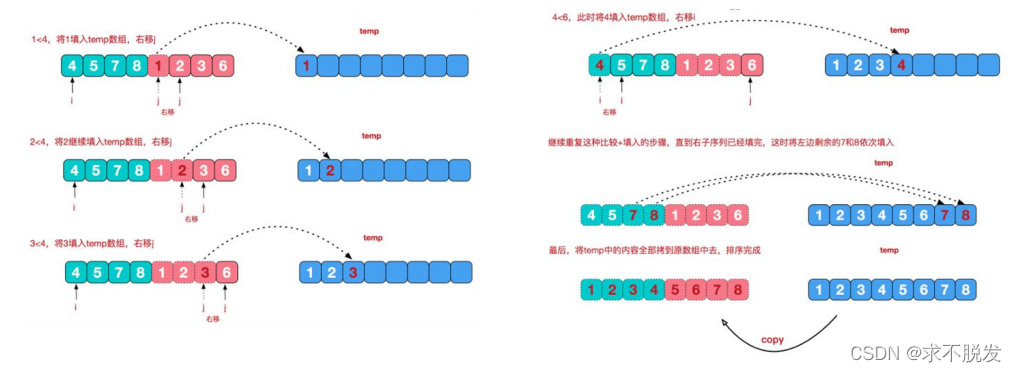
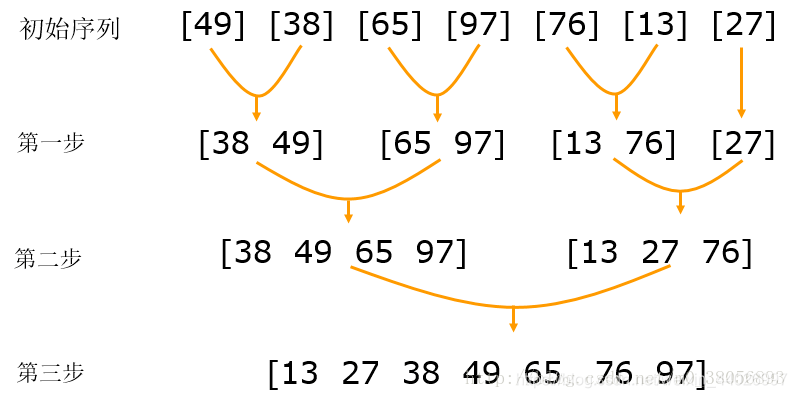
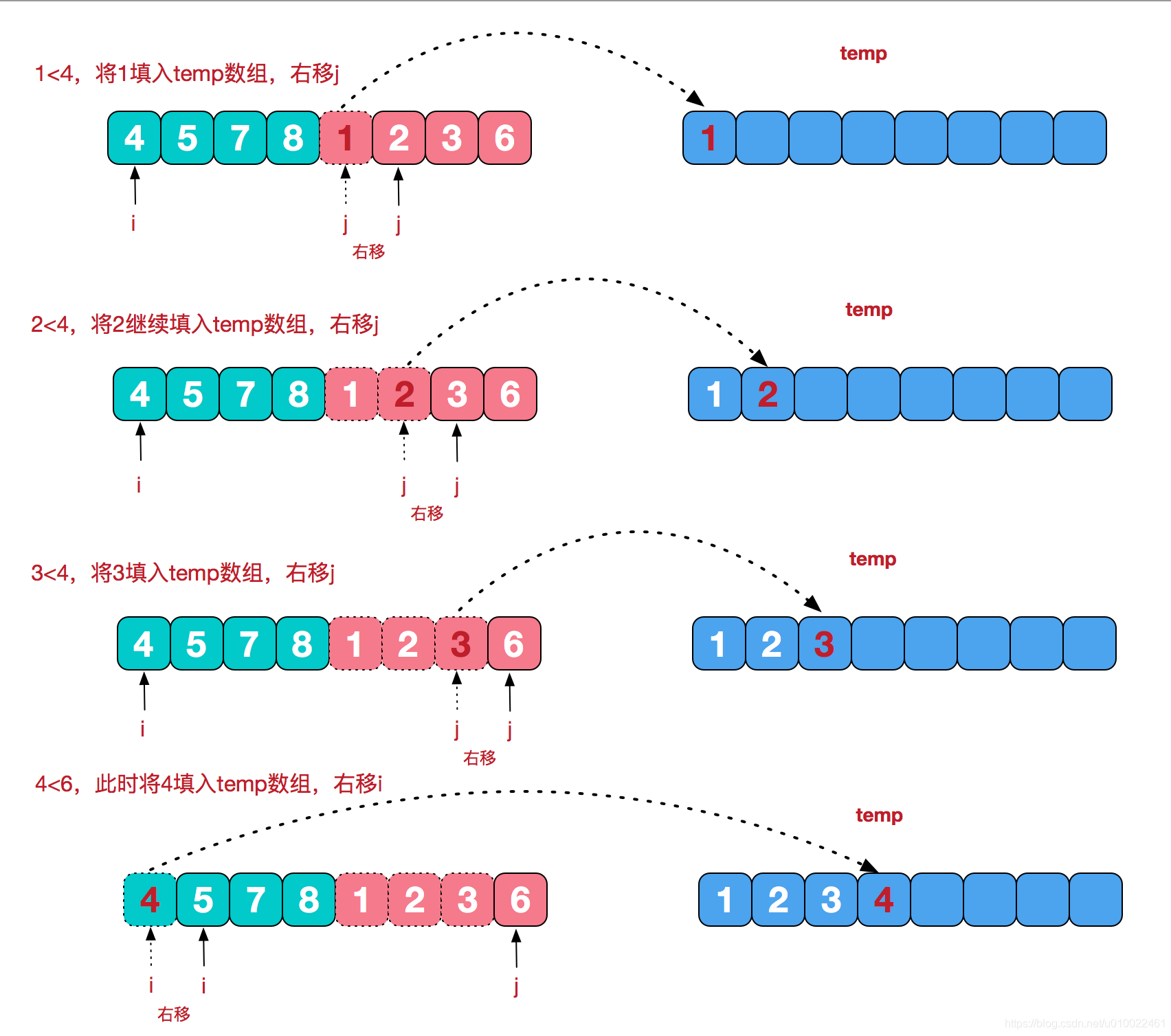
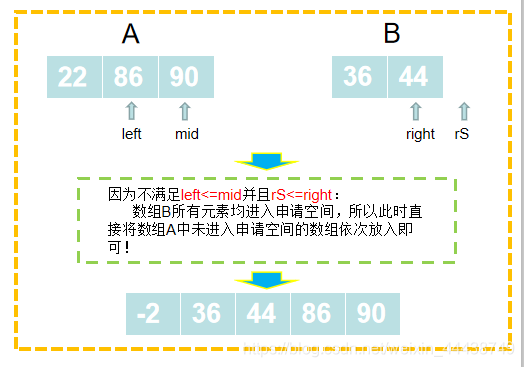
朴素的分法是二分,问题就是如何merge,在merge的时候,因为已经确定了会包含边界点,所以可以在O(n)的时间复杂度上完成merge时的最大子段和。
因此分治公式是:T(n) = 2T(n/2)+O(n)
根据主定理可以算得,分治算法的时间复杂度为O(nlgn)。
int maxSubSum(int[] a,int L,int R){
if(L == R) return a[L] > 0 ? a[L] : 0;
else {
int mid = L + (R - L) / 2;
int sumL = maxSubSum(a, L, mid);
int sumR = maxSubSum(a, mid + 1, R);
int tmpL = 0;
int tmpR = 0;
int sum = 0;
for (int i = mid; i >=0 ; i--) {
sum += a[i];
if(sum>tmpL) tmpL = sum;
}
sum = 0;
for (int i = mid+1; i <=R ; i++) {
sum += a[i];
if(sum>tmpR) tmpR = sum;
}
return Math.max(sumL,Math.max(sumR,tmpL+tmpR));
}
}
方法三、动态规划

这种两端都是变化的问题是很难优化的,最好可以让一端固定,这样就会大大简化分析难度。于是将j暂时从原式子中提取出来,将剩下的命名为b[j]。
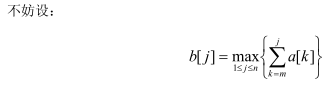
所以原问题就变成了这样。

根据b[j]的定义,b[j]是指以a[j]结尾的最大子段和。因此有如下公式:
b[j] = max{b[j - 1] + a[j] , a[j]} 1=
有了b[j],再对他取个极值,就可以得到原问题的解。
时间复杂度为O(n)
int maxSum(int[] a) {
int res = 0;
int b = 0;
for (int i = 0; i < a.length; i++) {
b = Math.max(b + a[i], a[i]);
if (b > res) res = b;
}
return res;
}
二、推广问题
最大子矩阵和问题
问题描述:给定一个m*n的整数矩阵A,试求矩阵A的一个子矩阵,使其各个元素之和最大。
问题分析:事实上,只需要将矩阵“压扁”就可以规约到最大子段和问题,具体来说就是将多行进行求和变为一行,这样就可以直接使用上述问题的解法。将多行“压缩”成一行有多种可行方案,需要遍历一下,花费O(m^2),最大子段和动态规划算法花费O(n),所以总的时间消耗是O(m^2*n)。
最大m子段和问题
问题描述:给定n个整数(可能有负数)组成的序列a1,a2,...,an,以及一个正整数m,要求确定该序列的m个不相交子段,使这m个子段的总和最大。
问题分析:设b(i, j)表示数组a的前j项中i个子段和的最大值,且第i个子段含a[j](1<=i<=m,i<=j<=n),则所求的最优值显然为max b(m, j),其中 m <= j <= n。
与最大子段和类似。计算b(i,j)的递归式子为:
b(i, j) = max{ b(i, j-1) + a[j] , max{ b(i - 1, t) + a[j] 其中t = i - 1 ~ j - 1} }
初始时,b(0, j) = 0; b(i, 0) = 0。
#include "stdafx.h"
#include
using namespace std;
int MaxSum(int m,int n,int *a);
int main() {
int a[] = {0,2,3,-7,6,4,-5};//数组脚标从1开始
for(int i=1; i<=6; i++) {
cout<
}
cout<
cout<
}
int MaxSum(int m,int n,int *a) {
if(n
return 0;
int **b = new int *[m+1];
for(int i=0; i<=m; i++) {
b[i] = new int[n+1];
}
for(int i=0; i<=m; i++) {
b[i][0] = 0;
}
for(int j=1;j<=n; j++) {
b[0][j] = 0;
}
//枚举子段数目,从1开始,迭代到m,递推出b[i][j]的值
for(int i=1; i<=m; i++) {
//n-m+i限制避免多余运算,当i=m时,j最大为n,可据此递推所有情形
for(int j=i; j<=n-m+i; j++) {
if(j>i) {
b[i][j] = b[i][j-1] + a[j];//代表a[j]同a[j-1]一起,都在最后一子段中
for(int k=i-1; k
if(b[i][j]
b[i][j] = b[i-1][k]+a[j];//代表最后一子段仅包含a[j]
}
}
else {
b[i][j] = b[i-1][j-1]+a[j];//当i=j时,每一项为一子段
}
}
}
int sum = 0;
for(int j=m; j<=n; j++) {
if(sum
sum = b[m][j];
}
}
return sum;
}
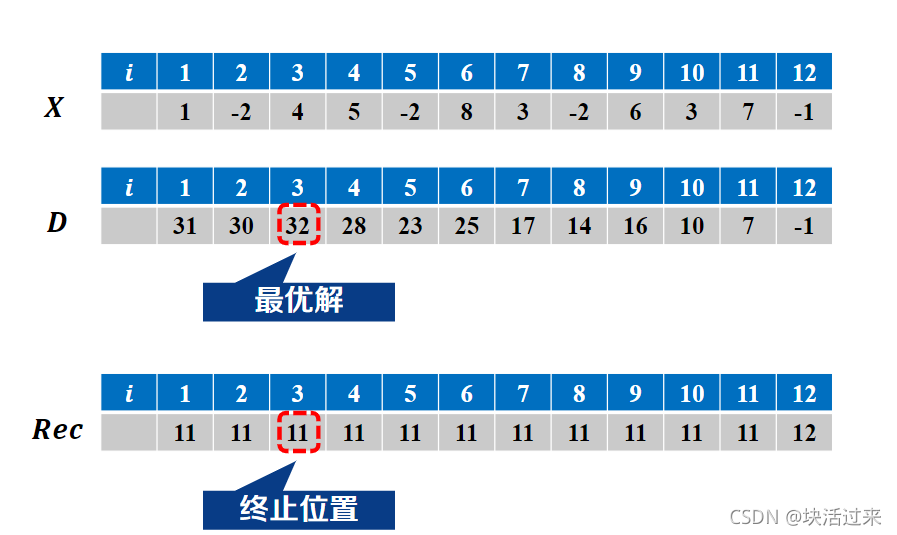
上述算法显然需要O(m*n^2)计算时间和O(m*n)。可以看一下具体矩阵是怎么填写的。
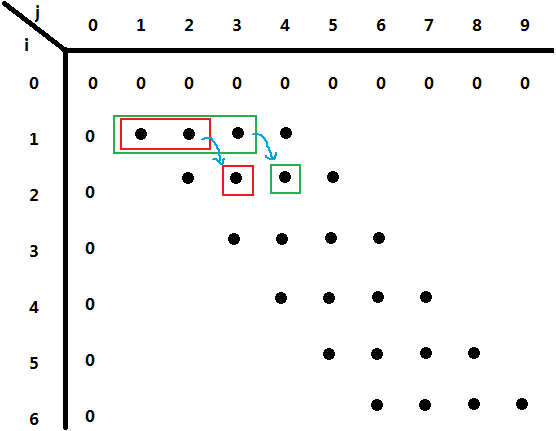
注意到上述算法中,计算b[i][j]时只用到了b的当前行的前一个数以及上一行的一个极值。因此我们可以定义两个数组,一个数组来保存当前行,一个数组来保存上一行的极值。并且使用数组来保存极值可以边生成当前行的数值边进行极值的判断并进行填充。
#include "stdafx.h"
#include
using namespace std;
int MaxSum(int m,int n,int *a);
int main() {
int a[] = {0,2,3,-7,6,4,-5};//数组脚标从1开始
for(int i=1; i<=6; i++) {
cout<