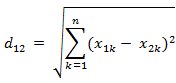参考 常见向量范数和矩阵范数及其MATLAB实现 - 云+社区 - 腾讯云
1、向量范数
1-范数: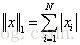
2-范数: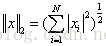
∞-范数: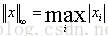
-∞-范数: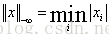
p-范数: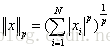
2、矩阵范数
1-范数: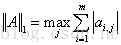
2-范数: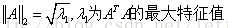
∞-范数: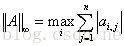
F-范数: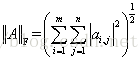
下面是解释和理解。
1-范数(列和范数)
将矩阵沿列方向取绝对值求和,然后擢选出数值最大的那个值作为1-范数。
比如:
A =1 2 34 5 67 8 9>> norm_1 = norm(A,1)norm_1 =18
第一列求和结果为:|1|+|4|+|7|=12
第二列求和结果为:|2|+|5|+|8|=15
第三列求和结果为:|3|+|6|+|9|=18
里面最大的就是18,因此矩阵A的列和范数为18。
2-范数(最大特征值开方)
这一部分涉及到的我不懂的概念比较多,接下来一一说明。
2-1 共轭转置矩阵
指的是A的共轭转置矩阵,也有这个写法。如果A里面全是实数,那效果就与无二;如果A里面也有复数,则是先对A取共轭(各项实部不变,虚部取相反数),然后再转置,比如:
A =1.0000 + 0.0000i 0.0000 - 2.0000i3.0000 + 0.0000i 0.0000 - 4.0000i>> A'ans =1.0000 + 0.0000i 3.0000 + 0.0000i0.0000 + 2.0000i 0.0000 + 4.0000i在matlab中A’的意思就是求共轭转置矩阵。
2-2 特征值
矩阵A的特征值被定义为:
其中被称为“矩阵A的特征向量”,λ被称为“矩阵A的特征值”。
在matlab中求解矩阵A的特征值方法如下:
A =1 2 34 5 67 8 9>> [V,D] = eig(A)V =-0.2320 -0.7858 0.4082-0.5253 -0.0868 -0.8165-0.8187 0.6123 0.4082D =16.1168 0 00 -1.1168 00 0 -0.0000
矩阵V的每一列都是一个特征向量,D中对应列中的值即与该特征向量相匹配的特征值。以上例V、D第一列为例,此时特征值λ=16.1168,特征向量,用matlab作验证如下:
>> A = [1,2,3;4,5,6;7,8,9]A =1 2 34 5 67 8 9>> v = [-0.2320,-0.5253,-0.8187]'
v =-0.2320-0.5253-0.8187
>> lambda = 16.1168
lambda =16.1168
>> A * v
ans =-3.7387-8.4667-13.1947
>> lambda * v
ans =-3.7391-8.4662-13.1948
可知满足。
2-3 矩阵的2-范数
矩阵的2-范数即对矩阵最大特征值开方,如下:
>> [V,D] = eig(A'*A)V =-0.4082 -0.7767 0.47970.8165 -0.0757 0.5724-0.4082 0.6253 0.6651D =0.0000 0 00 1.1414 00 0 283.8586>> sqrt(283.8586)ans =16.8481(这里最大特征值为283.8586)
当然,matlab中也有更直接的计算矩阵2-范数的方法,如下:
>> norm_2 = norm(A,2)
norm_2 =16.8481
两种方法计算出的结果是一样的。
∞-范数(行和范数)
和1-范数(列和范数)类似,这里是沿行方向取绝对值求和,将最大的那个值作为矩阵的∞-范数。matlab代码如下:
>> AA =1 2 34 5 67 8 9>> norm(A,inf)ans =24第一行求和结果为:|1|+|2|+|3|=6
第二行求和结果为:|4|+|5|+|6|=15
第三行求和结果为:|7|+|8|+|9|=24
里面最大的就是24,因此矩阵A的行和范数为24。