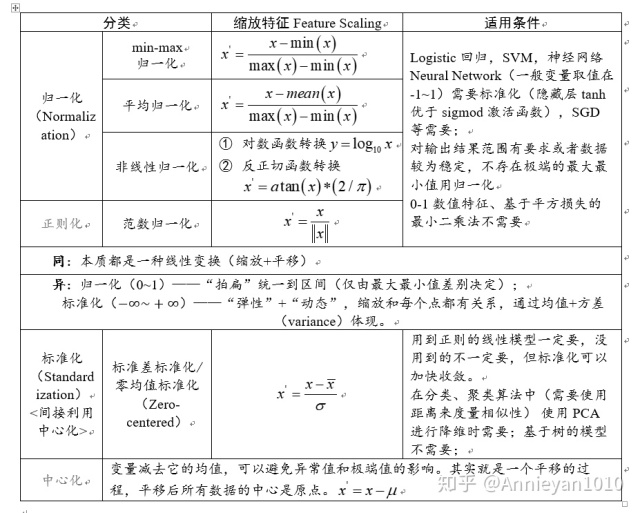
有四种访问修饰符规定了定义的属性和方法能访问的区域

1. private关键字
   用private关键字修饰的属性和方法只能在该类的大括号内访问，出了这个类就不能被访问了。当一个子类继承一个父类的属性和方法时，若父类的属性或方法被private修饰，那么子类就不可以继承该属性或方法。
2. default关键字（包访问权限）
   default关键字修饰的属性或方法只能在同一个包中的所有类访问，且必须是同级的包，在一个包中的子包也不可以访问。但我们在定义属性和方法时不需要将default关键字写出来，没有关键字修饰的属性或方法就是包访问权限。
3. protected关键字（继承访问权限）
   被protected关键字修饰的属性或方法只能在同一个包中的所有类和不同包中的子类访问，出了一个包但不是该类的子类的话就不可以访问。
4. public关键字
   被public关键字修饰的属性或方法可以在任意位置被访问，没有使用的权限。

所以这四种访问修饰符使用的范围从小到大依次是
private < default < protected < public