Java实现矩阵的加、减、乘、数乘、转置、幂运算

首先需要一个矩阵对应的类 Matrix.
命名为Matrix

import java.util.Arrays;
/*** @author yiran* @creat 2021-11-26-13:58*/
public class Matrix{// 矩阵private double[][] matrix;// m x n private int m;private int n;public double[][] getMatrix() {return matrix;}public Matrix() {}public Matrix(double[][] matrix) {this.matrix = matrix;this.m=matrix.length;this.n=matrix[0].length;}public Matrix(int m, int n) {this.matrix=new double[m][n];this.m=m;this.n=n;}public void setMatrix(double[][] matrix) {this.matrix = matrix;this.m=matrix.length;this.n=matrix[0].length;}public int getM() {return m;}public void setM(int m) {this.m = m;}public int getN() {return n;}public void setN(int n) {this.n = n;}//  打印矩阵public void print(){System.out.println("------------------结果-------------------");for (int i=0;i<m;i++){for (int j=0;j<n;j++){System.out.print(matrix[i][j]+"   ");}System.out.println();}System.out.println("----------------------------------------");}@Overridepublic String toString() {return "Matrix{" +"matrix=" + Arrays.toString(matrix) +'}';}
}

之后就是操作矩阵进行运算的工具类 Matrixs.
注意要先复制上面的Matrix矩阵类,再复制下面的工具类,然后将导入的包导一下即可

/*** 方阵的辅助类* @author yiran* @creat 2021-11-26-14:08*/
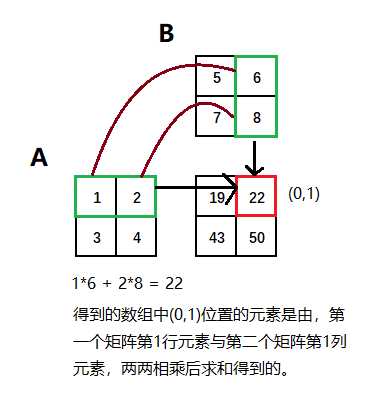
public class Matrixs{/*** 实现矩阵的加法* @param p1 矩阵1* @param p2 矩阵2* @return 如果矩阵不可加,返回null*/public static Matrix plus(Matrix p1,Matrix p2){if (p1!=null&&p2!=null){if (p1.getM()== p2.getM()&&p1.getN()== p2.getN()){double[][] m1 = p1.getMatrix();double[][] m2 = p2.getMatrix();// 矩阵可加的条件满足// 创建矩阵Matrix m=new Matrix();double [][] m_data=new double[p1.getM()][p1.getN()];for (int i=0;i< p1.getM();i++){// a[0]for (int j=0;j< p1.getN();j++){m_data[i][j]=m1[i][j]+m2[i][j];}}m.setMatrix(m_data);return m;}else{// 矩阵不可加System.out.println("矩阵不可加!");return null;}}return null;}/*** 矩阵减法* @param p1* @param p2* @return 如果矩阵不可加,返回null*/public static Matrix minus(Matrix p1,Matrix p2){if (p1!=null&&p2!=null){if (p1.getM()== p2.getM()&&p1.getN()== p2.getN()){double[][] m1 = p1.getMatrix();double[][] m2 = p2.getMatrix();// 矩阵可加的条件满足// 创建矩阵Matrix m=new Matrix();double [][] m_data=new double[p1.getM()][p1.getN()];for (int i=0;i< p1.getM();i++){// a[0]for (int j=0;j< p1.getN();j++){m_data[i][j]=m1[i][j]-m2[i][j];}}m.setMatrix(m_data);return m;}else{// 矩阵不可加System.out.println("矩阵不可减!");return null;}}return null;}/*** 实现矩阵的乘法* @param p1 矩阵1* @param p2 矩阵2* @return 如果矩阵不可乘,返回null*/public static Matrix mutil(Matrix p1,Matrix p2){if (p1!=null&&p2!=null){// 判断矩阵是否可以相乘if (p1.getN()==p2.getM()){double[][] m1 = p1.getMatrix();double[][] m2 = p2.getMatrix();// 矩阵可乘double [][] m =new double[p1.getM()][p2.getN()];for (int i=0;i<p1.getM();i++){for (int j=0;j<p2.getN();j++){double a=0;// 核心for (int k=0;k<p1.getN();k++){a+=m1[i][k]*m2[k][j];}m[i][j]=a;}}return new Matrix(m);}else{// 矩阵不可乘System.out.println("矩阵不可乘!");return null;}}return null;}// 矩阵转置public static Matrix reverse(Matrix m){if(m!=null){Matrix new_m=new Matrix();double[][] m_data = m.getMatrix();double[][] new_m_data=new double[m.getN()][m.getM()];for (int i=0;i<m.getN();i++){for (int  j=0;j<m.getM();j++){new_m_data[i][j]=m_data[j][i];}}m.setMatrix(new_m_data);return m;}return null;}/*** 矩阵的幂运算* @param m 矩阵对象* @param count  运算次数* @return  如果矩阵不是方阵,则矩阵无法进行*/public static Matrix  mutils(Matrix m,int count){if (m!=null&&m.getM()==m.getN()){double[][] matrix = m.getMatrix();Matrix result = new Matrix(matrix);// [A]^countfor (int i=0;i<count-1;i++){result = Matrixs.mutil(result,new Matrix(matrix));}return result;}return  null;}// 矩阵数乘public static Matrix numtil(Matrix m,double num){if(m!=null){Matrix new_m=new Matrix();double[][] m_data = m.getMatrix();double[][] new_m_data=new double[m.getM()][m.getN()];for (int i=0;i<m.getM();i++){for (int  j=0;j<m.getN();j++){new_m_data[i][j] = num * m_data[i][j];}}new_m.setMatrix(new_m_data);return new_m;}return null;}}

然后通过调用工具类中的方法就可以进行矩阵的运算了.
.如果只是需要操作进行运算,复制上面的代码就够了.

---

如果只是要通过输入的数值只进行矩阵乘法的计算,那么本人另外写了一个类,直接用下面的代码,上面的就不需要了,一个类就可以搞定 类名为 MatrixFormulas运行MatrixFormulas 类中的main方法即可开始.

import java.util.Arrays;
import java.util.Scanner;/*** @author yiran* @creat 2021-11-27-11:03*/
public class MatrixFormulas {// 第一个矩阵的m与nprivate static int m1;private static int n1;// 第二个矩阵的m与nprivate static int m2;private static int n2;// 输入的句矩阵数private static boolean count;// 输入流private static Scanner scan;// 矩阵1private static Matrix mat1;// 矩阵2private static Matrix mat2;// 处理输入错误private static boolean flag;// 读取矩阵private static void readFirst(){// 处理输入错误if (flag){scan.nextLine();}while(true){String c=count?"一":"二";System.out.print("请输入第"+c+"个矩阵A的行与列(m n):");String s = scan.nextLine();String[] s1 = s.trim().split(" ");if (s1!=null&&s1.length!=2){System.out.println("输入错误!请重新输入");continue;}//  解析if (count){m1=Integer.parseInt(s1[0]);n1=Integer.parseInt(s1[1]);}else{m2=Integer.parseInt(s1[0]);n2=Integer.parseInt(s1[1]);}double [][] d1=new double[Integer.parseInt(s1[0])][Integer.parseInt(s1[1])];System.out.println("请输入矩阵的数据:");System.out.println("如果遇到要输入多一行的情况,请直接回车");for (int i=0;i<Integer.parseInt(s1[0]);i++){// 一行一行地赋值System.out.print("第"+(i+1)+"行: ");String s2 = scan.nextLine();String[] s3 = s2.trim().split(" ");if (s3.length!=Integer.parseInt(s1[1])){// 再次输入i--;System.out.println("输入格式错误,请重新输入!");continue;}for (int j=0;j<Integer.parseInt(s1[1]);j++){d1[i][j]=Double.parseDouble(s3[j]);}}// 赋值if(count){mat1=new Matrix(d1);break;}else{mat2=new Matrix(d1);break;}}}public static void main(String[] args) {flag=false;scan=new Scanner(System.in);while (true){System.out.println("-----------------矩阵乘法----------------");// 第一次输入count=true;readFirst();// 第二次输入count=false;readFirst();// 计算结果Matrix mutil = Matrixs.mutil(mat1, mat2);mutil.print();System.out.println("----------------------------------------");System.out.print("输入0可以继续:");int i = scan.nextInt();if (i!=0){break;}// 处理输入错误flag=true;}}}/*** 方阵的矩阵类* @author yiran* @creat 2021-11-26-14:08*/
class Matrixs{/*** 实现矩阵的乘法* @param p1 矩阵1* @param p2 矩阵2* @return 如果矩阵不可乘,返回null*/public static Matrix mutil(Matrix p1,Matrix p2){if (p1!=null&&p2!=null){// 判断矩阵是否可以相乘if (p1.getN()==p2.getM()){double[][] m1 = p1.getMatrix();double[][] m2 = p2.getMatrix();// 矩阵可乘double [][] m =new double[p1.getM()][p2.getN()];for (int i=0;i<p1.getM();i++){for (int j=0;j<p2.getN();j++){double a=0;// 核心for (int k=0;k<p1.getN();k++){a+=m1[i][k]*m2[k][j];}m[i][j]=a;}}return new Matrix(m);}else{// 矩阵不可乘System.out.println("矩阵不可乘!");return null;}}return null;}}/*** @author yiran* @creat 2021-11-26-13:58*/
class Matrix{// 矩阵private double[][] matrix;private int m;private int n;public double[][] getMatrix() {return matrix;}public Matrix() {}public Matrix(double[][] matrix) {this.matrix = matrix;this.m=matrix.length;this.n=matrix[0].length;}public Matrix(int m, int n) {this.matrix=new double[m][n];this.m=m;this.n=n;}public void setMatrix(double[][] matrix) {this.matrix = matrix;this.m=matrix.length;this.n=matrix[0].length;}public int getM() {return m;}public void setM(int m) {this.m = m;}public int getN() {return n;}public void setN(int n) {this.n = n;}public void print(){System.out.println("------------------结果-------------------");for (int i=0;i<m;i++){for (int j=0;j<n;j++){System.out.print(matrix[i][j]+"   ");}System.out.println();}System.out.println("----------------------------------------");}@Overridepublic String toString() {return "Matrix{" +"matrix=" + Arrays.toString(matrix) +'}';}
}

编译运行:
注意:如果是在命令行中进行编译的,进入到类对应目录后,执行javac时,
需要指定编码为utf-8,否则会报乱码错误(“因为注释还有输出语句是中文的”),要求编码方式也设置为utf-8,见下面的格式,编译后会多三个class文件

javac -encoding utf-8 MatrixFormulas.java

之后使用java 命令运行即可(不要加上.class的后缀),否则会报无法加载主类的错误

java MatrixFormulas

测试样例