07-行向量列向量_向量的运算加法，数乘，减法，转置

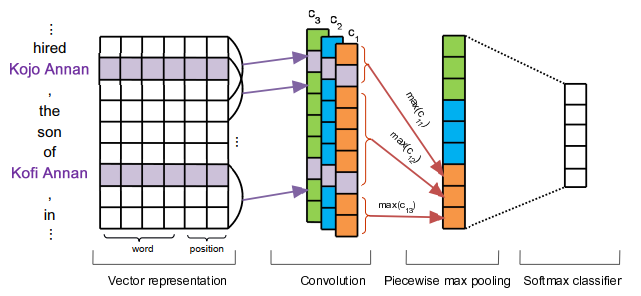
行向量和列向量

其实它们非常简单，所谓的行向量就是我们的向量表示，一组数这组数码成一行，那么所谓的列向量呢？就是这组数码成一列而已，那么对于行向量还是列向量，在我们的学习中是并没有区别的，我们这篇呢，只讲向量，那么对于向量呢，就是一组有序的数字，我们怎么码它并不重要。但是当我们到矩阵的时候，怎么码这个向量的这一组数据就变得有关系了。

行向量是按行把向量排开（横着来写），列向量是按列把向量排开（竖着来写）
在这里插入图片描述

在数学中我们更多的把数据写成列向量，在编程语言中更多的把数据存成行向量! 在这里插入图片描述

如果想在编程语言中把行向量转化成列向量的形式可以用reshape方法重新定义数组形状，不过变化形状后的数组，它的维度也会改变;T属性不是没用，它虽然形式上没变，但a.T是一个列向量，它会在后面进行矩阵操作的时候，能够明显的看到转置后的区别。
在这里插入图片描述

reshape 方法中的 -1 表示自动计算该维度的大小。当你在调用 reshape 方法时，如果将某一个维度设置为 -1，NumPy 会根据数组的总元素个数和其他维度的大小自动计算该维度的大小，以保持数组的原始元素总数不变。

向量的运算加法，数乘，减法，转置

光上面定义向量是没有用的，肯定还要定义向量的一些运算，它有加减乘除一些运算，下面我们一一列举：
在这里插入图片描述

向量 X+Y

等于它们的分量分别相加，显然两个向量的长度得是相等的，减法我们在这里不列举，很容易举一反三

向量相加的和是以AB为边所对应的平行四边形的对角线，相应的这个向量就是a+b。

在这里插入图片描述

向量的加法实际上大家可以理解成我们从原点出发，先走到（5， 2）这个位置。之后再从（5， 2）这个位置出发走（2， 5），相当于是（2， 5）这个向量所对应的这么多的位移。最终，我们到达的这个位置就是向量加法的结果。那么，这个最终的结果，大家可以看到。相当于是从零零这个位置到达了这个位置，我们在这里呢，绘制出了这样的一个三角形的形状。
如果我们在这个三角形的另外一侧相应的也补上和这两个向量平行的这两条边的话，那么大家就可以看到向量加法的最终结果，其实就是以这两个向量为边所对应的这个平行四边形的对角线，那么这就是为什么两个向量相加之后，最终的结果是这样的一个平行四边形的对角线的原因。
那么，具体的从数值的角度讲，这两向量相加结果是什么呢？答案是（7， 7），也就是两个向量相加的结果是将这两个向量中每一个分量分别相加，最终组合成的一个向量。大家也可以验证一下

在这里插入图片描述

那么，这样的一个数值计算的结果和我们在这里直观的看到的这个向量加法的几何意义？他们之间的关系是什么呢？其实也非常好理解。大家可以想象一下。在这里，对于我们(5, 2)这个向量，在我们的坐标轴中，它就可以理解成是先向这个x的正方向移动五个单位，再向y的正方向移动两个单位。之后我们又加上了一个(2, 5)，那么(2, 5)这个向量呢？其实就是向量在(5, 2)这个点的基础上，再向x的正方向移动两个单位，之后再向y的正方向移动五个单位。那么总共我们在x方向就移动了7个单位，而在y这个方向上呢，也是七个单位，这样一来我们就得到了（5, 2）和(2, 5)这两个向量相加，它们的数值结果是(7, 7), 对应的几何儿就直观的表示在坐标轴中，是这两个向量围边所对应的平行四边形的对角线，那么这就是向量的加法。
$\begin{pmatrix}5 \\ 2\end{pmatrix} + \begin{pmatrix} 2\\5\end{pmatrix} = \begin{pmatrix} 7\\ 7\end{pmatrix}$
三维空间也同理
$\begin{pmatrix}1 \\ 2\\3\end{pmatrix} + \begin{pmatrix} 4\\5 \\6\end{pmatrix} = \begin{pmatrix} 5\\ 7\\9\end{pmatrix}$
n维向量也同理
$\begin{pmatrix}v_1 \\v_2 \\\cdots \\v_n\end{pmatrix} + \begin{pmatrix}u_1 \\u_2 \\\cdots \\u_n\end{pmatrix} = \begin{pmatrix}v_1 +u_1\\v_2 + u_2\\\cdots \\v_n + u_n\end{pmatrix}$

数乘(数量乘法) 运算

它是一个数和这个向量的每个分量相乘, 其实就相当于多次的加法操作而已，在坐标系中表示就是一个向量走了多次
$2\times \begin{pmatrix}1 \\ 2\\3\end{pmatrix} = \begin{pmatrix}2 \\ 4\\6\end{pmatrix} = \begin{pmatrix}1 \\ 2\\3\end{pmatrix} + \begin{pmatrix}1 \\ 2\\3\end{pmatrix}$
$k\times(a, b)^T = ?$
n维向量同理：
$k.\begin{pmatrix}v_1 \\v_2 \\\cdots \\v_n\end{pmatrix} = \begin{pmatrix}k.v_1 \\k.v_2 \\\cdots \\k.v_n\end{pmatrix}$
其实就相当于：总共向x移动Ka个单位，总共向y移动kb个单位，最终结果 $(ka, kb)$

在这里大家一定要注意好，对于向量加法和数乘这两种运算，它们的运算对象是不一样的。对于向量的加法，它是定义在两个向量上的一个运算，而对于向量的数乘，它是定义在一个标量和一个向量上的运算

转置

把列向量变成行向量，把行向量变成列向量。
行向量和列向量在现阶段，没有区别
对于通常的教材或者论文来说，一旦提到了一个向量，都是指列向量，换句话说，我们习惯性的更愿意把向量中的这些数字码成一列，而并不是一行。虽然我们在阅读的时候是一行一行的这样阅读的，具体我们为什么更愿意把向量这些数字码成一列？对于这背后的原因，我们也会在后面向大家具体介绍。由于我们的书籍印刷是一行一行的。进行印刷的那么为了表示这个列向量，有的时候就会使用这样的一种符号，（3, 4）这个向量我们先把它写成一行。之后在右上角标一个T 变成 $3, 4)^T$ 这个其实是一个运算符号，表示的是把这个向量进行一下转置的操作。那么，具体什么是转置操作？如下图就是一个转置的过程。

其实它所做的事情就是把这个行向量颠倒90度变成一个列向量，这样呢，我们就可以在一个行的空间中表达一个列向量，因为我们把这些数字码成一列太占空间，太占版面了。只是这个原因而已，那么对于这些约定俗成的符号儿，大家在这里先有一个了解，后面会详细介绍.

🎯实战—实现属于我们自己的向量

我们说过向量其实就是组有序的数字，那么在计算机程序中，数组就是个最直接的来表示一组有序数字的方式，所以我们设计成我们的用户，如果想构造一个向量相应的对象类的话。就只需要在构造函数中传入一个数组就好了，那么python中数组叫做list，对应的这个传进来的参数名，我就管它叫做list这样的一个缩写lst,那么相应的这个lst的内容，我就把它传给我在我们的这个vector中设置一个叫做values这样的一个私有的变量，这个私有的变量。具体的使用一个数组的方式来存储

__repr__魔术方法是供系统来调用的
__str__魔术方法是供用户来调用的，用户使用print方法打印出变量的方式

其实就是对于represent这个函数所返回的字符串儿，应该表示的是我们的这个类的对象对应的构造方法应该写成什么样子的一个字符串儿，而对于。str所返回的结果就是从用户的角度来看，这个对象是什么样子。

文件结构：

├───Linear_Algebra
│   │   main_vector.py
│   │           
│   ├───playLA
│   │   │   Vector.py
│   │   │   __init__.py

Vector.py:

# coding: utf-8class Vector:def __init__(self, lst):self._values = lstdef __getitem__(self, index):"""取向量的第index个元素"""return self._values[index]def __len__(self):"""返回向量的长度（有多少个元素）实际上就相当于向量的维度"""return len(self._values)# 定义显示向量的方法--系统调用def __repr__(self):return 'Vector({})'.format(self._values)# 定义显示向量的方法--用户调用def __str__(self):return "({})".format(", ".join(str(e) for e in self._values))

main_vector.py:

from playLA.Vector import Vectorif __name__ == '__main__':vec = Vector([5, 2])print(vec)print(len(vec))print("vec[0] = {0}, vec[1] = {1}".format(vec[0], vec[1]))