什么是向量

向量是指具有大小和方向的量。它可以形象化地表示为带箭头的线段
箭头所指：代表向量的方向
线段长度：代表向量的大小

向量是线性代数中最基础、最根源的组成部分，向量加法和向量乘法贯穿线性代数始终，起着很重要的作用

基向量

也可以说是单位向量，其他向量都可以由基向量进行缩放、合成得到
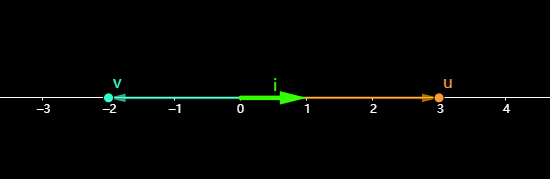
比如在一维坐标系，基向量是$\vec{i}$
$\vec{u}$就可以表示为3$\vec{i}$,$\vec{v}$表示为-2$\vec{i}$

在二维向量中，比如 $\vec{p}$(3,2) =>3*($\vec{i}$,0)+(-2)*(0,$\vec{j}$)

向量数乘

k*(x,y,z) = (kx,ky,kz)
其实就是对向量个轴上的分量进行等比缩放

向量的加法

可以从力学角度看，F1和F2的合力
在X轴上的合力FX = 1 + 3 = 4
在Y轴上的合力FY = 2 + (-1) = 1
最后在将FX和FY进行合成得到F = (4,1)

向量点乘

这里慢慢变得有意思了……
先来一个二维向量

在基向量$\vec{i}$、$\vec{j}$构成的二维坐标系下，向量$\vec{p}$可以表示为：$\vec{p}$ = 3*($\vec{i}$,0) + 2*(0,$\vec{j}$)
但是如果在其他基向量构成的坐标系中，$\vec{p}$应该如何表示？

先来看看$\vec{p}$在$\vec{i}$所在轴上的表示，前面说过，任何向量都可以看做基向量缩放再合成的结果，所以我们只需要变换基向量即可
(0,$\vec{j}$)在水平轴上的表示为(0,0)
($\vec{i}$,0)在水平轴上的表示为($\vec{i}$,0)
在水平轴上$\overrightarrow{p2}$表示为： 3*($\vec{i}$,0) + 2*(0,0) = （3$\vec{i}$,0)，由于这里只有一个轴，后面的分量其实是没意义的，所以可以写成3$\vec{i}$

接下来试着将$\vec{p}$表示在L轴上，$\vec{u}$是在L轴上的单位向量


将($\vec{i}$,0)，(0,$\vec{j}$) 转换到L轴后变成了$\overrightarrow{i2}$、$\overrightarrow{j2}$，那么$\overrightarrow{p2}$ = 3*$\overrightarrow{i2}$ + 2*$\overrightarrow{j2}$

那$\overrightarrow{i2}$、$\overrightarrow{j2}$怎么表示呢？它们跟基向量$\vec{u}$有什么关系？

根据对偶性，可以看出$\vec{i}$在$\vec{u}$上的投影长度和$\vec{u}$在$\vec{i}$上的投影长度相等，那么上面的$\overrightarrow{i2}$ = $u_x$$\vec{u}$，同理$\overrightarrow{j2}$ = $u_y$$\vec{u}$
这里的$\vec{u}$是单位向量，那对于非单位向量呢，比如$\overrightarrow{ku}$ = $k\cdot \vec{u}$，它在$\vec{i}$、$\vec{j}$上的投影是怎样的？

$\overrightarrow{ku}$对$\vec{u}$缩放了$k$倍，对偶性被打破了
$\vec{i}$在$\overrightarrow{ku}$上的投影长度并没有改变，$\vec{i}\cdot \overrightarrow{ku}$ = $k(\vec{i}\cdot \vec{u})$
图中可以看出$\overrightarrow{ku}$在$\vec{i}$上的投影长度被缩放了$k$倍$\overrightarrow{ku}\cdot \vec{i}$ = $k(\vec{u}\cdot \vec{i})$
可见，对于非单位向量，彼此的投影仍然保持一致

所以无论$\vec{u}$是不是单位向量，$\vec{i}$、$\vec{j}$在$\vec{u}$上的投影长度都为$u_x、u_y$
所以：
$\overrightarrow{p2}$ = $p_x\cdot \overrightarrow{i2}$ + $p_y\cdot \overrightarrow{j2}$
= $p_x{u}_x$$\vec{u}$ + $p_y{u}_y$$\vec{u}$
= ($p_x{u}_x+p_y{u}_y$)*$\vec{u}$
= $p_x{u}_x+p_y{u}_y$ （一个轴上的向量可直接用数值表示，数值绝对值表示向量长度，正负表示方向）
到此，我们得到了一个非常重要的结论：
向量$\vec{p}$在向量$\vec{u}$上的表示为 $p_x$$u_x$ + $p_y$$u_y$
根据对偶性，向量$\vec{u}$在向量$\vec{p}$上的表示也为 $p_x$$u_x$ + $p_y$$u_y$
咦，这不是向量点乘公式吗？并且满足交换律！
继续看，是不是觉得这个公式有点眼熟……
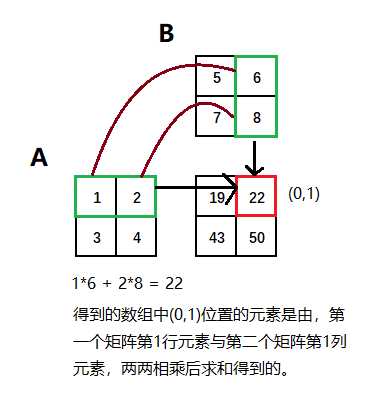
矩阵乘法：
$[\begin{array}{c}a\\ b\end{array}]$$\cdot$$\begin{array}{cc}[c& d]\end{array}$ = $ac+bd$
如果将$\vec{p}$写成列式$[\begin{array}{c}{p}_x\\ p_y\end{array}]$,$\vec{u}$写成行式$\begin{array}{cc}[u_x& u_y]\end{array}$，$\vec{p}\cdot \vec{u}$就可以看做是矩阵乘法
$\vec{p}\cdot \vec{u}$ = $[\begin{array}{c}{p}_x\\ p_y\end{array}]$$\cdot$$\begin{array}{cc}[u_x& u_y]\end{array}$ = $p_x$$u_x$ + $p_y$$u_y$
看到这里，我们是否可以理解为：向量的点乘，其实就是将一个向量变换到另一个向量所在的坐标空间中

如下图：二维空间中的点，经过单位向量$\vec{u}$变换后，在$\vec{u}$所在轴上都能得到与之对应的值，这个过程我们可以看做是二维空间到一维空间的投射

$\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|cos(\phi )$
这个公式又是怎么得到的？

先复习下余弦定理：
$|\vec{a}{|}^2$ = $|\vec{c}{|}^2$ + $|\vec{b}{|}^2$
= $(|\vec{c}|sin(A){)}^2$ + $((|\vec{b}|-|\vec{c}|cos(A){)}^2)$
= $|\vec{c}{|}^2$$sin(A{)}^2$ + $|\vec{b}{|}^2$ + $|\vec{c}{|}^2$$cos(A{)}^2$ - $2|\vec{c}||\vec{b}|cos(A)$
= $|\vec{c}{|}^2$($sin(A{)}^2$ + $cos(A{)}^2$) + $|\vec{b}{|}^2$ - $2|\vec{c}||\vec{b}|cos(A)$
= $|\vec{c}{|}^2$ + $|\vec{b}{|}^2$ - $2|\vec{c}||\vec{b}|cos(A)$

按照上面的推导：
$2|\vec{c}||\vec{b}|cos(A)$ = $|\vec{c}{|}^2$ + $|\vec{b}{|}^2$ - $|\vec{a}{|}^2$
= $B_x^2$ + $B_y^2$ + $C_x^2$ + $C_y^2$ - $(C_x-B_x{)}^2$ - $(C_y-B_y{)}^2$
= $B_x^2$ + $B_y^2$ + $C_x^2$ + $C_y^2$ - $C_x^2$ - $B_x^2$ + $2C_x{B}_x$ - $C_y^2$ - $B_y^2$ + $2C_y{B}_y$
= 2($C_x{B}_x$+$C_y{B}_y$)
得到：$|\vec{c}||\vec{b}|Cos(A)$ = $C_x{B}_x$+$C_y{B}_y$

所以：$\vec{a}\cdot \vec{b}$ = $a_x{b}_x+a_y{b}_y$ = $|\vec{a}||\vec{b}|cos(\phi )$，$\phi$是$\vec{a}\vec{b}$夹角
根据点乘的结果来判断两个向量的方向关系：
大于 0：0 =< $\phi$ < $pi/2$
等于 0： $\phi$ = $pi/2$，两向量垂直
小于 0：$pi/2$ < $\phi$ =< $pi$

从力学角度，是否还可以理解为力F在位移S上做的功?
W = $|\vec{F}||\vec{S}|cos(\phi )$

参考：https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw