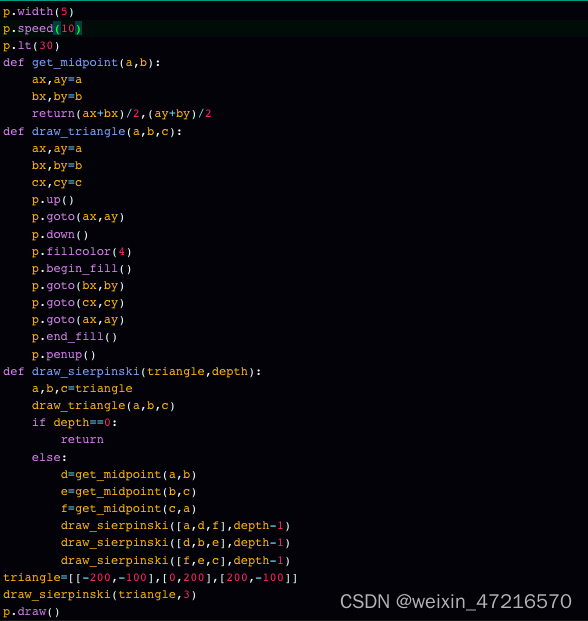
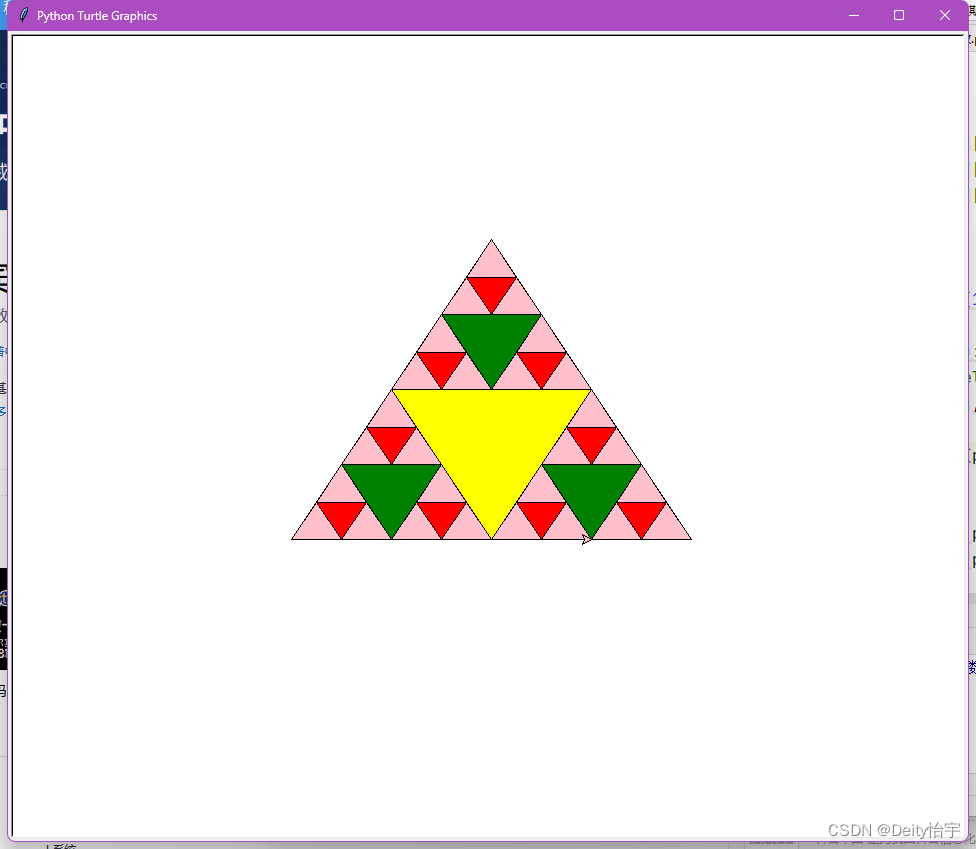
了解谢尔宾斯基地毯

我们先从谢尔宾斯基三角形讲起：
谢尔宾斯基三角形（英语：Sierpinski triangle）是一种分形，由波兰数学家谢尔宾斯基在1915年提出。它是自相似集的例子。
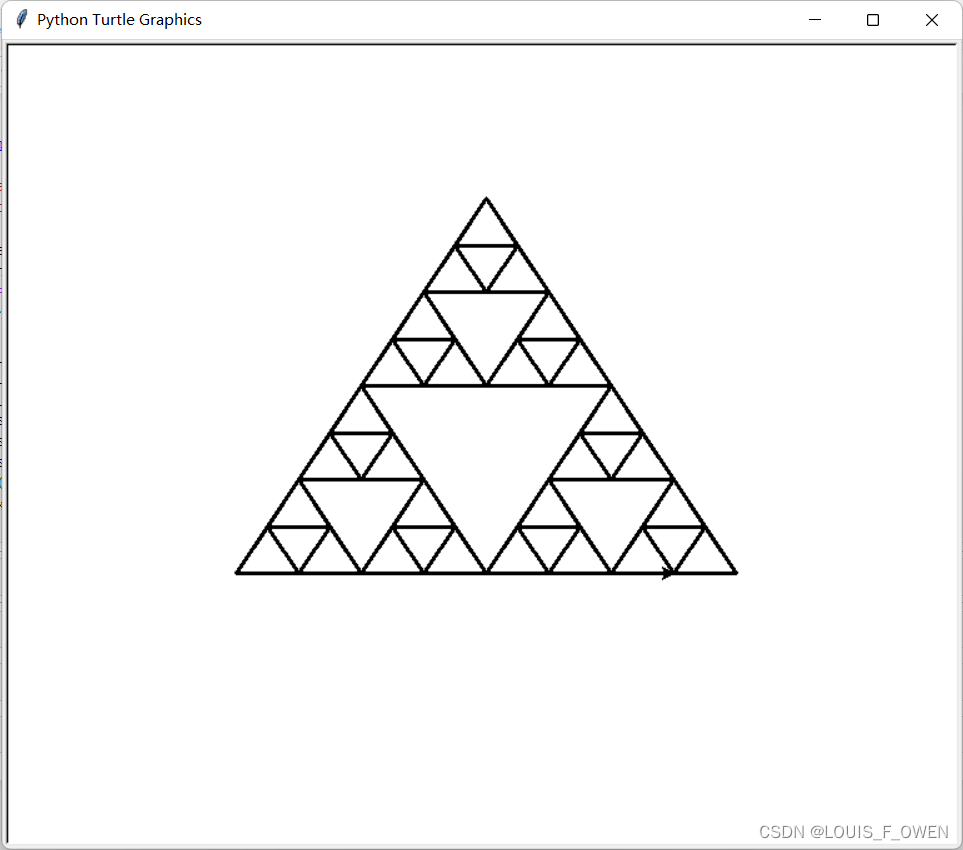
以下是0到3阶的谢尔宾斯基三角形：
在这里插入图片描述

它的构造方法是：
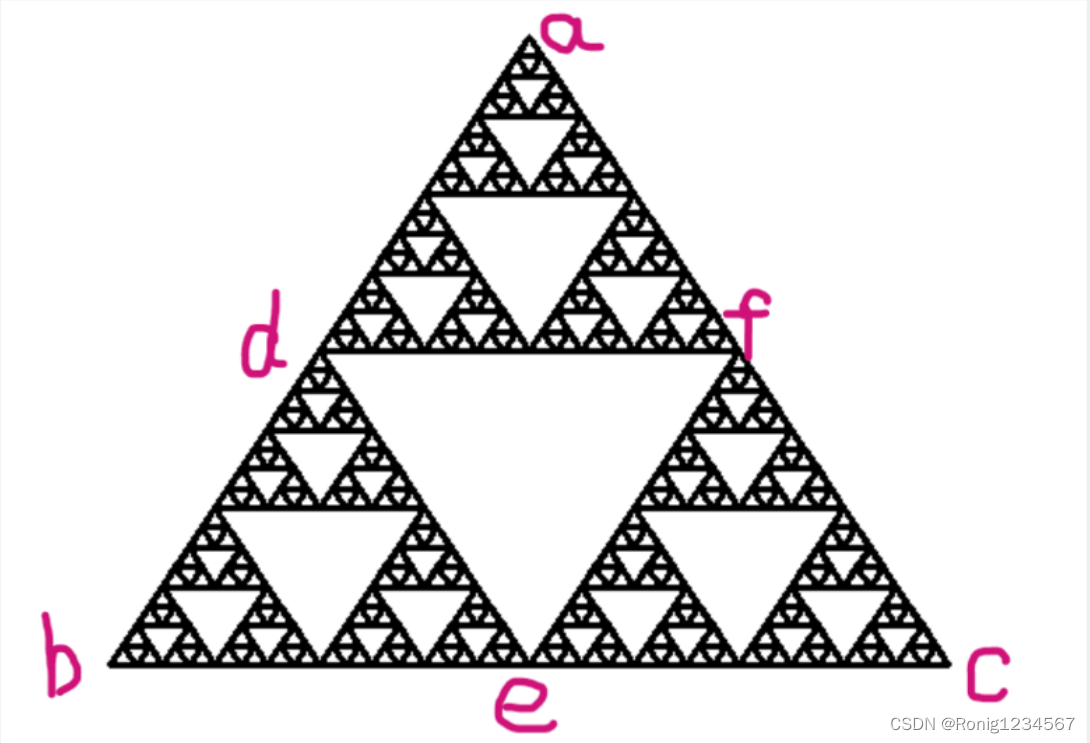
1.取一个实心的等边三角形
2.沿三边中点的连线，将它分成四个小三角形。
3.去掉中间的那一个小三角形。
4.对其余三个小三角形重复（1,2,3）过程。

谢尔宾斯基三角形特点：
容易看出，假设0阶谢尔宾斯基三角形面积为a，周长为b，
那么n阶谢尔宾斯基三角形面积为：a*[(3/4)^n]
周长为：b*[(3/2)^n]
也就是说，当区域无穷大时，我们得到了一个面积为0，但周长却为无穷大的图形。

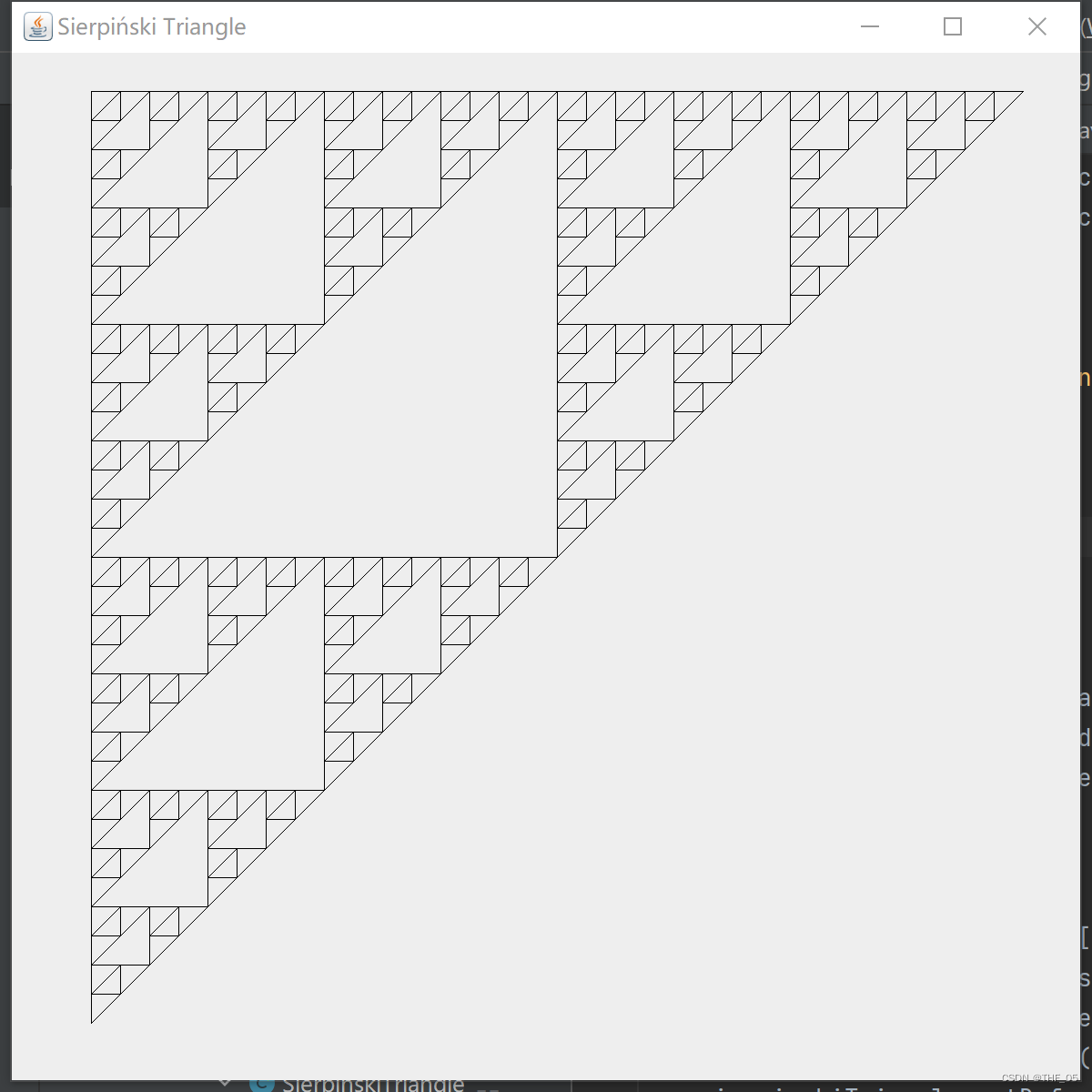
我们再来看谢尔宾斯基地毯，它的基本图形为一个正方形，然后每次挖去中心的一个小正方形，
直接上图：
在这里插入图片描述

海龟作图turtle

python2.6版本中后引入的一个简单的绘图工具，叫做海龟绘图(Turtle Graphics),出现在1966年的Logo计算机语言。
海龟绘图（turtle库）是python的内部模块,使用前导入即可 import turtle
详细用法这里不具体介绍，可以参考下面这篇文章：
python之turtle海龟绘图篇

代码思路：

我们从最简单的情况想起：一阶地毯
我们将大正方形（先假设边长为3a）放在一个直角坐标系中，左下顶点定为（0,0），右上顶点定为
（3a,3a）
那么容易得到：要挖去那一个小三角形，它的左下顶点坐标为（a，a），边长为a
也即：要挖去的区域为{（x，y）|a<=x<=2a,a<=y<=2a}

那么对于n阶的地毯，我们需要考虑的就是不断减小问题规模，使之回到最简单的情况。

使用代码实现时，我们可以考虑：
对于n阶的谢尔宾斯基地毯，我们先将最大的正方形固定在坐标轴上，
然后考虑每一个最小的正方形是否应该挖去，
例如三阶地毯，设最大正方形面积为9*9=81，那么我们只需要考虑每个面积为1的小正方形应该留下或挖去。
下面上代码：

代码

海龟图画谢尔宾斯基地毯
思路：令最小的一个正方形边长为base，则n阶地毯的边长为base*（3**n）
由于turtle画布的长度为600左右，第一象限长度为300左右，我们令base=int（300/（3^n)
判断每一个边长为base的小正方形是否应该挖去

绘制最外围的正方形：

import turtle# 画好最外围的正方形，背景设为蓝色
n = int(input())
t = turtle.Turtle()
base = int(300 / (3 ** n))  # 设置每个小正方形长度base
length = base * (3 ** n)  # 最外围的正方形长度
t.pensize(0.1)
turtle.tracer(False)  # 画图过程太长我们跳过不看
t.pencolor('blue')
t.fillcolor('blue')
t.begin_fill()  # 填充蓝色
for i in range(1, 5):t.forward(length)t.left(90)
t.end_fill()
turtle.done()

运行结果是这样的：
在这里插入图片描述

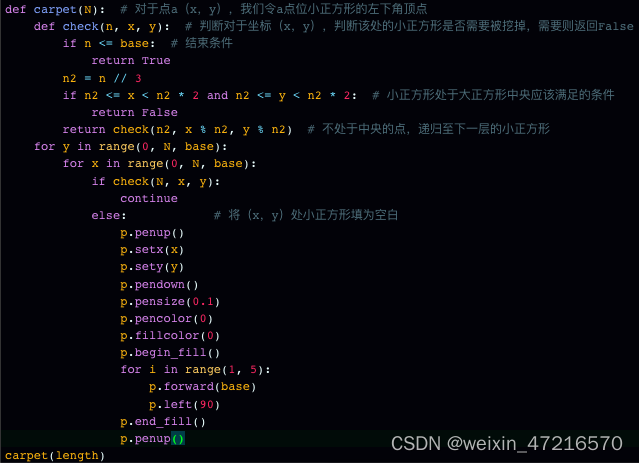
对于每个边长为base的小正方形，是否应该挖去，需要用到递归：

    def check(n, x, y):  # 判断对于坐标（x，y），判断该处的小正方形是否需要被挖掉，需要则返回Falseif n <= base:  # 结束条件return Truen2 = n // 3if n2 <= x < n2 * 2 and n2 <= y < n2 * 2:  # 小正方形处于大正方形中央应该满足的条件return Falsereturn check(n2, x % n2, y % n2)  # 不处于中央的点，递归至下一层的小正方形# 取余的操作可以理解为将零点移至小正方形的左下角顶点

最后我们将所有判断为False的小正方形挖去：

    for y in range(0, N, base):for x in range(0, N, base):if check(N, x, y):continueelse:            # 将（x，y）处小正方形填为空白t.penup()t.setx(x)t.sety(y)t.pendown()t.pensize(0.1)t.pencolor('white')t.fillcolor('white')t.begin_fill()for i in range(1, 5):t.forward(base)t.left(90)t.end_fill()t.penup()

不要忘了输入和输出：

n = int(input())
carpet(length)

最后完整代码是这样的：

import turtle
n = int(input())
# 画好最外围的正方形，背景设为蓝色
t = turtle.Turtle()
base = int(300 / (3 ** n))  # 设置每个小正方形长度base
length = base * (3 ** n)  # 最外围的正方形长度
t.pensize(0.1)
turtle.tracer(False)  # 画图过程太长我们跳过不看
t.pencolor('blue')
t.fillcolor('blue')
t.begin_fill()  # 填充蓝色
for i in range(1, 5):t.forward(length)t.left(90)
t.end_fill()def carpet(N):  # 对于点a（x，y），我们令a点位小正方形的左下角顶点def check(n, x, y):  # 判断对于坐标（x，y），判断该处的小正方形是否需要被挖掉，需要则返回Falseif n <= base:  # 结束条件return Truen2 = n // 3if n2 <= x < n2 * 2 and n2 <= y < n2 * 2:  # 小正方形处于大正方形中央应该满足的条件return Falsereturn check(n2, x % n2, y % n2)  # 不处于中央的点，递归至下一层的小正方形# 取余的操作可以理解为将零点移至小正方形的左下角顶点for y in range(0, N, base):for x in range(0, N, base):if check(N, x, y):continueelse:            # 将（x，y）处小正方形填为空白t.penup()t.setx(x)t.sety(y)t.pendown()t.pensize(0.1)t.pencolor('white')t.fillcolor('white')t.begin_fill()for i in range(1, 5):t.forward(base)t.left(90)t.end_fill()t.penup()carpet(length)
turtle.done()