Python递归绘制谢尔宾斯基三角形

article/2025/8/29 14:34:49

首先，回顾递归的概念：

一个函数不停地调用它本身，我们就认为这个函数使用了递归。

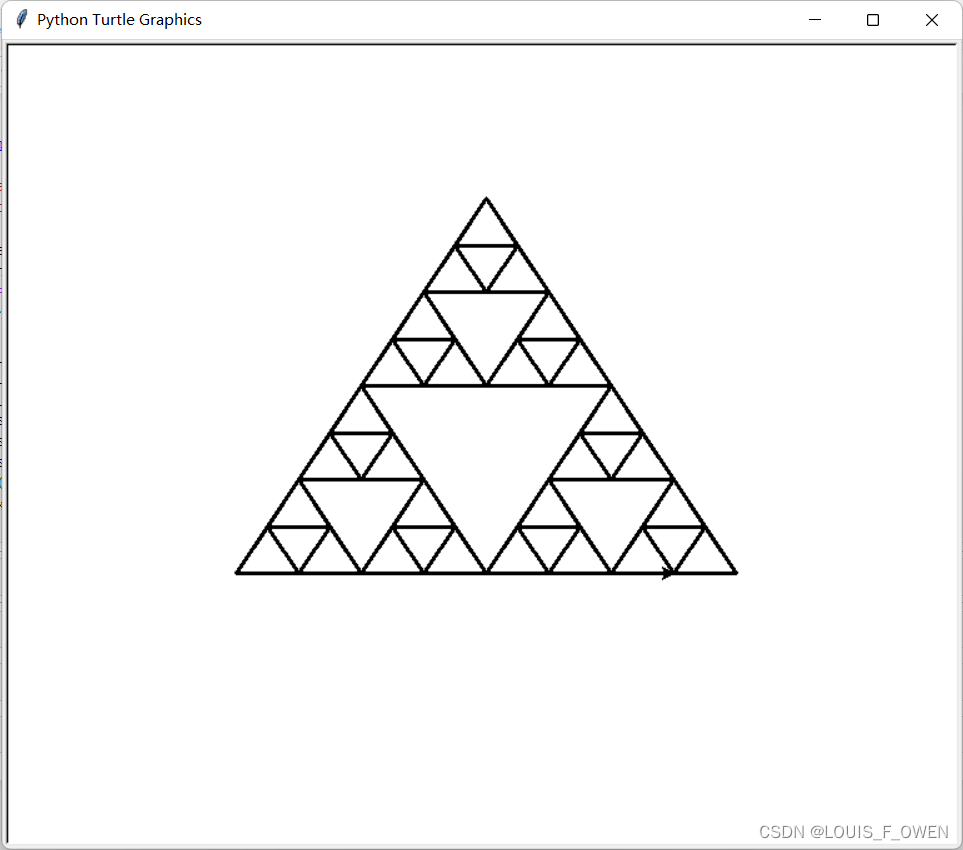
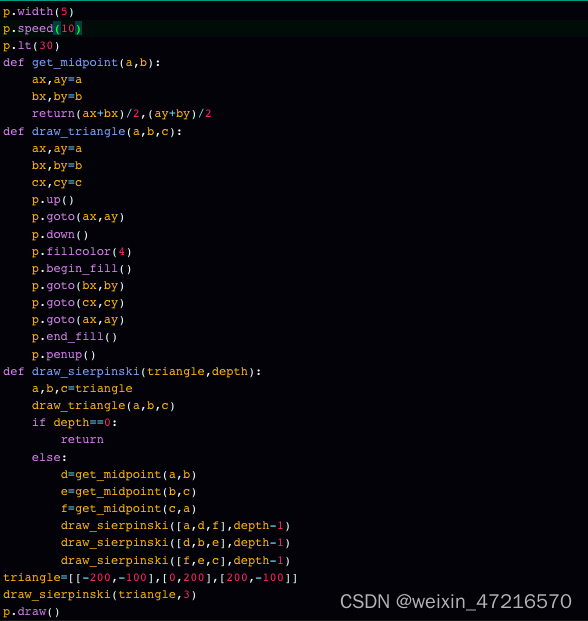
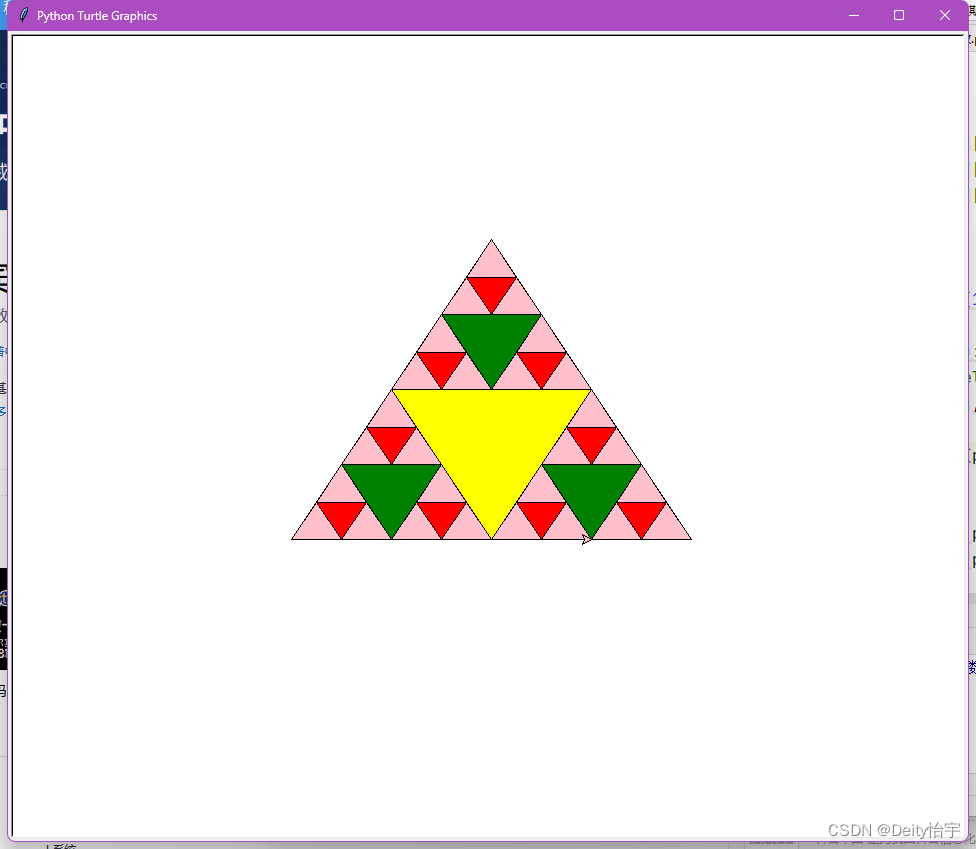
先来看一个谢尔宾斯基三角形的示例：

所以首先，我们需要一个方法，它能帮我们画三角形，在这里画一个三角形，需要引入Turtle模块，画三角形需要三个点的坐标，不做过多的叙述。注;规定左下角顶点为p[0]，上方顶点和右顶点分别为p[1]p[2]

from turtle import *
def drawTriangle(points, color, myTurtle):myTurtle.fillcolor(color)myTurtle.up()myTurtle.goto(points[0])myTurtle.down()myTurtle.begin_fill()myTurtle.goto(points[1])myTurtle.goto(points[2])myTurtle.goto(points[0])myTurtle.end_fill()

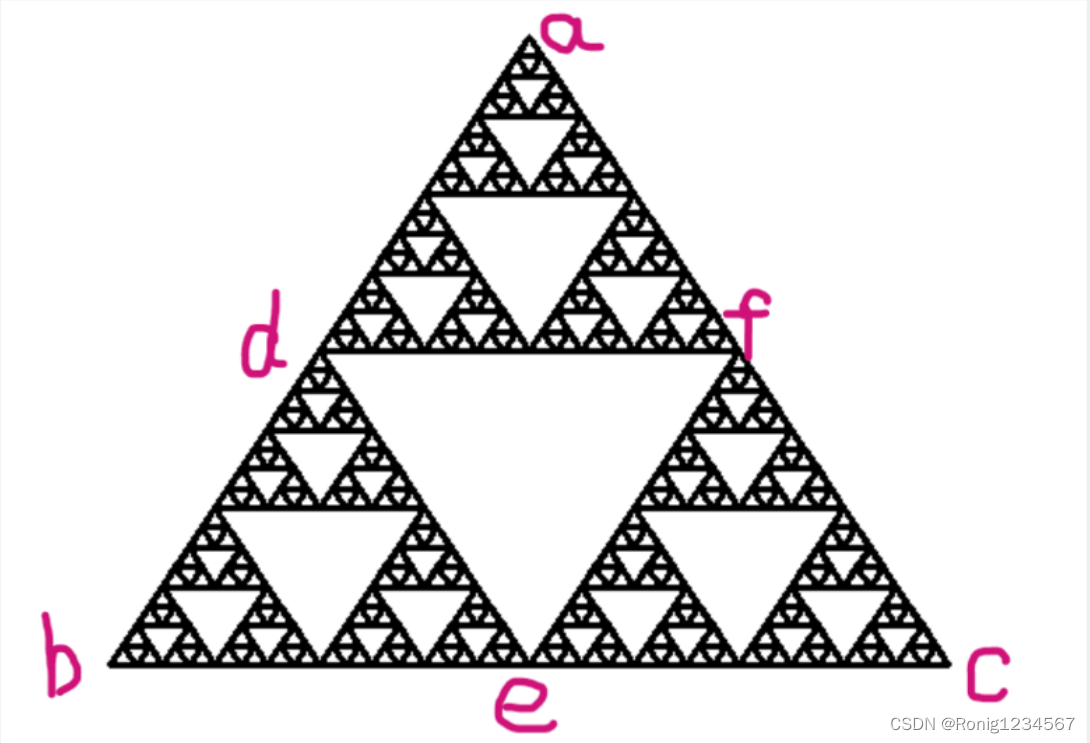
其次，要绘制一个谢尔宾斯基三角形，我们需要从一个大三角形开始，找到每个边的中点，连接起来形成一个三角形（粉色部分）

在把中点连接起来之前，我们要找到中点，找到中点的方法大家高中都学过：

其中p1，p2是坐标，在这里我们用元组的形式表达。

def getMid(p1, p2):return ( (p1[0]+p2[0]) /2, (p1[1] + p2[1]) / 2)

然后我们要开始绘制谢尔宾斯基三角形了，下面考虑它的具体画法：如果我们只简单地分一层，则：

不难注意到，层数为0，就是一个三角形。

画一层，最主要的是找到它的三个中点，然后去绘制一个如上图所示的三角形。

如果层数为2，我们需要将周围的三个三角形再分别进行一次如上的处理，即，找到三个蓝色三角形的中点，然后把这三个中点连上线，忽略中间的三角形。我们不妨把上图看作一个单位，然后进一步地发现，高层数的谢尔宾斯基三角形就是用很多个这个单位构成的：如degree == 2:

所以考虑到它在不断地画相同的三角形，我们在这里当然要使用递归的方法来进行处理。

首先，我们要先画外轮廓的大三角形，代码如下：

def sierpinski(points, degree, myTurtle):colormap = ['blue', 'red', 'green', 'white', 'yellow','violet', 'orange']drawTriangle(points, colormap[degree], myTurtle)

解释一下，colormap是颜色的一个列表，不同的层次用不同的颜色，points接受一个由元组构成的列表，是整个外轮廓大三角形的坐标，然后调用上面的绘制三角形的函数进行绘制外轮廓。

前面提到，如果层数为0，就是一个三角形，此时我们当然没有进行绘制的必要，因此我们需要一个判断语句，再进入到递归的部分：

    if degree>0:

接下来进入到了绘制谢尔宾斯基三角形的环节，我们可以先让Python绘制左下角的三角形，像分形树先走右子树一样，我们先去画左下角的三角形直到degree==0,则对左下角三角的递归完成，绘制左下角的三角形，需要的是大三角形左顶点的坐标和两个中点的坐标，这里可以使用getMid()完成

        sierpinski([points[0],getMid(points[0], points[1]),getMid(points[0], points[2])],degree - 1, myTurtle)

像分形树一样，我们已经绘制出了左下角的三角

然后去绘制p[1]处的三角，我们需要其和p[0]p[2]的中点

        sierpinski([points[1],getMid(points[0], points[1]),getMid(points[1], points[2])],degree - 1, myTurtle)

最后：

         sierpinski([points[2],getMid(points[2], points[1]),getMid(points[0], points[2])],degree - 1, myTurtle)

绘制完成：

from turtle import *def drawTriangle(points, color, myTurtle):myTurtle.fillcolor(color)myTurtle.up()myTurtle.goto(points[0])myTurtle.down()myTurtle.begin_fill()myTurtle.goto(points[1])myTurtle.goto(points[2])myTurtle.goto(points[0])myTurtle.end_fill()def getMid(p1, p2):return ( (p1[0]+p2[0]) /2, (p1[1] + p2[1]) / 2)def sierpinski(points, degree, myTurtle):colormap = ['blue', 'red', 'green', 'white', 'yellow','violet', 'orange']drawTriangle(points, colormap[degree], myTurtle)if degree > 0:sierpinski([points[0],getMid(points[0], points[1]),getMid(points[0], points[2])],degree - 1, myTurtle)sierpinski([points[1],getMid(points[0], points[1]),getMid(points[1], points[2])],degree - 1, myTurtle)sierpinski([points[2],getMid(points[2], points[1]),getMid(points[0], points[2])],degree - 1, myTurtle)myTurtle = Turtle()
myWin = myTurtle.getscreen()
myTurtle.speed(1)
myPoints = [(-200, -100), (0, 200), (200, -100)]
sierpinski(myPoints, 3, myTurtle)
myWin.exitonclick()

整体代码如上面所示，可以考虑把递归中只留下一行代码，看看小乌龟的行动轨迹，比如为什么单独运行第一个递归，代码就一直在画左下角的三角形，而剩下的两个不行呢？（考虑绘制三角形函数的定义）