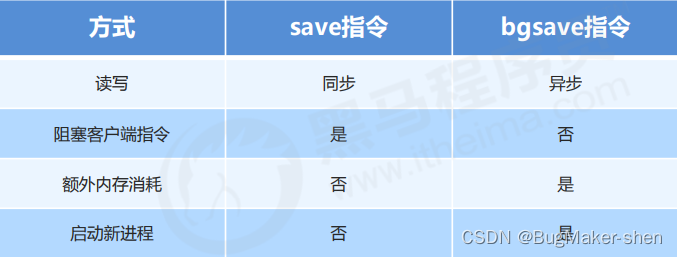
本来觉得谢尔宾斯基三角形挺难的。分析以后，其实还是挺简单的。

挺好理解，供大家一起学习

"""功能：绘制谢尔宾斯基三角形环境：python3.7日期：2019/1/14 21:49作者：指尖魔法师版本：1.0
"""
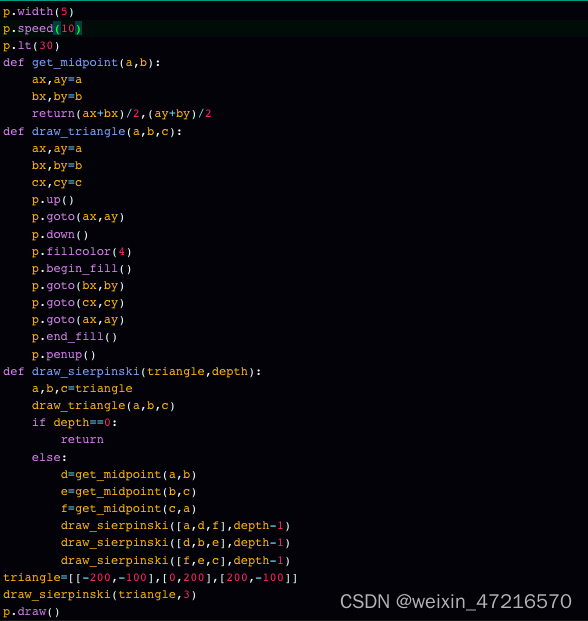
import turtle as tdef sanjiaoxing(san):"""传入三个点坐标，绘制三角形"""t.penup()t.goto(san[0])t.pendown()t.goto(san[1])t.goto(san[2])t.goto(san[0])def get_mid(a, b):"""计算返回2个点的中间点坐标"""x = (a[0] + b[0]) / 2y = (a[1] + b[1]) / 2return [x, y]def draw_san(size, i):"""绘制谢尔宾斯基三角形函数:param size: 三个点坐标列表:param i: 递归次数"""# 绘制三角形sanjiaoxing(size)if i > 0:# 绘制左边小三角形size2 = [size[0], get_mid(size[0], size[1]), get_mid(size[0], size[2])]draw_san(size2, i - 1)# 绘制上边的小三角形size3 = [get_mid(size[0], size[2]), get_mid(size[1], size[2]), size[2]]draw_san(size3, i - 1)# 绘制右边的小三角形size4 = [get_mid(size[0], size[1]), size[1], get_mid(size[1], size[2])]draw_san(size4, i - 1)def main():"""主函数"""# 打印图形标题t.penup()t.left(90)t.forward(350)t.pendown()t.write("谢尔宾斯基三角形", False, align="center", font=("宋体", 20, "normal"))t.speed(5)# 初始三角形坐标points = [[-200, 0], [200, 0], [0, 300]]# 递归5次count = 5# 调用绘制谢尔宾斯基三角形函数draw_san(points, count)t.exitonclick()if __name__ == '__main__':main()

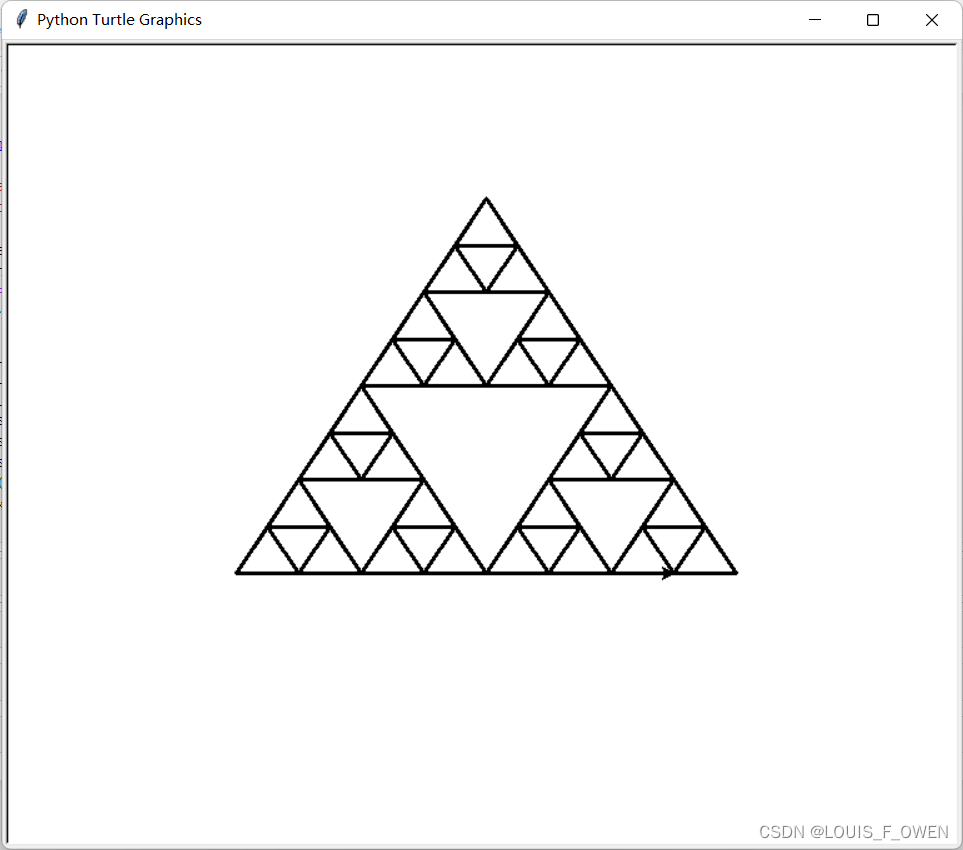
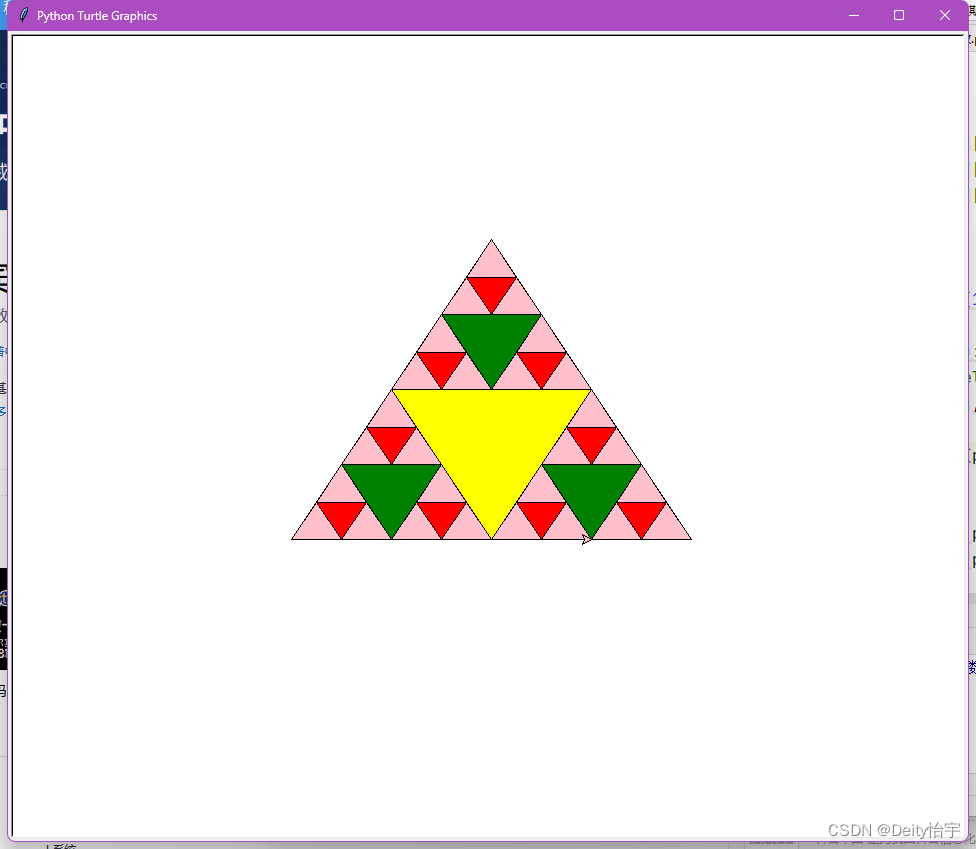
运行结果：