大家好,我叫王若冲。因为我妈叫我冲姐,所以你们也可以这么叫我。今天是我的第一篇文章,就给大家讲谢尔宾斯基三角的代码吧。如果你既想要试一试,又懒得自己写代码,那么原代码就在下面。*注意,这次我用的软件叫做IDLE(Python 3.7 64-bit) ,建议大家用原软件去试。
定一个规矩:如果你只是随便看看,那么还希望你帮我找一找缺点,在今后我会加油填上的!
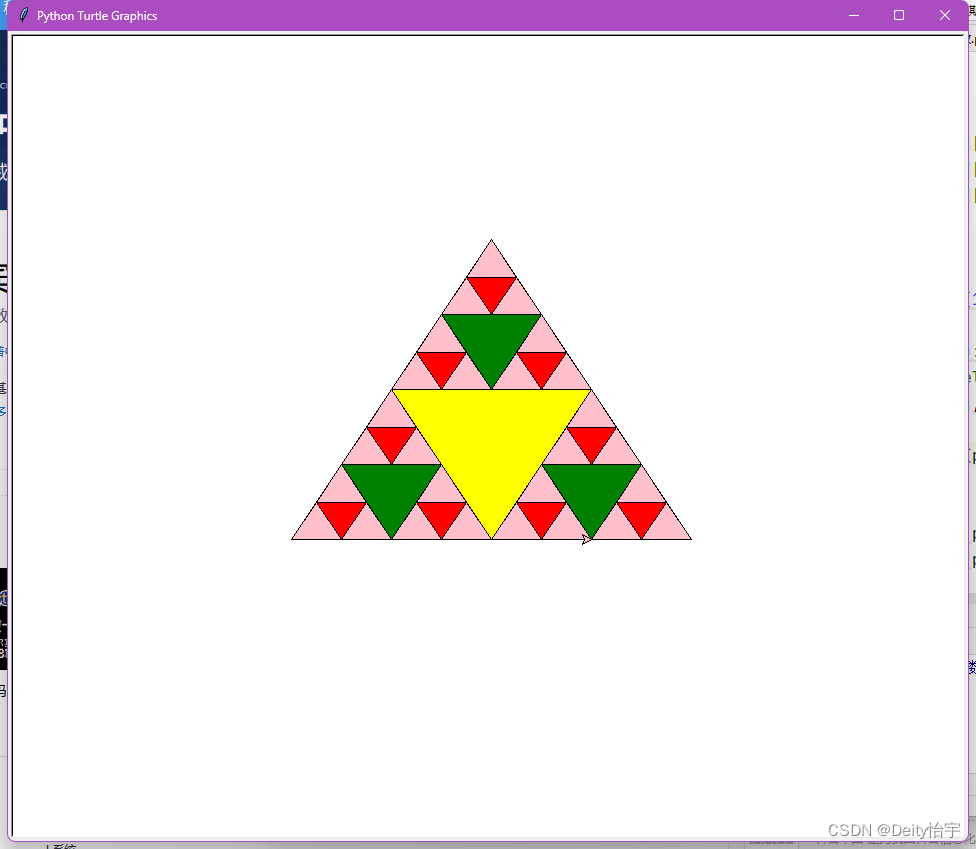
首先,谢尔宾斯基三角是什么?给大家看一张图,你马上就会知道。

没错,直白地说就是分三角形。但是,再仔细看,你会发现小三角形是如何分割的。我们往下看......
假设这个大三角形是abc,那么a与b有一个中点,我们就设它为d。同样,将b与c,c与a的中点取出,分别设为e和f。那么,把这三个中点连接,就会把大三角形abc平均分割成4个同样的较小的三角形,分别为adc、deb、fec和def。把中间的三角形def放在一旁,用同样的方法分割剩下的三个三角形,以此类推,直到你想要停歇为止。
懂得了它的原理,代码就特别简单啦。请看:
import turtle as p
p.width(3)
p.speed(10)
p.setheading(120)
p.hideturtle()
def get_midpoint(a,b):
ax,ay=a
bx,by=b
return(ax+bx)/2,(ay+by)/2
def draw_triangle(a,b,c):
ax,ay=a
bx,by=b
cx,cy=c
p.penup()
p.goto(ax,ay)
p.pendown()
p.goto(bx,by)
p.goto(cx,cy)
p.goto(ax,ay)
def draw_siepinski(triangle,depth):
a,b,c=triangle
draw_triangle(a,b,c)
if depth==0:
return;
else:
d=get_midpoint(a,b)
e=get_midpoint(b,c)
f=get_midpoint(c,a)
draw_siepinski([a,d,f],depth-1)
draw_siepinski([d,b,e],depth-1)
draw_siepinski([f,e,c],depth-1)
triangle=[[-200,-100],[0,200],[200,-100]]
draw_siepinski(triangle,5)
p.done()
第一部分:提前准备
Python可以说它是一个老板,它自己到没有什么本事,但有本事的亲戚特别多。这个亲戚就是Python从外面调用到自己这儿的一个包,你想什么时候用,你就把它请出来,就可以用了。此处,import就是引入的意思,明摆着就是说把turtle这个包调用过来。为了简便,就把它写成p。其它代码就是小乌龟(turtle)的一些设置。
第二部分:取中点函数
在二维图形中,横轴为x,竖轴为y。这里就是定义一个函数来确定ab的中点的确切位置。
第三部分:画大三角形函数
没什么特别,主要是画了一个大三角形(我先前说的abc),用函数表达是为了更迅速、精确地找到位置。
第四部分(***重点!***):往里分割三角形函数
这里就是重点啦!还记得我之前说谢尔宾斯基三角的分割规律吗?这个函数实现了它。我们一步一步理解。
1.参数。此函数中有两个参数,一个是在定义这个函数时肚子里的triangle,就是abc大三角形。另一个叫depths,理解上是深度的意思,在这里就指分割三角形的阶数,一共要分几层。
2.if...else...结构。Python中有3大结构,分别为循环结构、顺序结构、选择结构。if...else...就是选择结构,简单说就是给你多个选择,你选了哪个你就做哪个,不然你就做哪个。把代码解释一遍,就是如果阶数为0,那么就别做了,要不然你就画相应阶数的三角形。
3.递归。在draw_siepinski()函数中,你会发现里面出现了一个自己!这就是递归,自己调用自己。那么你一定会问,如果自己一直调用自己,会不会没完没了了呢?那就不对了,因为每一个递归都有一个终止条件,让它到一定的条件后适可而止。这里,if中的条件(depths=0)则为终止条件,让它阶数到0以后就别画了。
4.三角形+取中点。之前我不是把那个大三角形设置为abc吗,接着取三条边的中点吗?其实你每分完一次,那个准备被分的三角形都可以称之为abc,那些三角形的中点都可以叫d,e,f。并且它每分完一次,它的阶数就减一,一直延续到depths等于0为止。
第五部分:运用函数
将函数运用起来,就可以画出来了哟!
分析完了代码,是不是学到了很多知识?那么就赶紧动一动手,做起来吧!