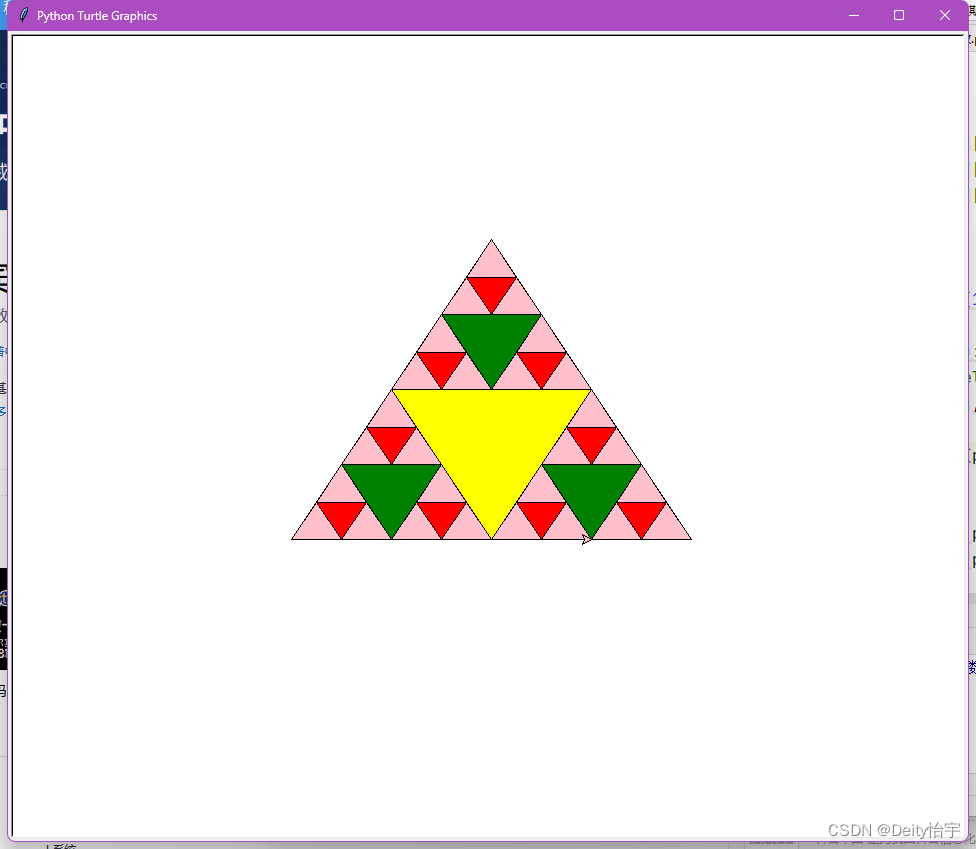
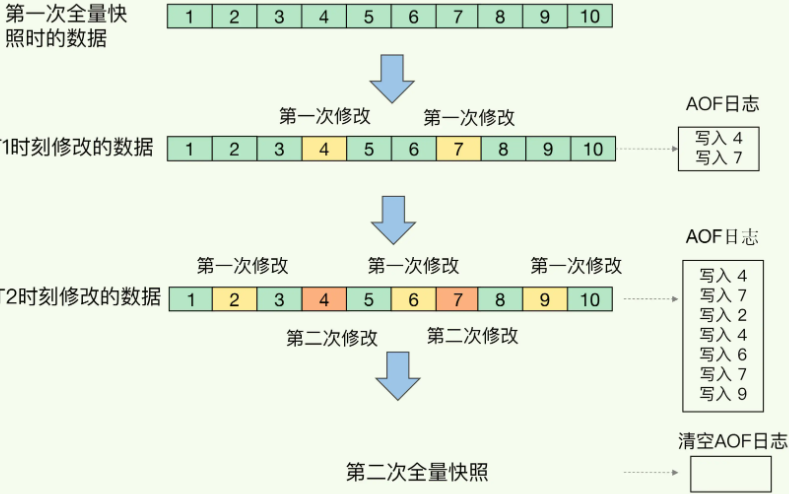
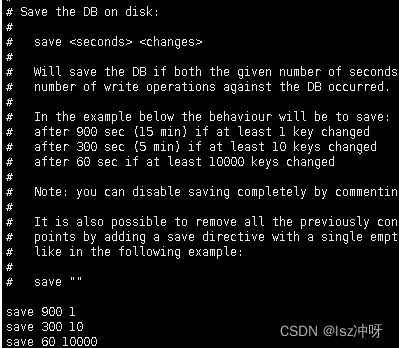
谢尔宾斯基三角形（英语：Sierpinski triangle）是一种分形，由波兰数学家谢尔宾斯基在1915年提出。它是自相似集的例子。它的豪斯多夫维

1.取一个实心的三角形。（多数使用等边三角形）

2.沿三边中点的连线，将它分成四个小三角形。

3.去掉中间的那一个小三角形。

4.对其余三个小三角形重复1。

取一个正方形或其他形状开始，用类似的方法构作，形状也会和谢尔宾斯基三角形相近。

是log(3)/log(2) ≈ 1.585。

假设这个大三角形是abc，那么a与b有一个中点，我们就设它为d。同样，将b与c，c与a的中点取出，分别设为e和f。那么，把这三个中点连接，就会把大三角形abc平均分割成4个同样的较小的三角形，分别为adc、deb、fec和def。把中间的三角形def放在一旁，用同样的方法分割剩下的三个三角形，以此类推，直到你想要停歇为止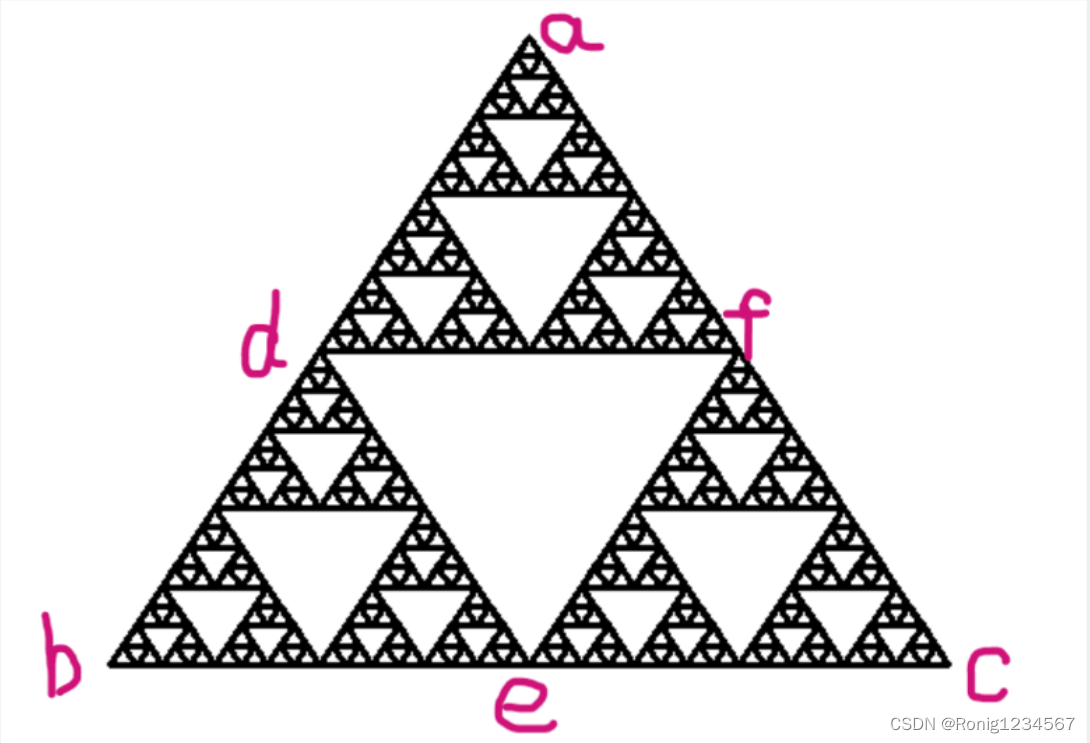

下面是代码

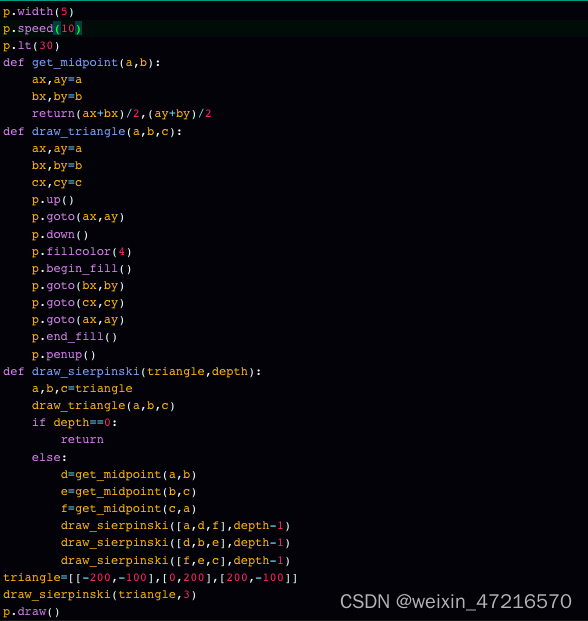
p.width(3)
p.speed(10)
p.lt(30)
def get_midpoint(a, b):ax, ay = abx, by = breturn (ax + bx) / 2, (ay + by) / 2
def draw_triangle(a, b, c):     # [-200, -100], [0, 200], [200, -100]ax, ay = a   #[-200, -100]bx, by = b   #[0, 200]cx, cy = c   #[200, -100]p.penup()p.goto(ax, ay)p.pendown()p.goto(bx, by)p.goto(cx, cy)p.goto(ax, ay)p.penup()
def draw_sierpinski(triangle, depth):""":param triangle: 指定三角形三个顶点坐标，示例：((ax,ay),(bx,by),(cx,cy))。:param depth: 指定层数"""a, b, c = triangledraw_triangle(a, b, c)if depth == 0:returnelse:d = get_midpoint(a, b)e = get_midpoint(b, c)f = get_midpoint(c, a)draw_sierpinski([a, d, f], depth-1)draw_sierpinski([d, b, e], depth-1)draw_sierpinski([f, e, c], depth-1)triangle = [[-200, -100], [0, 200], [200, -100]]
draw_sierpinski(triangle, 5)
p.draw()