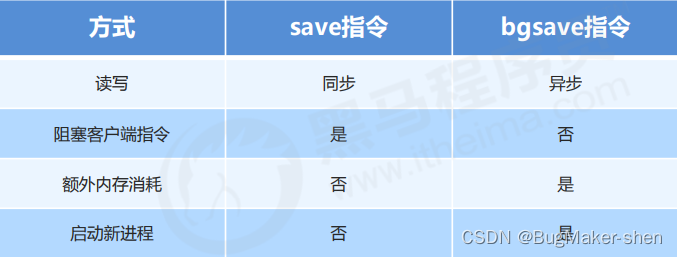
一、 问题描述

类似于分形树，分形三角形——谢尔宾斯基三角形同样是一种分形，由波兰数学家谢尔宾斯基在1915年提出。它是自相似集的例子。它的豪斯多夫维是log(3)/log(2) ≈ 1.585。对于谢尔宾斯基三角形的构造，可以先作一个正三角形，挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用黑色三角形代表挖去的面积，那么白三角形为剩下的面积（我们称白三角形为谢尔宾斯基三角形）。如果用上面的方法无限连续地作下去，则谢尔宾斯基三角形的面积越趋近于零，而它的周长越趋近于无限大。

二、问题分析

在分形树——python递归中，因为分形图形每个部分都具有相同形状，因而我们从最基本的情况开始考虑。

这里，我们先定义try_1(),用turtle按第一个图案所示顺序画出“度”为1的三角形;接着定义tri_2()，即在三个正放的小三角形顶点处调用tri_1();同理定义tri_3()。我们很容易的可以想到递推关系——在“度”为n的三个正放的小三角形顶点处调用函数tri_n-1()，于是便可以画出图示谢尔宾斯基三角形。

三、算法设计

import turtlet = turtle

tri_1()、tri_2()、tri_3()

def tri_1(sd_le=200):	# se_le = side lenth 表示边长"""图示顺序画出三角形"""t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le)t.left(120)t.forward(sd_le)t.right(120)def tri_2(sd_le=200):	"""画出'度'为2的三角形"""tri_1(sd_le // 2)t.right(120)t.forward(sd_le / 2)t.left(120)tri_1(sd_le // 2)	# 调用tri_1()t.forward(sd_le / 2)tri_1(sd_le // 2)t.right(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le)t.left(120)t.forward(sd_le)t.right(120)def tri_3(sd_le=200):"""画出'度'为3的三角形"""tri_2(sd_le // 2)t.right(120)t.forward(sd_le / 2)t.left(120)tri_2(sd_le // 2)	# 调用tri_2()t.forward(sd_le / 2)tri_2(sd_le // 2)t.right(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le)t.left(120)t.forward(sd_le)t.right(120)

tri()

def tri(n, sd_le=200):	# se_le = side lenth 表示边长if n == 1:t.width(de * 7)t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le)t.left(120)t.forward(sd_le)t.right(120)else:t.width(de * 7)tri(n - 1, sd_le // 2)t.right(120)t.forward(sd_le / 2)t.left(120)tri(n - 1, sd_le // 2)t.forward(sd_le / 2)tri(n - 1, sd_le // 2)t.right(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le)t.left(120)t.forward(sd_le)t.right(120)

和分形树一样，分形三角形的最内层实际上并没有下一层，于是最内层的调用和else下的方法相同，tri()可以优化为：

def tri(n, sd_le=600):	# se_le = side lenth 表示边长if n > 0:tri(n - 1, sd_le // 2)t.right(120)t.forward(sd_le / 2)t.left(120)tri(n - 1, sd_le // 2)t.forward(sd_le / 2)tri(n - 1, sd_le // 2)t.right(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le)t.left(120)t.forward(sd_le)t.right(120)else:pass

四、完整代码

import turtlet = turtle
t.hideturtle()
t.speed(999)
t.color('grey')
t.width(3)
t.penup()
t.goto(0, 300)
t.pendown()def tri(n, sd_le=600):if n > 0:tri(n - 1, sd_le // 2)t.right(120)t.forward(sd_le / 2)t.left(120)tri(n - 1, sd_le // 2)t.forward(sd_le / 2)tri(n - 1, sd_le // 2)t.right(120)t.forward(sd_le / 2)t.right(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le / 2)t.left(120)t.forward(sd_le)t.left(120)t.forward(sd_le)t.right(120)else:passtri(5)
t.done()

五、运行结果