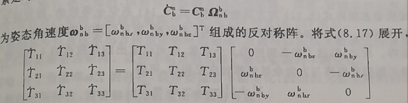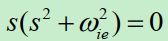捷联式惯导与平台式惯导最本质的区别在于用数学平台代替物理平台

捷联式惯导概要

捷联式惯导的加速度计是直接装在载体上的，得出的是载体坐标系（b系）内的数据，但是载体坐标系不能当作导航坐标系。

捷联式系统加速度计测得的比力分量如下
$$f^b=\left[\begin{array}{c}{f}_x^b\\ f_y^b\\ f_z^b\end{array}\right]$$

只有将$f^b$转到$f^n$(导航坐标系n系)，才能把载体的水平加速度和重力加速度分开，以进行有效的地表导航。b系到n系公式如下：

$$f^n=C_b^n{f}^b$$
因此计算机必须能实时地提供方向余弦矩阵$C_b^n$，才能实现转换。
为了实时地提供方向余弦矩阵$C_b^n$，就必须解以下微分方程组：

$$C{}^{\prime }={\Omega }_{nb}^b{C}_b^n$$
${\Omega }_{nb}^b$ 为：

在捷联式惯导系统中，还有3个陀螺安装在载体上，他们的测量轴分别与载体坐标系b的3个轴重合，这样他们可以测得载体相对惯性空间的角速度$w_{ib}^b$,下面的ib表示b系到i系，上面的b表示在载体坐标系测量的结果。

需要将$w_{ib}^b$转换为$w_{nb}^n$,因为上式的${\Omega }_{nb}^b$是在nb两个系中的变量。
转换方程如下：
$$w_{ib}^n=C_b^n{w}_{ib}^b$$
上式表示载体坐标系载体相对于惯性空间的角速度经过变换后得到导航坐标系载体相对于惯性空间的加速度
$$w_{nb}^n=w_{ib}^n-w_{in}^n=w_{ib}^n-(w_{ie}^n+w_{en}^n)$$
上式中$w_{in}^n$为导航坐标系相对惯性空间的角速度。$w_{ie}^n$ 与$w_{en}^n$分别为地球自身角速度和到导航坐标系相对地球的角速度

$w_{ib}^b$可以测得，$w_{ie}^n$与$w_{en}^n$与$C_b^n$需要提供。

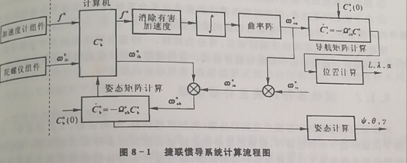
图太渣了，以后有时间自己画一个

惯性器件的误差补偿原理
找了一张图，完美的解释了补偿原理

捷联式惯导系统基本力学方程式两个矩阵微分方程（导航位置方程和姿态方程）。载体位置和状态都是在不断变化的，因此，在解两个矩阵微分方程时，要求提供相应的位移角速率和姿态速率方程。

1.捷联式惯导的基本力学编排方程

1.捷联式惯导系统的原理框图

上图中的p既是n导航坐标系
姿态速度方程为：$$C{}^{\prime }={\Omega }_{nb}^b{C}_b^n$$
$w_{nb}^b$时姿态矩阵的速率。
姿态矩阵的速率方程需要转换到载体坐标系中运算：
$$w_{nb}^b=w_{ib}^b-C_n^b{w}_{in}^n=w_{ib}^n-C_n^b(w_{ie}^n+w_{en}^n)$$
与上面的相似的方程区别时在载体坐标系b系
位移角速率为$w_{en}^n$，它在位置方程中由位移角速率方程求得。

2 .姿态方程

实现机体坐标系至导航坐标系转换的捷联矩阵$C_b^n$应满足如下的矩阵方程：$$\left[\begin{array}{c}{x}_n\\ y_n\\ y_n\end{array}\right]=C_b^n\left[\begin{array}{c}{x}_b\\ y_b\\ y_b\end{array}\right]$$
由于方向余弦阵$C_b^n$是正交矩阵，因而$C_b^n=[C_n^b{]}^{-1}=[C_n^b{]}^T$,令$$C_b^n=\left[\begin{array}{ccc}{T}_{11}& T_{12}& T_{13}\\ T_{21}& T_{22}& T_{23}\\ T_{31}& T_{32}& T_{33}\end{array}\right]$$
于是
$$C_b^n=\left[\begin{array}{ccc}cos\gamma cos\phi -sin\gamma sin\theta sin\phi & -cos\theta sin\phi & sin\gamma cos\phi +cos\gamma sin\theta sin\phi \\ cos\gamma sin\phi +sin\gamma sin\theta cos\phi & cos\theta cos\phi & sin\gamma sin\phi -cos\gamma sin\theta cos\phi \\ -sin\gamma cos\theta & sin\theta & cos\gamma cos\theta \end{array}\right]$$

由姿态矩阵确定飞行器姿态角
因为$C_b^n$是姿态角$\gamma ,\theta ,\phi$ 的函数。可得$\gamma ,\theta ,\phi$的主值为
$$\{\begin{array}{ll}& {\theta }_{mian}=arcsin{T}_{32}\\ & {\gamma }_{mian}=arctan\frac{-T_{31}}{T_{33}}\\ & {\phi }_{mian}=arctan\frac{-T_{32}}{T_{33}}\end{array}$$
因为姿态角有定义域，俯仰角$\theta$的定义域为（-90°，90°），偏航角$\gamma$为（-180°，180°）,横滚角$\phi$为（0°，360°）。

姿态矩阵微分方程
$C_b^n$ 是时间的函数。为求$C_b^n$ 需要求解姿态微分方程(姿态速率方程)$$C{}^{\prime }={\Omega }_{nb}^b{C}_b^n$$
上式中${\Omega }_{nb}^b$为姿态角速度$w_{nb}^b=[w_{nbx}^b,w_{nby}^b,w_{nbz}^b{]}^T$组成的反对称阵
将上式子展开如下

原谅这个矩阵方程写起来太复杂了，直接拍照上图。

可以看出，上图中对应9个一阶微分方程。只要给定初始值$\gamma ,\theta ,\phi$ ，在姿态角速率$w_{nb}^n$已知的情况下求解，即可确定姿态矩阵$C_b^n$ 中的元素值，进而确定飞行器的姿态角。

3.位置方程

位置矩阵$C_e^n$的计算
建立导航位置方程的目的，是为了确定载体的质心位置。由于所选导航坐标系的不同，因而质心位置的参数也略有不同，对指北方位系统是纬度$L$和经度$\lambda$；而对于游动方位系统就是$L,\lambda$和游动方位角$\alpha$。
下面介绍位置矩阵的推导
将地球系（e）到地理系（t）需要先绕Z轴转$90+\lambda$让X轴与地理系X轴重合，在绕X轴转动$90-L$使得Z轴与Y轴重合。于是方向余弦矩阵为$$C_e^t=\left[\begin{array}{ccc}-sin\lambda & cos\lambda & 0\\ -sinLcos\lambda & -sinLsin\lambda & cosL\\ cosLcos\lambda & cosLsin\lambda & sinL\end{array}\right]$$
又因为地理系(t)与导航系(n)之间差一个游动方位角$\alpha$，他们之间的方向余弦矩阵为$$C_t^n=\left[\begin{array}{ccc}cos\alpha & sin\alpha & 0\\ -sin\alpha & cos\alpha & 0\\ 0& 0& 1\end{array}\right]$$
所以地球系（e)到导航系（n）之间的方向余弦矩阵也就是位置矩阵$C_e^n$为$$C_e^n=C_t^n{C}_e^t$$
将上两式子导入展开得到：

嘿嘿，看图

位置矩阵$C_e^n$的计算
若想要求出对于的位置矩阵$C_e^n$，需要解$C_e^n$所对应的微分方程，即$$C_e^{n^{\prime }}=-{\Omega }_{en}^n{C}_e^n$$
式中${\Omega }_{en}^n$为位置角速率$w_{en}^n$的反对称阵。
考虑$w_{enz}^n=0$，则导航计算机要解算的微分方程为。
即可确定位置矩阵$C_e^n$中的元素值，进而确定导航位置参数。

位置角速率$w_{en}^n$方程

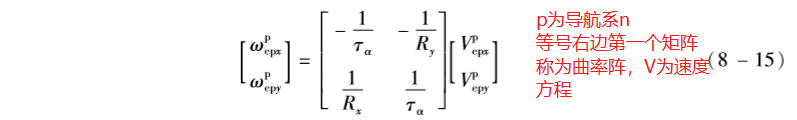
速度方程

垂直通道阻尼
与平台式一样

捷联式惯导系统的力学编排

2.捷联式惯导系统误差补偿与初始对准

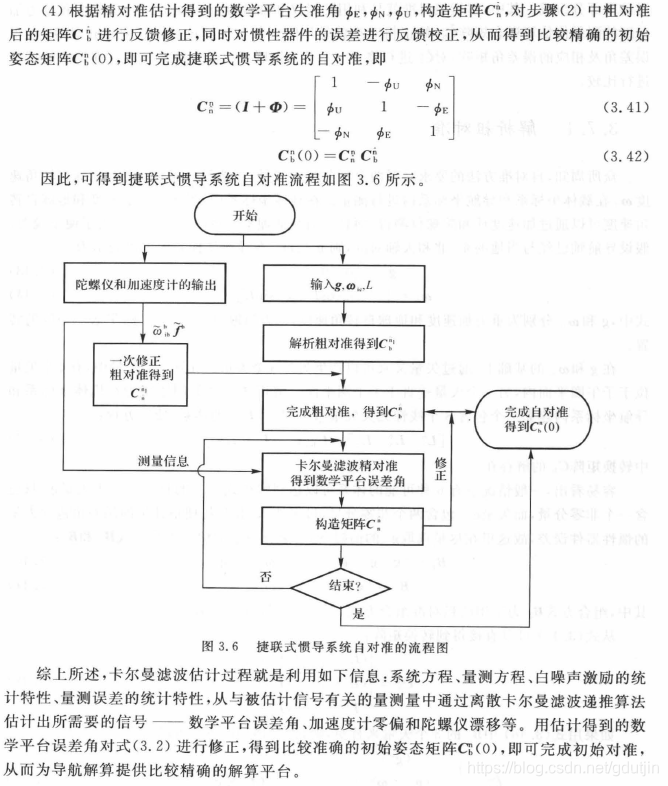
由于捷联矩阵$C_b^n$起到了平台的作用，因此导航工作一开始就需要获得捷联矩阵$C_b^n$的初始值，以便完成导航任务。显然，捷联式惯导系统的初始对准就是确定捷联矩阵的初始值。

陀螺仪和加速度计的误差会导致初始对准误差，初始对准时飞行器的干扰运动也是产生对准误差的重要因素。

2.1捷联式系统误差方程

“数学平台”的误差方程——姿态误差方程
在捷联式惯导系统中，机体姿态角是通过姿态矩阵（“数学平台”）计算出来的。在理想情况下，导航计算机计算的地理坐标系（$\hat{t}$ 表示） 应该和 真地理坐标系（t系） 一致。也就是导航计算机计算的姿态矩阵$\dot{C_b^t}$与理想姿态矩阵$C_b^t$。然而，由于系统存在 测量误差、计算误差和干扰误差等误差源，理想与计算得到的地理坐标系之间有偏差。
用姿态误差矢量角$\phi$ 表示理想与计算坐标系之间的误差

捷联式惯导系统中，姿态矩阵$C_b^t$是通过姿态微分方程$\dot{C_b^t}=C_b^t{\Omega }_{tb}^b$, 而${\Omega }_{tb}^b$取决于姿态角速率${\omega }_{tb}^b$（上式中t系可以理解为导航坐标系n）。在推导数学平台误差方程过程中，首先应该确定${\omega }_{tb}^b$，然后将矩阵微分方程（姿态微分方程）$\dot{C_b^t}=C_b^t{\Omega }_{tb}^b$变换成误差角$\phi$ 表征的姿态误差角方程。

设真地理系 $t$ 到计算地理系 $\hat{t}$ 的方向余弦矩阵为 $C_t^{\hat{t}}$ ,由于他们之间相差仅一个小角度$\phi$ ,因此有$$C_t^{\hat{t}}=\left[\begin{array}{ccc}1& {\phi }_z& -{\phi }_y\\ -{\phi }_z& 1& {\phi }_x\\ {\phi }_y& -{\phi }_x& 1\end{array}\right]=I-{\Phi }^t$$
反之，计算地理系到真地理系的方向余弦矩阵为：$$C_{\hat{t}}^t=[C_t^{\hat{t}}{]}^T=I+{\Phi }^t$$
其中$${\Phi }^t=\left[\begin{array}{ccc}0& {\phi }_z& -{\phi }_y\\ -{\phi }_z& 0& {\phi }_x\\ {\phi }_y& -{\phi }_x& 0\end{array}\right]$$

太多太复杂，推导如下图






上式中$\Omega$表示地球自转角速率

速度误差方程
加速度计的输出中包含加速度计零偏和机体角运动引起的扰动输出

上式中$$\delta V_{epy}^G={\int }_{t_1}^{t_2}{a}_{iby}^{p}dt$$
$$\delta V_{epx}^G={\int }_{t_1}^{t_2}{a}_{ibx}^{p}dt$$
G代表真地理系，P代表计算地理系，【t1,t2】为计算步长。

位置误差方程

系统误差方程及简要分析

所谓是指计算与真实之差，而描述其变化的微分方程便是误差方程。