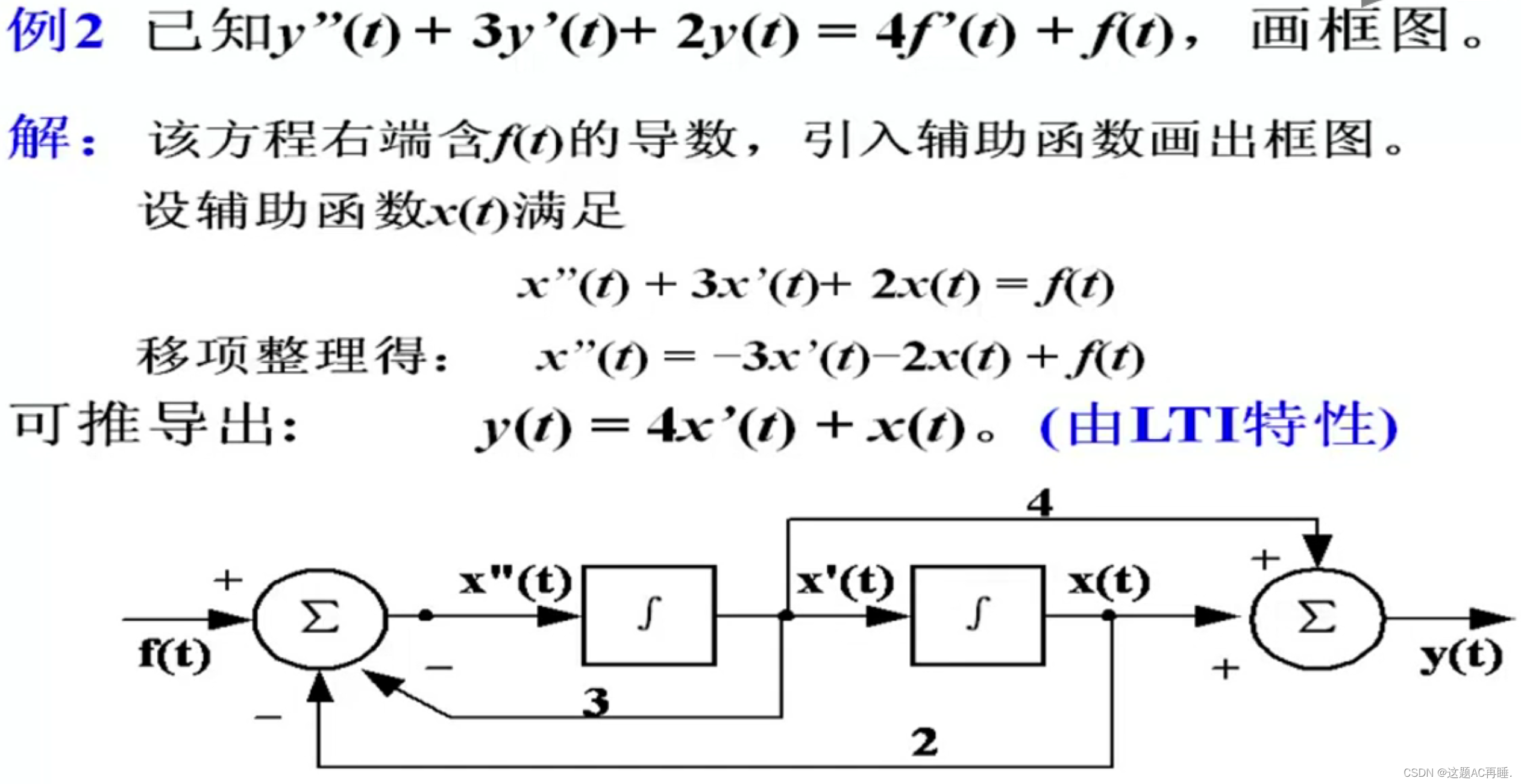
一、捷联惯导数值更新算法
导航坐标系:东-北-天
载体坐标系:右-前-上
1、姿态更新算法:
<1>姿态更新微分方程:

,表示导航系相对于惯性系的旋转;包括两部分:
(1)地球自转引起的导航系旋转;
(2)系统在地球表面附近移动因地球表面弯曲引起的导航系旋转;

根据矩阵链式乘法得:

又由于:
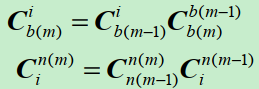
姿态微分方程:
![]()

<2>姿态更新方程:

对于,通过陀螺仪的积分可到,利用双子样圆锥补偿算法:

对于,认为短时间内速度和位置引起的
变化很小,将将
视为常值,则有:

注:此时的计算,取转置;
2、速度更新算法:
<1>速度更新微分方程:

为加速度计测量的比力;
为由载体运动和地球自转引起的哥式加速度;
为由载体运动引起的对地向心加速度;
为重力加速度;
统称为有害加速度;
<2>速度更新算法:
将微分方程,添加时间参数:

即:

和
分别称为时间段
内导航系比力速度增量和有害加速度的速度增量;
(1)
其中有害加速度的速度增量表达式,变化很小,直接采用中间时刻的值代替进行计算:,其中需要外推的量为:

(2)
采用矩阵链式乘法分解(与姿态更新算法一致)

即:

中间量为:


3、位置更新算法:
<1>位置微分方程:
![]()

<2>位置更新方程:


相关中间量为:

二、捷联惯导误差方程:
1、非直角坐标系到直角坐标系:
非直角坐标系α系:
直角坐标系b系:
从α系到b系到坐标变换矩阵为:

易知的列向量为单位矢量,但行向量一般不是单位矢量,在矩阵
中仅有6个独立元素;
近似如下:

对上述的进行正交三角分解(QR分解):分解为单位正交阵
和上三角阵
乘积的形式:
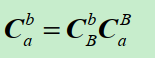
<1> 看作是从b系(直角坐标系)到另一右手直角坐标系(B系)的变换矩阵,(失准角)
若记从b系到B系的失准角(等效旋转矢量)为μ:

<2>上三角阵表示从非直角坐标系(a系)至直角坐标系(B系)的坐标变换矩阵:(偏差角/不正交误差角)

假设:α系的轴与B系的
轴重合;α系的
轴在B系的
平面内,且单位矢量
的端点在
和
轴上的投影分别记为
和
,α系的单位矢量
的端点在
、
、
轴上的投影分别记为:
、
、
。

简化,如下:

式中,φ表示矢量,构成的上三角阵,即:

最终如下:分别为 失准角和不正交角

注:失准角:两个直角坐标系之间的旋转小角度;
不正交角:从非直角坐标系到直角坐标系旋转小角度;
2、惯性传感器测量误差:
以三轴陀螺仪为例,陀螺仪输出的是某一个非直角坐标系(记为系);

其中,是从非直角坐标系(
)到直角坐标系b系的坐标变换矩阵;

3、姿态误差方程;
<1> 理想导航坐标系
为:从导航坐标系(n系)到载体坐标系(b系)的捷联惯导姿态矩阵;
<2> 计算导航坐标系
为:导航计算机解算给出的姿态矩阵;简记:系;
因此,与
之间的偏差在于
系与
系之间的偏差。
根据矩阵链乘规则:

以系为参考坐标系,从
到
系的等效旋转矢量为Φnn',常称其为失准角误差。
![]()
转置后:
![]()
则n‘系下为:
![]()
--%%-- --%%-- --%%-- --%%-- --%%-- --%%-- --%%-- --%%-- --%%-- --%%-- --%%-- --%%-- --
推导姿态误差方程:
理想下,姿态矩阵微分方程:
![]()
实际下,姿态矩阵微分方程:

其中,陀螺仪测量误差、导航系计算误差,都包含在以下中:
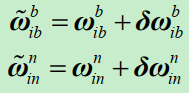
最终姿态误差微分方程为:
![]()
反映了计算导航系(系)相对于理想导航系(
系)的失准角变化规律。
4、速度误差方程:
速度误差是指惯导系统导航计算机中的计算速度与理想速度之间的偏差;通过速度误差微分方程描述:
速度误差:
![]()
两边求微分:
![]()
其中,速度微分方程为:
![]()

中间量:
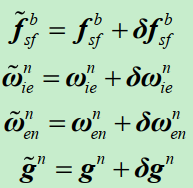
最终,速度误差微分方程为:

5、位置误差方程:
其中,Rm、Rn在短时间内变化很小,视为常值:

三、静基座误差特性分析:
静止基座下,惯导真实速度为0,真实位置已知;比力在导航坐标系的投影为[0 0 g]
将Rmh、Rnh近似为地球平均半径R;
1、高度通道
高度误差微分方程和天向速度误差微分方程:

高度误差会随时间不断发散,因此,纯惯导系统的高度通道是不稳定的;
2、水平通道误差微分方程:
经度误差δλ的传播是一个独立过程,仅收东向速度误差δVe的一次积分,不受其他误差影响;

修拉角频率:
傅科角频率: ,即为地球自转的天向分量;
如果取g=9.8,R=6371km;
可得到休拉周期;
傅科周期:在地区极点处最短为24小时,随纬度较小,周期变长,傅科周期在赤道上消失;因此,总有
3、水平通道简化
<1>单纯的失准角误差通道:
假设:水平两个速度误差为0,纬度误差为0;
单纯的姿态误差方程式为:

可视为:固定地理位置下的姿态跟踪误差方程;系统的特征方程为:
![]()
可得:单纯的失准角回路的震荡频率为地球自转频率,周期24Hour。
<2>水平东向/北向通道
<3>水平北向及方位通道