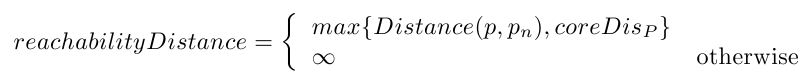基于密度的聚类算法（2）——OPTICS详解

article/2025/9/30 15:07:14

基于密度的聚类算法（1）——DBSCAN详解
基于密度的聚类算法（2）——OPTICS详解
基于密度的聚类算法（3）——DPC详解

1. OPTICS简介
  上一节介绍的DBSCAN算法中，较小的eps将建立更多的簇，而较大的eps将吞并较小的簇建立更大的簇。而OPTICS（Ordering Points to identify the clustering structure）算法，翻译为对点排序以确定簇结构，是对DBSCAN的一种优化，可以理解为将eps从单个值放宽到范围值。

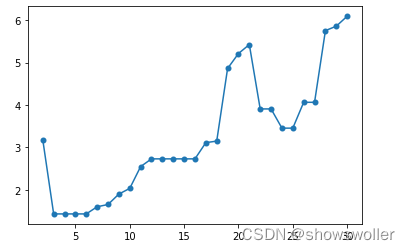
  OPTICS是DBSCAN聚类的改进算法，其对输入参数不敏感。此外，对只要确定minPts的值，半径eps的轻微变化，并不会影响聚类结果。OPTICS并不显式产生聚类簇，而是生成一个增广的簇排序（比如，以可达距离为纵轴，样本点输出次序为横轴的坐标图），这个排序代表了各样本点基于密度的聚类结构，从此排序中可以得到基于任何参数eps和minPts的DBSCAN算法的聚类结果。

OPTICS聚类：有效的解决了密度不同导致的聚类效果不好的问题。

核心距离：只有核心对象才有核心距离，在核心对象中，最小邻域内密度达到阈值时的半径值。 如果样本的核心距离小于半径则为核心点，否则不是核心点。

可达距离：只有核心对象才有可达距离，用于对样本点排序；

聚类顺序 : 从 低层 到 高层 ; 从 稠密 到 稀疏 ;

聚类时 , 低层 聚类分组 先构建完成 , 也就是半径 ε 参数较小的聚类分组 ;

密度可达的两种情况情况 :

① ε 参数小 : ε 参数较小的时两个样本就密度可达 ;

② ε 参数大 : ε 参数取值很大时 , 才密度可达 ;

扩展样本优先级 : 扩展样本对象时 , 优先选择第一种情况 , ε 参数较小的时就可密度可达的样本 ;

每个样本对象需要存储两个值 : 核心距离 与 可达距离 。

2. OPTICS算法流程及python、matlab代码实现：

(1) 创建两个队列，有序队列和结果队列。

  1. 有序队列用于存储core points及其密度直达points, 并按可达距离升序排列。有序队列中的points为待处理样本；

  2. 结果队列用于存储样本点的输出次序。结果队列中的points为处理之后的样本；

(2) 选取一个未处理的core point, 将其放入结果队列，同时计算邻域内样本点的可达距离，按照可达距离升序将样本点依次放入有序队列。

(3) 若有序队列为空，则回到步骤2（重新选取处理数据）。否则，从有序队列中提取第一个样本，如果为core point, 则计算可达距离，将可达距离最小的点放入结果队列。如果不是core point, 则重复步骤2；

  1. 如果有序队列中已经存在直接密度可达点，如果此时新的可达距离小于旧的可达距离，则用新可达距离取代旧可达距离，有序队列重新排序(因为一个对象可能有多个核心对象可达)；

  2. 如果有序队列中不存在该直接密度可达样本点，则插入该点，并对有序队列重新排序；

(4) 迭代(2)，(3)，直到数据集中所有点都处理完成，则算法结束，输出结果队列中有序样本点。

可以从python 的sklearn库中调用OPTICS 函数：
class sklearn.cluster.OPTICS(min_samples=5, max_eps=inf, metric=‘minkowski’, p=2, metric_params=None, cluster_method=‘xi’, eps=None, xi=0.05, predecessor_correction=True)

from sklearn.cluster import OPTICS
import numpy as np
X = np.array([[1, 2], [2, 5], [3, 6], [8, 7], [8, 8], [7, 3]])
clustering = OPTICS(min_samples=2).fit(X)
clustering.labels_
array([0, 0, 0, 1, 1, 1])

此外， 在matlab中OPTICS函数为：

% [RD,CD,order]=optics(x,k)
% -------------------------------------------------------------------------
% Aim: 
% Ordering objects of a data set to obtain the clustering structure 
% -------------------------------------------------------------------------
% Input: 
% x - data set (m,n); m-objects, n-variables
% k - number of objects in a neighborhood of the selected object
% (minimal number of objects considered as a cluster)
% -------------------------------------------------------------------------
% Output: 
% RD - vector with reachability distances (m,1)
% CD - vector with core distances (m,1)
% order - vector specifying the order of objects (1,m)
% -------------------------------------------------------------------------
% Example of use:
% x=[randn(30,2)*.4;randn(40,2)*.5+ones(40,1)*[4 4]];
% [RD,CD,order]=optics(x,4)
% -------------------------------------------------------------------------
% References: 
% [1] M. Ankrest, M. Breunig, H. Kriegel, J. Sander, 
% OPTICS: Ordering Points To Identify the Clustering Structure, 
% available from www.dbs.informatik.uni-muenchen.de/cgi-bin/papers?query=--CO
% [2] M. Daszykowski, B. Walczak, D.L. Massart, Looking for natural  
% patterns in analytical data. Part 2. Tracing local density 
% with OPTICS, J. Chem. Inf. Comput. Sci. 42 (2002) 500-507
% -------------------------------------------------------------------------
% Written by Michal Daszykowski
% Department of Chemometrics, Institute of Chemistry, 
% The University of Silesia
% December 2004
% http://www.chemometria.us.edu.plfunction [RD,CD,order,D]=optics(x,k)[m,n]=size(x);  % m=70,n=2
CD=zeros(1,m);
RD=ones(1,m)*10^10;% Calculate Core Distances
for i=1:m    D=sort(dist(x(i,:),x));CD(i)=D(k+1);   % 第k+1个距离是密度的界限阈值
endorder=[];
seeds=[1:m];ind=1;while ~isempty(seeds)ob=seeds(ind);%disp(sprintf('aaaa%i',ind))seeds(ind)=[];      order=[order ob];   % 更新ordervar1 = ones(1,length(seeds))*CD(ob);var2 = dist(x(ob,:),x(seeds,:));mm=max([var1;var2]);    % 比较两个距离矩阵，选择较大的距离矩阵ii=(RD(seeds))>mm;RD(seeds(ii))=mm(ii);[i1 ind]=min(RD(seeds));%disp(sprintf('bbbb%i',ind))
end   RD(1)=max(RD(2:m))+.1*max(RD(2:m));function [D]=dist(i,x)% function: [D]=dist(i,x)
%
% Aim: 
% Calculates the Euclidean distances between the i-th object and all objects in x     
% Input: 
% i - an object (1,n)
% x - data matrix (m,n); m-objects, n-variables        
%                                                                 
% Output: 
% D - Euclidean distance (m,1)[m,n]=size(x);
D=(sum((((ones(m,1)*i)-x).^2)'));   % 距离和if n==1D=abs((ones(m,1)*i-x))';
end

3. OPTICS的应用
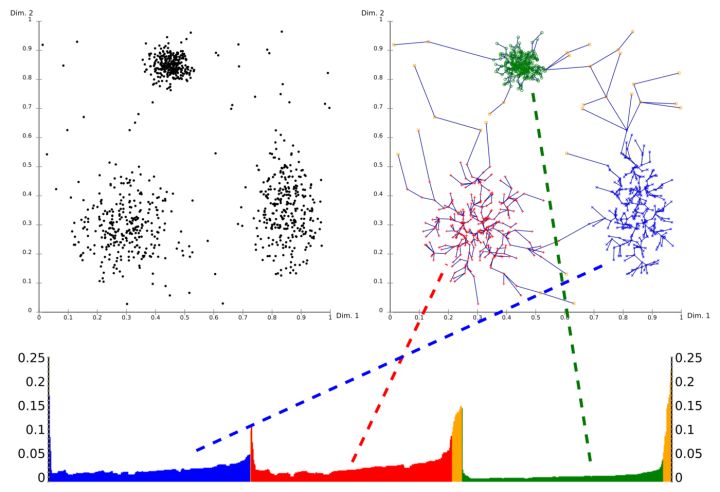
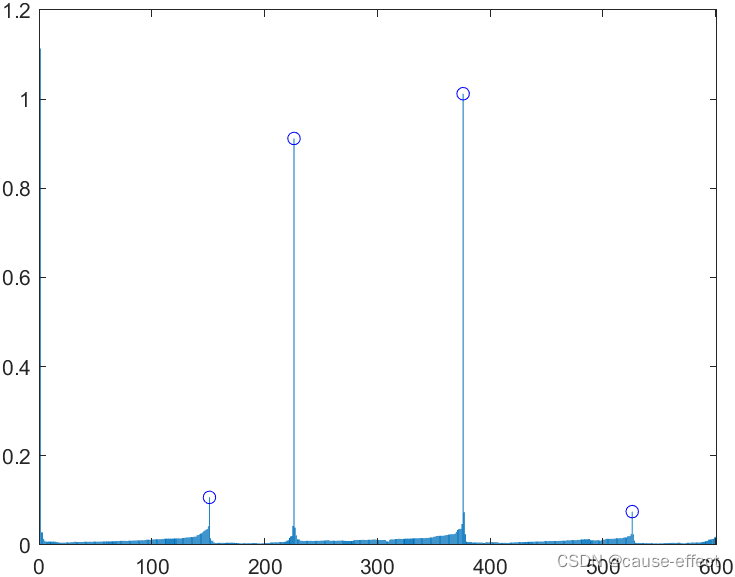
利用OPTICS聚类算法，无需预先确定聚类数目；而且还可以根据计算的结果（可达距离的分布）来看出密度结构，以分析自动确定的聚类数目的合理性。
下面给出一组结果（做了一些可视化工作），以显示OPTICS 聚类算法的效果：

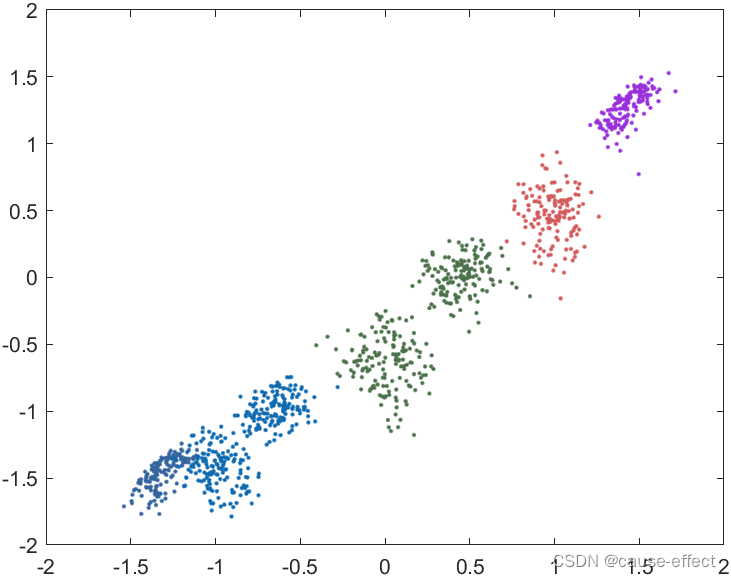
在这里插入图片描述

4. 总结

OPTICS是基于DBSCAN改进的一种密度聚类算法，对参数不敏感。当需要用到基于密度的聚类算法时，可以作为DBSCAN的一种替代的优化方案，以实现更优的效果。


http://chatgpt.dhexx.cn/article/3JJnFqvk.shtml

相关文章

【Python机器学习】密度聚类DBSCAN、OPTICS的讲解及实战演示（附源码 超详细）

【Python机器学习】密度聚类DBSCAN、OPTICS的讲解及实战演示（附源码 超详细）

需要源码和数据集请点赞关注收藏后评论区留言私信~~~ 划分聚类、密度聚类和模型聚类是比较有代表性的三种聚类思路 1：划分聚类 划分（Partitioning）聚类是基于距离的，它的基本思想是使簇内的点距离尽量近、簇间的点距离尽量远。k…
阅读更多...
OPTICS

OPTICS

OPTICS 就是一种基于密度的聚类算法，可以认为是dbscn的改进，改进之处主要是在不用每次调节eps和minpts都需要重新整个训练。其本质还是dbscan，只是能够在给定eps和minpts后，可以训练一次就可以在minpts值定对的情况下，…
阅读更多...
聚类算法初探（六）OPTICS

聚类算法初探（六）OPTICS

第一章 引言 第二章 预备知识 第三章 直接聚类法 第四章 K-means 第五章 DBSCAN 第六章 OPTICS 第七章 聚类分析的效果评测 第八章 数据尺度化问题 作者: peghoty 出处: http://blog.csdn.net/itplus/article/details/10089323 欢迎转载/分享, 但请务必声明文章出处. 转…
阅读更多...
OPTICS聚类（最清晰解释）

OPTICS聚类（最清晰解释）

背景 想要理解该算法，你需要先了解： DBSCAN算法 OPTICS（用于识别聚类结构的排序点）算法与 DBSCAN 算法有许多相似之处，可视为 DBSCAN 的泛化，将 eps 要求从单个值放宽到一个范围 DBSCAN 和 OPTICS 之间的主…
阅读更多...
机器学习笔记（十一）聚类算法OPTICS原理和实践

机器学习笔记（十一）聚类算法OPTICS原理和实践

OPTICS聚类算法是基于密度的聚类算法，全称是Ordering points to identify the clustering structure。提到基于密度的聚类算法，应该很快会想到前面介绍的DBSCAN聚类算法，事实上，OPTICS也是为了优化DBSCAN而出现的。 一、原理 在…
阅读更多...
sklearn聚类之OPTICS算法

sklearn聚类之OPTICS算法

文章目录 简介sklearn实现cluster_optics_dbscan 简介 OPTICS算法，全称是Ordering points to identify the clustering structure，是一种基于密度的聚类算法，是DBSCAN算法的一种改进。 众所周知，DBSCAN算法将数据点分为三类&…
阅读更多...
聚类算法——OPTICS

聚类算法——OPTICS

网上很多关于OPTICS算法的资料，学习了很多博客之后总感觉不太合自己口味，因此整理了一篇博文供总结和复习，如能有幸帮助到其他人便是荣幸之至，如有错误，不吝指出。阅读此文需要了解“聚类”，“基于密度聚类…
阅读更多...
JS获取url参数（简单、实用）

JS获取url参数（简单、实用）

// js获取url传参参数function GetQueryString(name) {var reg new RegExp("(^|&)" name "([^&]*)(&|$)");// Location 对象是 Window 对象的一个部分，可通过 window.location 属性来访问。var r window.location.search.substr(…
阅读更多...
js获取url参数值的两种方式详解

js获取url参数值的两种方式详解

有个url如下： http://passport.csdn.net/account/login?fromhttp%3a%2f%2fwrite.blog.csdn.net%2fpostedit 我们该如何获取from这个参数的值呢？在网上搜了下方法很简单，如下，第一种是通过正则，第二种通过切串放进数…
阅读更多...
js获取url参数值的方法总结

js获取url参数值的方法总结

js获取url参数值的方法总结 1、方式一：通过字符串截取的方式获取参数值；2、方式二：通过正则获取到参数值； 1、方式一：通过字符串截取的方式获取参数值； 1）、函数一：获取URL中的参数名…
阅读更多...
Hyperlynx学习心得

Hyperlynx学习心得

1、Altium Designer文件导入Hyperlynx问题 众所周知AD的文件各大友厂商的文件对它都不咋友好~，很多SI、PI文件都不支持，但AD可以输出Hyperlynx文件供其使用、但也会存在一些问题。我遇到问题就是 AD中使用填充的铜皮在Hyperlynx中不识别，直接…
阅读更多...
HyperLynx（二十五）电源完整性之直流压降分析（二）

HyperLynx（二十五）电源完整性之直流压降分析（二）

1.后仿真的直流压降 2.批量直流压降分析 3.如何改善电压下降较多的设计 1.后仿真的直流压降 (1)打开HperLynx软件。从目录中打开 C:\PI_Trng\lab2\exer2\ post_dc_drop.hyp，单击“Open”按钮，当打开板子时被问到是否用Man- hattan-style布线连接没有布…
阅读更多...
HyperLynx（二十二）DDR（五）DDRx总线时序模型设计

HyperLynx（二十二）DDR（五）DDRx总线时序模型设计

由于DDRx总线对时序的要求非常严格，随着速率的提升，时序的要求会更高。要使用DDRx批处理仿真器，需要创建控制器和DRAM颗粒的时序模型，时序模型文件后缀为“*.V”。 HyperLynx 提供两种方式进行时序模型的创建和编辑: 一种是在语…
阅读更多...
HyperLynx（八）带状线串扰的仿真

HyperLynx（八）带状线串扰的仿真

1. 前面介绍的是微带线的串扰仿真，其实带状线的串扰与微带线的串扰有比较大的不同。主要是在拓扑结构中传输线TL2和TL5为带状线，分布在第三层，微带线与带状线通过过孔连接。带状线的仿真拓扑如图所示： 叠层信息如图所示&#xff…
阅读更多...
HyperLynx（二十八）板层噪声分析和SI/PI联合仿真实例

HyperLynx（二十八）板层噪声分析和SI/PI联合仿真实例

板层噪声分析和SI/PI联合仿真实例 1.前仿真噪声分析 2.后仿真噪声分析 3.设置和运行SI/PI联合仿真 4.执行信号过孔旁路分析 1.前仿真噪声分析 (1)从“开始”菜单中打开HyperLynx:“开始”→“所有程序”一“Mentor Graphics SDD”→“HyperLynx”→“HyperLynx Simulation S…
阅读更多...
基于Hyperlynx VX.2.5 的DDR3仿真之一：Verifying That the Software Recognizes Your Design Correctly

基于Hyperlynx VX.2.5 的DDR3仿真之一：Verifying That the Software Recognizes Your Design Correctly

这是一篇基于Mentor公司 Hyperlynx VX.2.5 仿真软件针对Xilinx ZYNQ 的ZC702 PCB上DDR3内存布局布线的信号完整性仿真分析。层叠结构设置，关键信号的仿真分析，有助于我们了解基于 Hyperlynx 对 DDR3 进行信号完整性仿真的整个流程。 首先我们从实际出发…
阅读更多...
HyperLynx（三十一）高速串行总线仿真（三）

HyperLynx（三十一）高速串行总线仿真（三）

高速串行总线仿真（三） 1.从一个多层板工程中验证串行通道 2.在多层板中设置连接器模型 1.从一个多层板工程中验证串行通道 在本例练习中，将集中研究从芯片到插件形成的串行发射通道，并分析它的性能。 (1)打开 HyperLynx 软件&a…
阅读更多...
HyperLynx（五）反射仿真

HyperLynx（五）反射仿真

1.反射仿真 1.学过物理的工程师都知道，光在传输过程中不在介质的表面会发生反射和折射现象，如图所示。同样，对于信号而言，信号在传递的的过程中，遇到阻抗不连续的点(不同的介质或不同的物理结构时)，一部分…
阅读更多...
HyperLynx（十八）DDR（一）DDR简介和DDR的数据仿真

HyperLynx（十八）DDR（一）DDR简介和DDR的数据仿真

1.DDR简介 2.DDR仿真概述 3.DDR数据仿真前的数据验证 4.DDR数据仿真具体步骤 1.DDR简介 DDR（双倍速率同步动态随机存储器）是一个内存名称，意思即双倍速率同步动态随机存储器，是内存的其中一种。 DDR 总线是由 SDRAM 发展而来的一…
阅读更多...
HyperLynx（三十）高速串行总线仿真（二）

HyperLynx（三十）高速串行总线仿真（二）

高速串行总线仿真（二） 仿真实例 1.探索多层板中的PCI-E串行通道 2.设置叠层以减小损耗 3.分析通道的不同配置对损耗的影响 4.检测驱动端规范 5.检查接收器规范 6.通过仿真得出整个通道的驱动约束限制 1.探索多层板中的PCI-E串行通道 在本节练习中&am…
阅读更多...
推荐文章

Copyright @ 2022~2023