1、变换矩阵

变换矩阵可以分解为缩放，旋转，平移矩阵的乘积：

M = T * R * S - 右手坐标系

当均匀缩放时，旋转和缩放可以交换顺序

缩放和平移不可以交换顺序

2、子坐标系与父坐标系

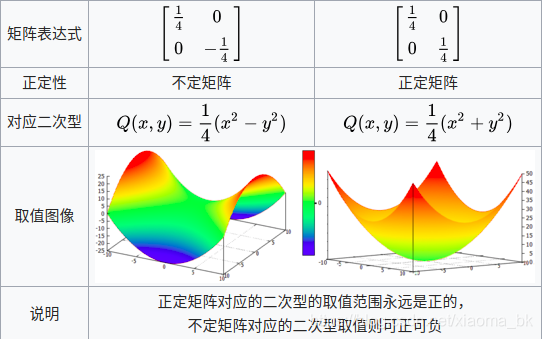
由在父坐标系中的坐标位置P，和三根轴X，Y，Z可定义一个子标系，按列构成一个变换矩阵[X,Y,Z,P]，这个矩阵构成由子标系变换到父坐标系的变换矩阵。DX里面需要转置一下。即按行构造。

一个例子是视图矩阵的构建，子空间由视点和三根正交轴定义，视图矩阵则是由它们构成的列矩阵的仿射求逆-由世界变换到视图空间。

另一个例子世界变换矩阵，它由新模型坐标系的位置和三根轴【定义在世界空间】按列构成。即由模型空间变换到世界空间。初始情况模型空间与世界空间是对齐的。

3、投影矩阵-OpenGL

透视投影矩阵：

可以知道投影变换后的w=-Ze，即在视图空间的深度

在投影面上的坐标Xp, Yp为：Xp=n*Xe/-Ze=Xclip/w*r，Yp=n*Ye/-Ze=Yclip/w*t

投影后Ze从[-n,-f]线性映射到[-n,f]，除以w后进一步非线性映射到[-1,1]

透视投影除以w后，视景体的八个角点【视图空间坐标】分别映射到NDC空间中的八个角点，如[r,t,-n,1]映射到[1,1,-1,1]，[f*r/n,f*t/n,-f,1]映射到[1,1,1,1]

正交投影矩阵：

变换后w=1，Xe，Ye，Ze被线性映射到-1~1，而透视投影是非线性映射，因而有Z-Fighting问题。

4.应用例子：从深度图重建位置

延迟渲染，SSR等特效都要求由深度信息重建位置信息，如果深度是归一化过的【0~1非线性】，可以将由纹理坐标uv[画一个全屏Quad]，深度z，计算出在NDC中的坐标，然后由投影矩阵逆变换，得到视图空间中的位置，这种情况会有精度损失，因为z是非线性的。解决办法是直接使用视图空间的深度，由uv可以得到NDC中的坐标[a,b,1,1]，逆变换到视图空间，得到ray=[a',b',f,1]，结合深度d，可以计算出坐标为d/f*ray。