内敛函数的定义：

以inline修饰的函数叫做内联函数，编译时C++编译器会在调用内联函数的地方展开，没有函数调用建立栈帧的开销，内联函数提升程序运行的效率

（它是以空间换取时间的方式提高效率，这里的空间指的是可执行程序的大小）

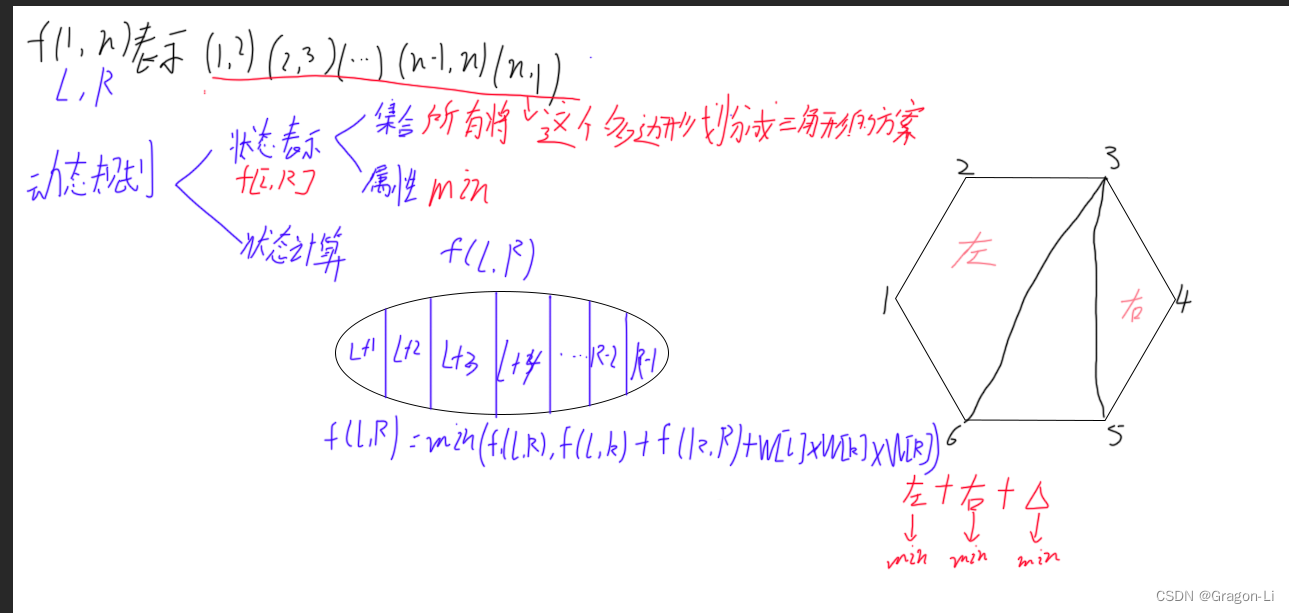
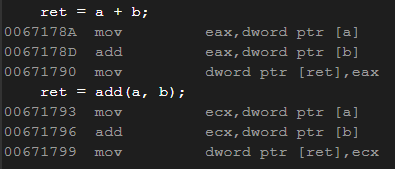
没有加inline时，在release优化后执行时会调用（call）函数

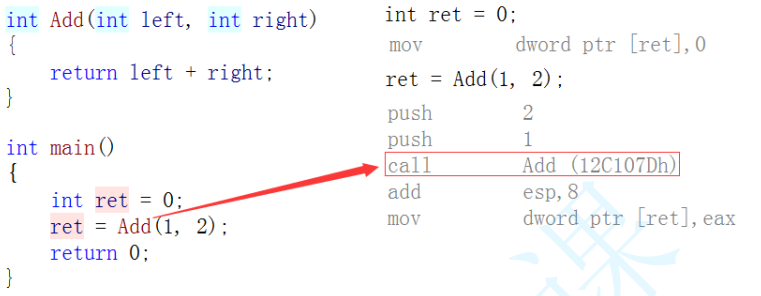
加inline后，在release优化后直接展开，不会再调用，调用几次展开几次

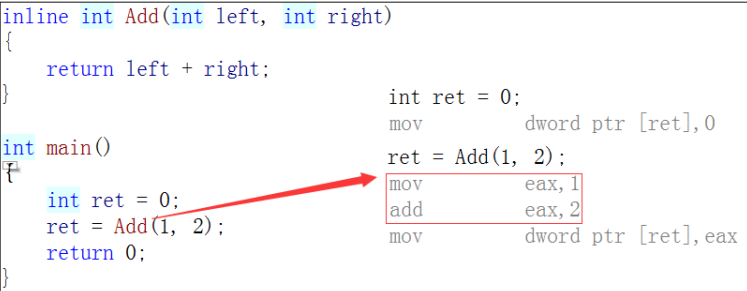
特性

1. inline是一种以空间换时间的做法，如果编译器将函数当成内联函数处理，在编译阶段，会用函数体替换函数调用，缺陷：可能会使目标文件变大，优势：少了调用开销，提高程序运行效率
   （比如函数体30行指令，需要调用1000次，没有inline下的指令数是1000+30行；有inline下的指令数是1000*30行，虽然少了栈帧的创建，但是可执行程序的空间变大）
2. inline对于编译器而言只是一个建议，不同编译器关于inline实现机制可能不同，一般建议：将函数规模较小(即函数不是很长，具体没有准确的说法，取决于编译器内部实现)、不是递归、且频繁调用的函数采用inline修饰，否则编译器会忽略inline特性。下图为《C++prime》第五版关于inline的建议：
   
   为什么代码长了不展开呢？
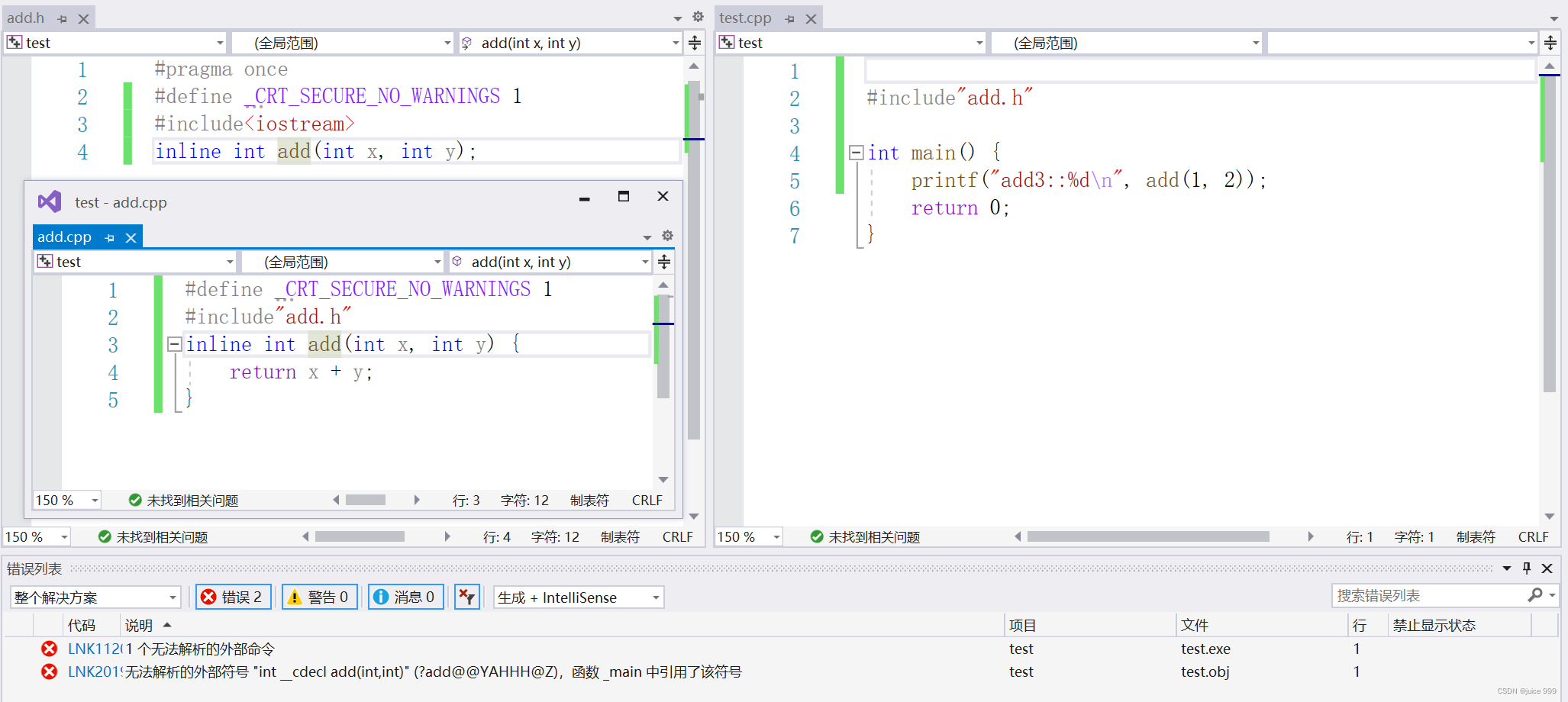
   展开后会使可执行程序大小变大。造成代码膨胀，不值得，编译器会自动识别函数长度再考虑要不要展开
3. inline不建议声明和定义分离，分离会导致链接错误。因为inline被展开，就没有函数地址了，链接就会找不到
   （在编译期间，会生成符号表，符号表中存放着函数的地址，在其他文件中引.h文件中函数的声明时，只要符合调用的规则，在编译期间并不会去其他文件找到对应的定义并开始调用，而是会在链接的时候将所有文件函数定义合并到一个符号表上，再根据函数名来找到对应的地址进行调用，但是如果inline修饰后的函数，函数的地址是进入符号表中的，这个时候只有声明没有定义，会出现函数未定义的错误）

XXX.h
int Add(int x, int y);XXX.cpp
#include "XXX.h"int Add(int x, int y)
{return x + y;
}test.cpp
#include <iostream>
#include "XXX.h"using namespace std;int main()
{int sum = Add(3, 4);cout << sum << endl;return 0;
}

所以直接把内联函数直接定义在.h头文件中，需要直接引入头文件，不要声明与定义分离

宏和内联函数

内联函数其实就是宏函数的优化后的产物，至于优化的地方就需要看一下宏的缺点

宏的缺点：

1. 不方便调试宏。（因为预编译阶段进行了替换）
2. 导致代码可读性差，可维护性差，容易误用
   正确：#define ADD(x,y) ((x)+(y))
   错误：#define ADD(x,y) (x+y)或#define ADD(x,y) x+y或#define ADD(x,y) ((x)+(y));
   对应使用ADD(1|0,1&1),ADD(2,3)*2,if(ADD(1,0));会出现符号优先级等问题
3. 没有类型安全的检查

宏的优点：

1. 增强代码的复用性
2. 提高性能

在C++中有两种方法来优化宏的缺点

4. 常量定义 换用const enum
5. 短小函数定义 换用内联函数