一、区别

转载自http://www.pythontab.com/html/2017/linuxkaiyuan_0115/1116.html

1. 由来

在计算机还没有出现之前，有一种叫做电传打字机（Teletype Model 33）的机械打字机，每秒钟可以打10个字符。但是它有一个问题，就是打完一行换行的时候，要用去0.2秒，正好可以打两个字符。要是在这0.2秒里面，又有新的字符传过来，那么这个字符将丢失。

于是，研制人员想了个办法解决这个问题，就是在每行后面加两个表示结束的字符。一个叫做“回车”，告诉打字机把打印头定位在左边界，不卷动滚筒；另一个叫做“换行”，告诉打字机把滚筒卷一格，不改变水平位置。

这就是“换行”和“回车”的由来。

2. 使用

后来，计算机发明了，这两个概念也就被般到了计算机上。那时，存储器很贵，一些科学家认为在每行结尾加两个字符太浪费了，加一个就可以。于是，就出现了分歧。

回车 \r 本义是光标重新回到本行开头，r的英文return，控制字符可以写成CR，即Carriage Return

换行 \n 本义是光标往下一行（不一定到下一行行首），n的英文newline，控制字符可以写成LF，即Line Feed

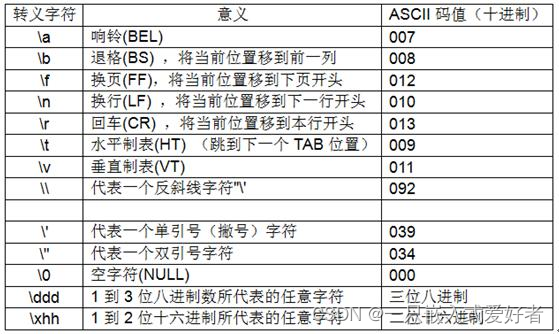
符号    ASCII码      意义

\n        10        换行NL

\r        13        回车CR

在不同的操作系统这几个字符表现不同，比如在WIN系统下，这两个字符就是表现的本义，在UNIX类系统，换行\n就表现为光标下一行并回到行首，在MAC上，\r就表现为回到本行开头并往下一行，至于ENTER键的定义是与操作系统有关的。通常用的Enter是两个加起来。

不同操作系统下的含义：

\n:  UNIX 系统行末结束符

\n\r: window 系统行末结束符

\r:  MAC OS 系统行末结束符

我们经常遇到的一个问题就是，Unix/Mac系统下的文件在Windows里打开的话，所有文字会变成一行；而Windows里的文件在Unix/Mac下打开的话，在每行的结尾可能会多出一个^M符号。

3. 软回车和硬回车

再扩展一下回车的一些知识。

硬回车就是普通我们按回车产生的，它在换行的同时也起着段落分隔的作用。 

软回车是用 Shift + Enter 产生的，它换行，但是并不换段，即前后两段文字在 Word 中属于同一“段”。在应用格式时你会体会到这一点。

软回车能使前后两行的行间距大幅度缩小，因为它不是段落标记，要和法定的段落标记——硬回车区别出来。硬回车的html代码是<p>..</p>，段落的内容就夹在里面，而软回车的代码很精悍：<br>。网页的文字如果复制到word中，则硬回车变为弯曲的箭头，软回车变为向下的箭头。

二、python中使用

转载自https://blog.csdn.net/mrknight/article/details/9717995

1. 测试程序（python2.7 +　win7）

（1） test1： "w"方式写时的'\n'会在被系统自动替换为'\r\n'

[python]  view plain copy

1. # -*- coding: utf-8  -*-  
2.   
3. def main():  
4.     try:  
5.         fout = open("test1.txt", "w")  
6.     except IOError:  
7.         print "Error: open file failed."  
8.         return  
9.   
10.     for i in range(5):  
11.         line = str(i) + "\n"  
12.         fout.write(line)  
13.   
14.     fout.close()  
15.   
16. if __name__ == "__main__":  
17.     main()  

测试结果：

（2） test2： "wb"方式写时的'\n'不会在被系统自动替换为'\r\n'

[python]  view plain copy

1. fout = open("test2.txt", "wb")  

测试结果：

（3） test3: "r"方式读时，文件中的'\r\n'会被系统替换为'\n'

另外，python提到的通用新行格式（U修饰符），个人觉得是把"r"默认"rU"的，测试中两种方式读取结果一样。

[python]  view plain copy

1. # -*- coding: utf-8  -*-  
2.   
3. def main():  
4.     try:  
5.         fin = open("test1.txt", "r")  
6.     except IOError:  
7.         print "Error: open file failed."  
8.         return  
9.   
10.     for line in fin:  
11.         for i in range(len(line)):  
12.             print "\t%d" % ord(line[i]),  
13.         print ""  
14.   
15.     fin.close()  
16.   
17. if __name__ == "__main__":  
18.     main()  

对于上述不同内容的两个文件输出为：

（4） test4： "rb"方式读时，文件中的'\r\n'不会被系统替换为'\n'