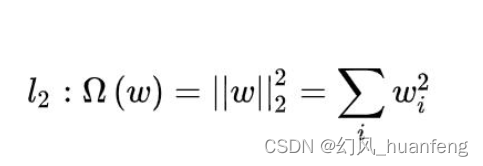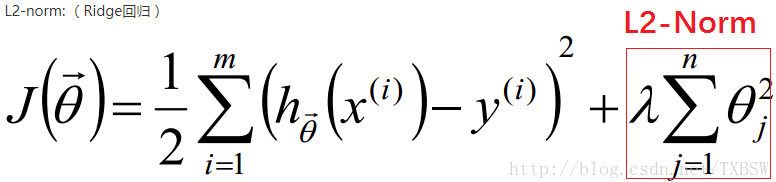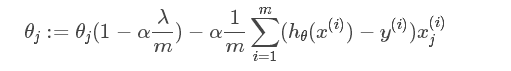1. L1正则化,也称Lasso回归
1.1 含义
权值向量 中各元素的绝对值之和,一般记作
。
1.2 公式表示
添加了L1正则化的损失函数一般可表示为:
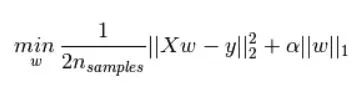
1.3 作用
L1正则常被用来解决过拟合问题;
L1正则化容易产生稀疏权值矩阵(更容易得到稀疏解),即产生一个稀疏模型(较多参数为0),因此也可用于特征选择。
1.4 为什么L1(相对L2)更容易获得稀疏解 或者 0解
L1是舍弃掉一些不重要的特征,L2是控制所有特征的权重。
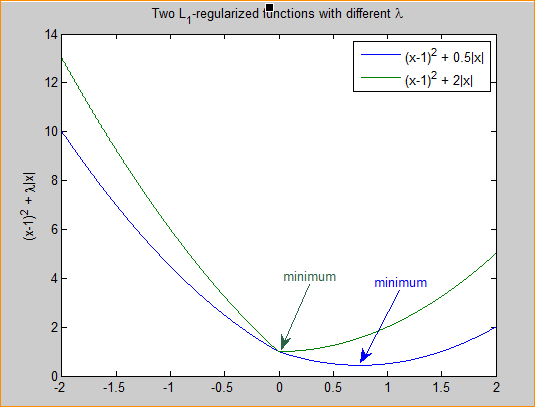
a. 从公式角度解释
假设只有一个参数 w,损失函数 L(w) , 分别加上L1和L2损失函数可得:
假设 L(w) 在 某一个样本 0 处 的导数是 d0
当结合L2正则时候的导数是:
当结合L1正则时候的导数是(L1损失在 w = 0处不可导,分 0 - 和 0 +):
结论:当结合L2正则的损失函数,导数结果仍然是 d0;结合L1正则的损失函数会有一个突变,从
到
,只要满足
或
和
异号,则在w = 0处,损失函数有极值(极小值),在优化器优化过程中,很容易将结果收敛到该极小值点上,也就是 w = 0。相比L1正则,需要 d0 = 0,这样的条件明显更为严苛。
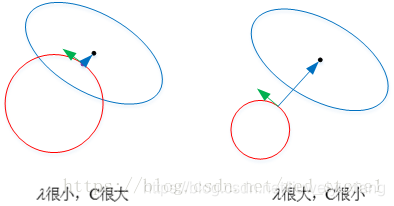
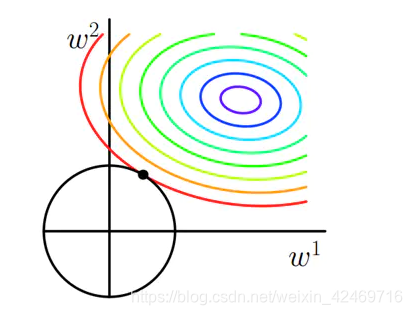
b. 从优化问题视角 + 二维图示例 + 多维扩展,方向解释

c. 从梯度角度来看

结论:加入L1正则的导数形式,无论 wi 大小如何,sgn(wi) 的结果是一个常数,因此惩罚力度不变或者说仍然很大,使得L1将参数惩罚到0的概率增加;反观L2正则的导数形式,在 wi < 1 时候,尾项惩罚作用小,很难将参数惩罚到0,实际上就是使每个特征都得到尽量均衡的权重,因此适用于解决普通的过拟合问题,即从参数分布(让分布尽可能的均匀)的角度解决过拟合的问题。
d. 从概率学角度
加入正则项,相当于对参数 w 增加先验假设,要求 w 满足某一种分布。
L1正则化相当于为 w 加入 “拉普拉斯分布” 的先验;L2正则化相当于为 w 加入 “高斯分布” 的先验。

结论:拉普拉斯先验在0点附近分布密度大于高斯分布,最终解将更稀疏。
2. L2正则化
2.1 含义
权值向量/矩阵 中各元素的平方和,然后对“和”求平方根,记作
。
2.2 公式表示
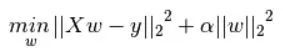
2.3 作用
L2正则化 可防止模型过拟合;至于为什么见下一篇文章,不定期更新
能够得到较为平滑(smooth)的解。
3. L1和L2正则化的适用场景
结论1 :从理论上来看,参数如果服从高斯分布就用L2正则化;服从拉普拉斯分布就用L1。
结论2 :添加正则化相当于参数的解空间添加了约束,限制了模型的复杂度,缓解过拟合。不过L1和L2正则化项是从不同的角度解决过拟合的。
结论3 :L1正则项是从改变模型结构的角度(减少模型参数的数量 或者 筛除无效特征,使无效特征对应的参数为0)解决过拟合,使的模型更加简单。
结论4 :L2正则项使模型尽量不依赖于某小部分特征,使模型更倾向于使用所有输入特征,不恰当的讲就是使每个特征都得到尽量均衡的权重(对于重要、非重要的特征也会有比较明显的区分);它是从参数分布(让分布尽可能的均匀)的角度解决过拟合。
结论5 :L1正则化可以获得稀疏解,因此适用于:模型剪枝、模型压缩、特征选择。
结论6 :L2正则化可以获得平滑(smooth)解。