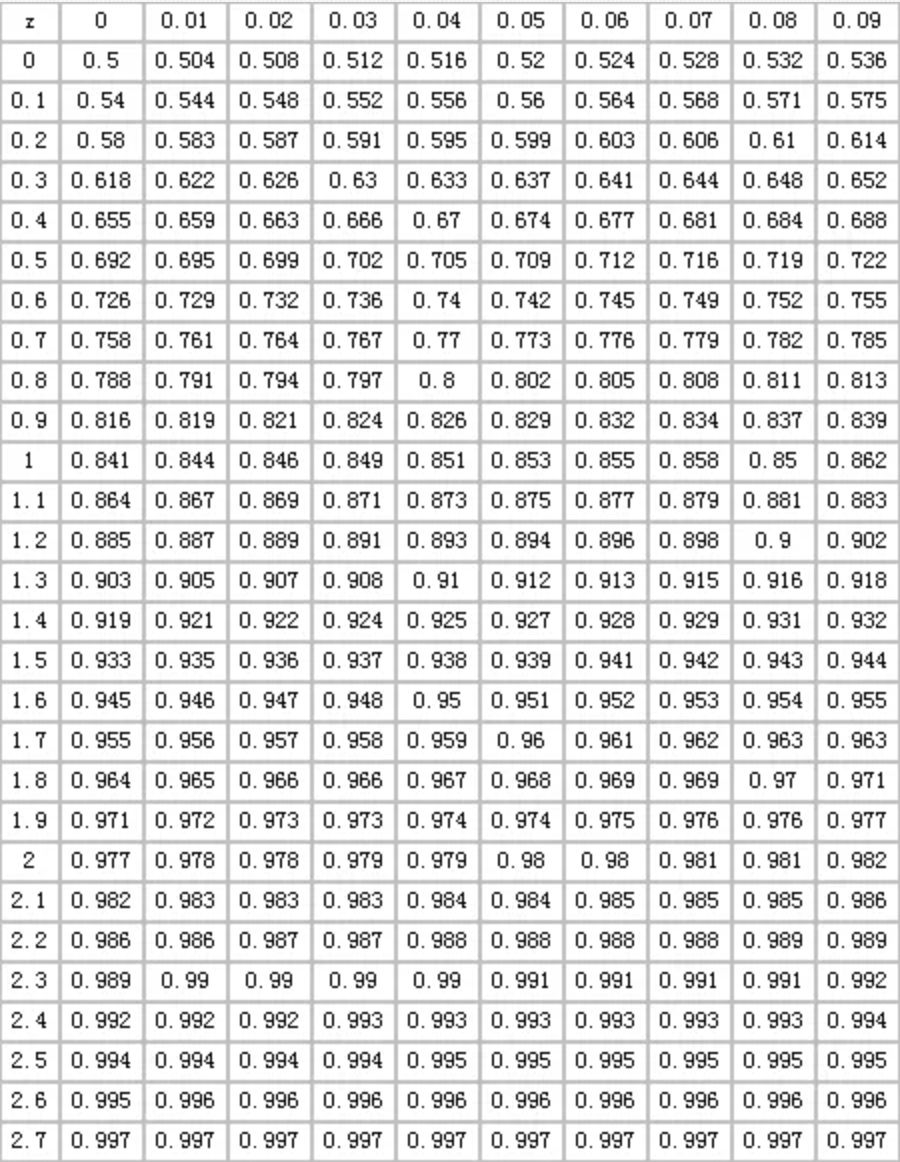
仿真输入之间的相关性
蒙特卡罗模拟的设计决策之一是为随机输入选择概率分布。为每个变量选择一种分布往往很简单,但确定输入之间应该存在什么样的相关性却可能不那么简单。理想情况下,仿真的输入数据应反映要建模的实际数量之间已知的相关性。然而,判断仿真中的任何相关性时可以依据的信息可能很少或根本没有,在这种情况下,最好的做法是尝试不同的可能性,以确定模型的敏感性。
但是,当输入数据的分布不是标准多元分布时,很难真正生成具有相关性的随机输入。而且,有些标准多元分布只能对非常有限的几种相关性进行建模。我们可以始终将输入视为各自独立,这很简便,但并不总是合理的,有可能导致错误的结论。
例如,在有关金融风险的蒙特卡罗模拟中,可能有一些表示各种保险损失来源的随机输入。这些输入可以建模为对数正态随机变量。我们会想了解两两输入间的相关性对仿真结果有何影响。确实,从实际数据中可能已经知道,相同的随机条件可对两个损失来源都产生影响,如果在仿真中忽略这一点,可能会导致错误的结论。
独立的对数正态随机变量的仿真非常繁琐。最简单的方法是使用 lognrnd 函数。此处,我们将使用 mvnrnd 函数生成 n 对独立的正态随机变量,然后计算它们的幂。请注意,这里使用的协方差矩阵是对角矩阵,即 Z 的各列之间是独立的。
n = 1000;
sigma = .5;
SigmaInd = sigma.^2 .* [1 0; 0 1]
SigmaInd =
0.2500 0
0 0.2500
ZInd = mvnrnd([0 0], SigmaInd, n);
XInd = exp(ZInd);
plot(XInd(:,1),XInd(:,2),'.');
axis equal;
axis([0 5 0 5]);
xlabel('X1');
ylabel('X2');
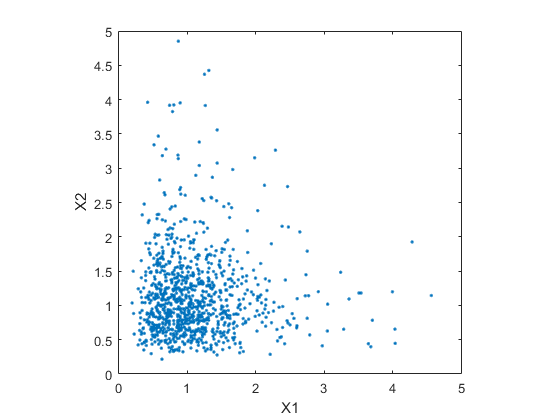
生成具有相关性的二元对数正态随机变量也很简单,可使用非零项不在对角线上的协方差矩阵。
rho = .7;
SigmaDep = sigma.^2 .* [1 rho; rho 1]
SigmaDep =
0.2500 0.1750
0.1750 0.2500
ZDep = mvnrnd([0 0], SigmaDep, n);
XDep = exp(ZDep);
第二个散点图说明这两种二元分布之间的差异。
plot(XDep(:,1),XDep(:,2),'.');
axis equal;
axis([0 5 0 5]);
xlabel('X1');
ylabel('X2');
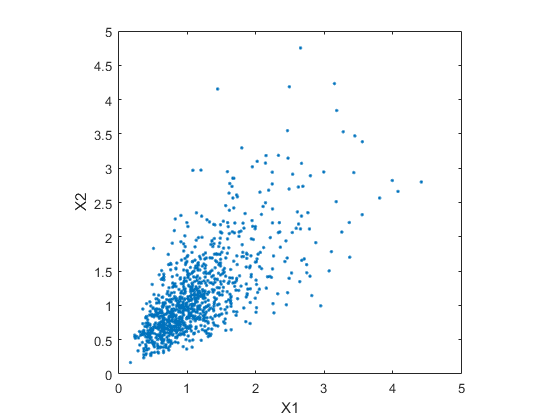
很明显,第二个数据集中较大的 X1 值更倾向于与较大的 X2 值关联,小值之间也是如此。这种相关性由基础二元正态分布的相关参数 rho 决定。从仿真中得出的结论可能很大程度上取决于生成的 X1 和 X2 是否存在相关性。
本示例中的二元对数正态分布是一个简单的解决方法,它当然可以泛化应用于更高维度以及边缘分布为其他对数正态分布的情况。也有一些多元分布,例如,多元 t 分布和 Dirichlet 分布,它们分别用于仿真相关的 t 随机变量和 beta 随机变量。但是,简单的多元分布并不多,而且仅适用于边缘分布都为同一族分布(甚至是完全相同的分布)的情形。在很多情况下,这可能会成为限制。
构造相关二元分布的更通用方法
尽管上面创建二元对数正态分布的构造很简单,但它说明了一种更普遍适用的方法。首先,我们从二元正态分布中生成值对。两两变量间存在统计相关性,而且每个变量都具有正态边缘分布。接下来,分别对每个变量进行变换(指数函数),将边缘分布变成对数正态分布。变换后的变量仍具有统计相关性。
如果能够找到一种合适的变换,就可以将此方法泛化,从而为其他边缘分布生成相关二元随机向量。实际上,确实存在构造这种变换的一般方法,尽管不像求幂那样简单。
根据定义,将正态 CDF(这里用 PHI 表示)应用于标准正态随机变量将生成在区间 [0,1] 内均匀分布的随机变量。为说明这一点,假设 Z 具有标准正态分布,则 U = PHI(Z) 时,CDF 为
Pr{U <= u0} = Pr{PHI(Z) <= u0} = Pr{Z <= PHI^(-1)(u0)} = u0,
而这就是 U(0,1) 随机变量的 CDF。通过为仿真的正态值和仿真的变换值绘制的直方图证实了这一点。
n = 1000;
z = normrnd(0,1,n,1);
hist(z,-3.75:.5:3.75);
xlim([-4 4]);
title('1000 Simulated N(0,1) Random Values');
xlabel('Z');
ylabel('Frequency');

u = normcdf(z);
hist(u,.05:.1:.95)