关注 $Mr.material,$ $更$$多$$精$$彩$！

---

主要专栏内容包括：
$\text{ †《LAMMPS小技巧》：}$ 主要介绍采用分子动力学（$Lammps$）模拟相关安装教程、原理以及模拟小技巧（难度：$★$）
$\text{ ††《LAMMPS实例教程—In文件详解》：}$ 主要介绍采用分子动力学（$Lammps$）模拟相关物理过程模拟。（包含：热导率计算、定压比热容计算，难度：$★$$★$$★$）
$\text{ †††《Lammps编程技巧及后处理程序技巧》：}$ 主要介绍针对分子模拟的动力学过程（轨迹文件）进行后相关的处理分析（需要一定编程能力。难度：$★$$★$$★$$★$$★$）。
$\text{ ††††《分子动力学后处理集成函数—Matlab》：}$ 主要介绍针对后处理过程中指定函数，进行包装，方便使用者直接调用（需要一定编程能力，难度：$★$$★$$★$$★$）。
$\text{ †††††《SCI论文绘图—Python绘图常用模板及技巧》：}$ 主要介绍针对处理后的数据可视化，并提供对应的绘图模板（需要一定编程能力，难度：$★$$★$$★$$★$）。
$\text{ ††††††《分子模拟—Ovito渲染案例教程》：}$ 主要采用 $\mathrm{Ovito}$软件，对 $\mathrm{Lammps}$ 生成的轨迹文件进行渲染（难度：$★$$★$）。

$\text{ 专栏说明（订阅后可浏览对应专栏全部博文）：}$
$注意：$如需只订阅某个单独博文，请联系博主邮箱咨询。$lammps\_materials@163.com$

$♠$$†$ 开源后处理集成程序：请关注专栏《LAMMPS后处理——MATLAB子函数合集整理》
$♠$$†$$†$ 需要付费定制后处理程序请邮件联系：$lammps\_materials@163.com$

---

融化过程中RDF的变化

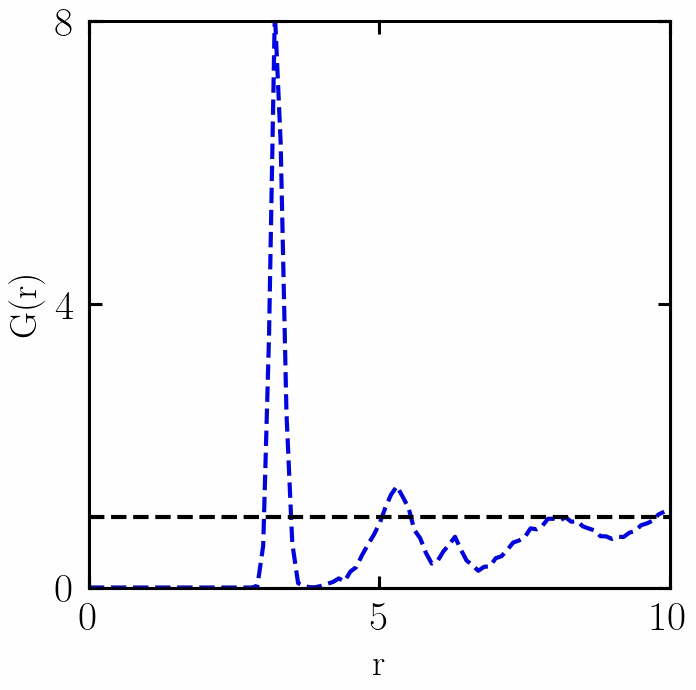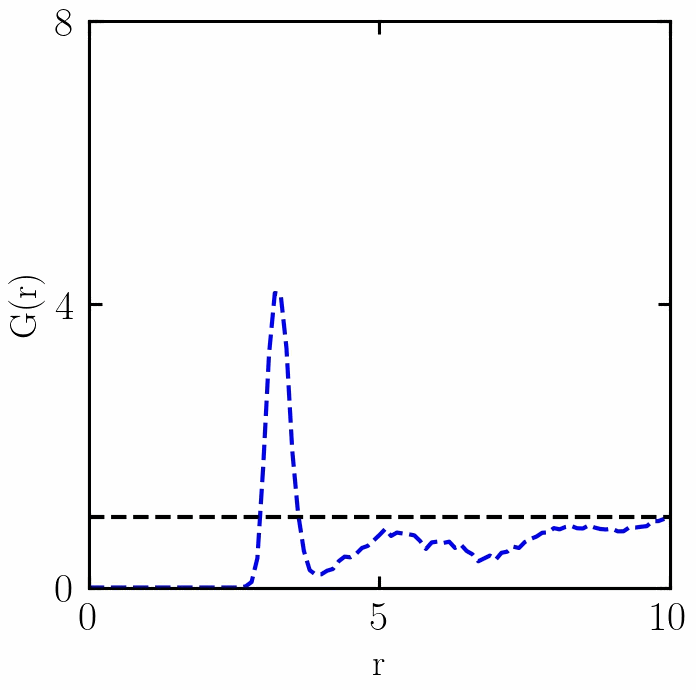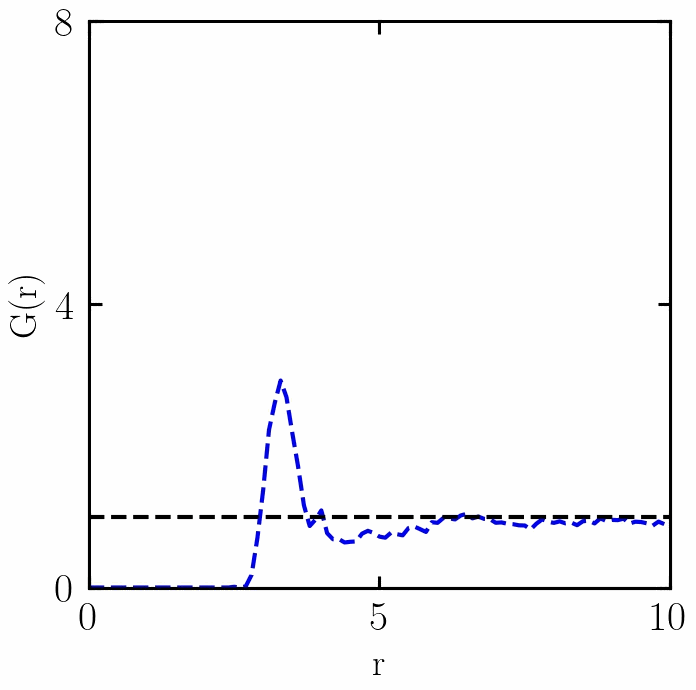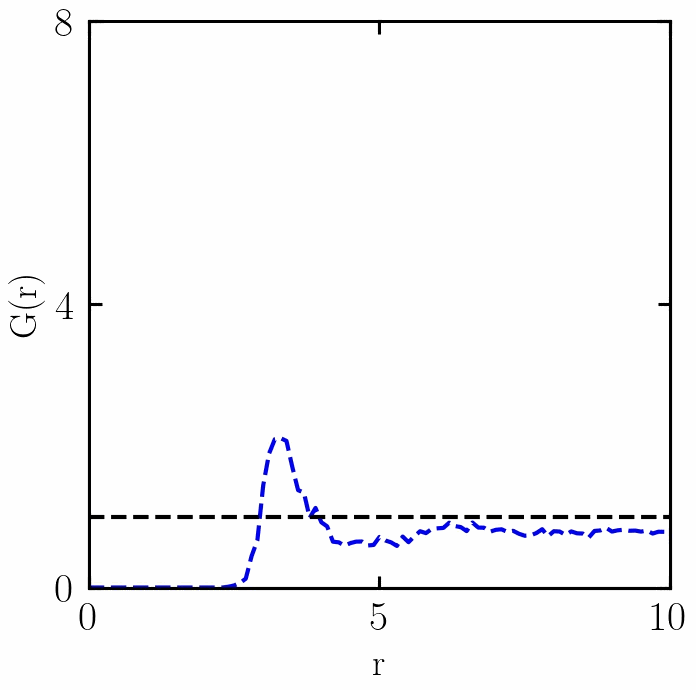
感谢$weixin\_50560116$朋友，提出两个错误：（1）已经更新了PBC函数，（2）t1if 改为 if (复制错误)；

下文翻译自：（请点击）
“结构”意味着粒子的定位是规则的和可预测的。考虑到粒子的短程位置和堆积，这在某种程度上是可能的。局部颗粒密度变化应显示统计平均意义上的某种结构。结构需要一个参考点，在流体的情况下，我们选择单个粒子作为参考，并描述其他粒子相对于该点的位置。由于流体的每个粒子都经历不同的局部环境，因此必须对这些信息进行统计平均，这是我们第一个相关函数的例子。对于大于“相关长度”的距离，我们应该失去预测特定粒子对相对位置的能力。在这个较长的尺度上，流体是均匀的。

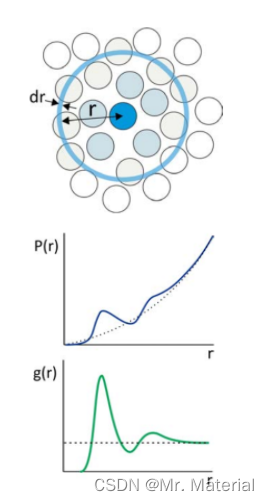
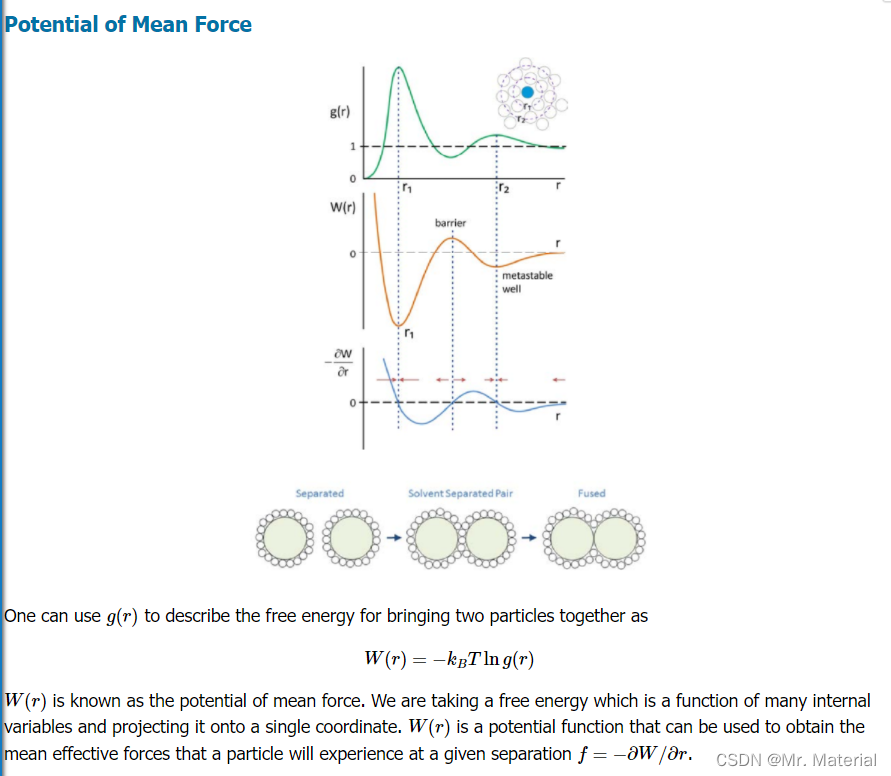
径向分布函数 $g(r)$ 是分子长度尺度上流体“结构”的最有用的度量。尽管它引用了连续统描述，但“流体”指的是任何稠密、无序的系统，其组成粒子的位置存在局部变化，但在宏观上是各向同性的。 $g(r)$ 通过描述中心参考粒子周围粒子的平均分布，提供了系统的局部堆积和粒子密度的统计描述。我们将径向分布函数定义为 $⟨\rho (r)⟩$, 距离r处颗粒的平均局部数密度与颗粒的体积密度 $\rho$ ：

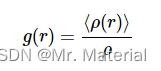
在稠密系统中，$g(r)$ 从零开始（因为它不计算参考粒子），在表征参考粒子周围的第一层粒子（即第一溶剂化层）的距离处上升到峰值，并且在各向同性介质中长距离接近 1。在厚度为dr的壳中距离r处发现粒子的概率为 $P(r)=4\pi r2g(r)dr$，因此对$\rho \cdot g(r)$在中的第一个峰上给出了第一个壳中粒子的平均数量。

径向分布函数最常用于气体、液体和溶液，因为它可以用于计算热力学性质，如系统的内能和压力。但在任何大小的尺度上都是相关的，例如胶体的堆积，并且在复杂的异质介质中是有用的，例如 $DNA$ 周围的离子分布。为了关联不同类型粒子的位置，径向分布函数被定义为距离 $“a”$ 粒子 $r$ 处 $“b”$ 粒子的局部密度之比 $g_{ab}(r)=⟨{\rho }_{ab}(r)⟩/\rho$ 在实践中，${\rho }_{a}b(r)$ 是通过从距离为 $r$ 且厚度为 $dr$ 的壳层上的 $“a”$ 粒子径向观察，计算该壳层内 $“b”$ 粒子的数量，并用该壳层的体积归一化该数量来计算的。

让我们看得更深一点，考虑到相同类型的粒子，如原子液体或颗粒材料中的粒子。如果体积V中有 $N$ 个粒子，且第 $i^{th}$ 个粒子的位置为 $\overline{r_i}$，则数密度描述粒子的位置，

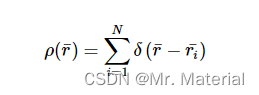
$X(r)$ 给出的径向变化特性的平均值由下式确定：

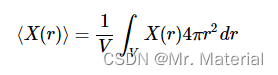
在一个体积上积分 $\overline{\rho (r_i)}$ 可以得到该体积中的粒子数。

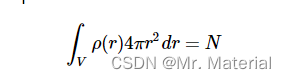
当积分在整个体积上时，我们可以使用它来获得平均粒子密度：

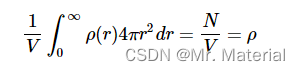
接下来，我们可以考虑两个粒子 $i$ 和 $j$ 之间的空间相关性

这描述了在位置 $r_i$ 处找到粒子 $i$ 和在位置 $r_j$ 处找到粒子 $j$ 的条件概率。根据 $i=j$ 还是 $i$，我们可以将 $\rho (\overline{r},{\vec{r}}^{\prime })$ 展开并因子化为两项$i=j$ or $i$ 不等于 $j$：

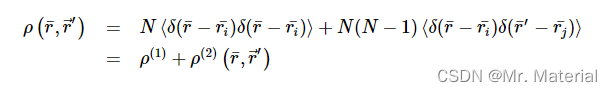
第一项描述了自相关，其中有N项：每个原子一项。

第二项描述了两种身体相关性，其中有N（N‐1）项。

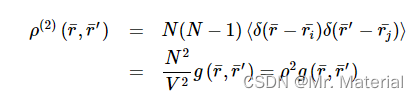
$g()={\rho }^{(2)}(\overline{r},{\vec{r}}^{\prime })/{\rho }^2$ 是双粒子分布函数，描述了两个原子或分子之间的空间相关性。对于各向同性介质，它仅取决于粒子之间的距离，$g(\left|\overline{r},{\vec{r}}^{\prime }\right|)=g(r)$，因此也称为径向对分布函数。

我们可以通过写$g_{ab}(r)$将 $g(r)$ 推广为 $a$ 和 $b$ 粒子的混合物：

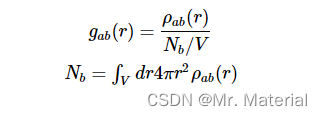
一. 读取dump

读取dump文件，请见博客：
python 读取：https://blog.csdn.net/qq_43689832/article/details/113812304?spm=1001.2014.3001.5502
matlab读取：https://blog.csdn.net/qq_43689832/article/details/108943190?spm=1001.2014.3001.5501
C++ 读取：https://blog.csdn.net/qq_43689832/article/details/104686674

二. 计算RDF

%=========================================================%
bin     = 100;
cutoff  = 5;
%=========================================================%
bin_size = cutoff/bin; calcu_data = atom_data;
all_frame = size(atom_data,3);Gr  = zeros(bin,all_frame);
N   = length(atom_data);vol = xl*yl*zl;
globel_density =N/vol;
%----------------------------------------------------------%for frame = 1:30:all_framenow_frame = calcu_data(:,:,frame);xl = x_bound(1,2)-x_bound(1,1);yl = y_bound(1,2)-y_bound(1,1);zl = z_bound(1,2)-z_bound(1,1);type = now_frame(:,2);XYZ  = now_frame(:,3:5);for ii = 1:Nif(1)for jj = 1:Nif(ii~=jj)dx  = XYZ(jj,1)-XYZ(ii,1);dy  = XYZ(jj,2)-XYZ(ii,2);dz  = XYZ(jj,3)-XYZ(ii,3);PBC(dx,dy,dz,xl,yl,zl);dis = dx^2+dy^2+dz^2;if(sqrt(dis)<cutoff)index = ceil(sqrt(dis)/bin_size);               Gr(index,frame) = Gr(index,frame) + 1;endendendendfor kk = 1:bindV = 4 * pi * (bin_size * kk)^2 * bin_size; Gr(kk,frame) =Gr(kk,frame)./N./dV./globel_density;end
end
%----------------------------------------------------------%
Gr(:,all(Gr == 0,1)) =[];
%----------------------------------------------------------%

%pbc 
function [dx,dy,dz] = PBC(dx,dy,dz,xl,yl,zl)
%-------------------------------------------------%if (dx>xl/2)dx = dx - xl;elseif  (dx<(-xl/2))dx = dx + xl;endif (dy>yl/2)dy = dy - yl;elseif  (dy<(-yl/2))dy = dy + yl;endif (dz>zl/2)dz = dz - zl;elseif  (dz<(-zl/2))dz = dz + zl;end
%-------------------------------------------------%
end

三. 写出文件python画图

import os
def make_save_file(filepath,filename,savename):# filepath 存储路径； filename：创建文件夹的名字 savename：存储图片的名字save_path = filepath+os.sep+filename+os.sep+savenameall_path  = filepath+os.sep+filenameif not os.path.exists(all_path):os.mkdir(all_path)plt.savefig(save_path,dpi=150)
filepath = r"save path"
font1 = {'family': 'Times New Roman','weight': 'bold','size': 22,}
font2 = {'family': 'Times New Roman','weight': 'normal','size': 11,}
# Global setting# ----------------------------------------------------------------------#
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# coding:utf-8
import pylab
import matplotlib.ticker as plticker
from matplotlib.pyplot import MultipleLocator
import xlrd
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import math
def func(x,beita_tar):return 0.022/(1+2*x*beita_tar)plt.style.use('science')
# ----------------------------------------------------------------------#
def setup(ax,x_label,y_label):# 边框线的线宽设置width = 1.5ax.spines['top'].set_linewidth(width)ax.spines['bottom'].set_linewidth(width)ax.spines['left'].set_linewidth(width)ax.spines['right'].set_linewidth(width)# 边框上的ticks的出现ax.tick_params(top='on', bottom='on', left='on', right='on', direction='in')# 边框上的ticks对应的lable,即数字的尺寸ax.tick_params(labelsize=20,pad=7)#ax.yaxis.set_ticks_position('right')ax.tick_params(which='major', width=1.50, length=6)ax.tick_params(which='minor', width=0.75, length=0)# 边框上的ticks的出现的间隔locx = plticker.MultipleLocator(base=5) # this locator puts ticks at regular intervalsax.xaxis.set_major_locator(locx)locy = plticker.MultipleLocator(base=4) # this locator puts ticks at regular intervalsax.yaxis.set_major_locator(locy)# 边框上的注释labelslabels = ax.get_xticklabels() + ax.get_yticklabels()[label.set_fontname('Times New Roman') for label in labels]# 边框上的注释labels距离坐标轴的距离xAxisLable = x_label yAxisLable = y_labelax.set_xlabel(xAxisLable, font1, labelpad=5)ax.set_ylabel(yAxisLable, font1, labelpad=5)
# ----------------------------------------------------------------------#
# 读取excel
excel_path = r"\rdf1.xlsx"
work_sheet = xlrd.open_workbook(excel_path);# sheet的数量
sheet_num = work_sheet.nsheets;
# 获取sheet name
sheet_name = []
for sheet in work_sheet.sheets():sheet_name.append(sheet.name)
# ----------------------------------------------------------------------#
# ----------------------------------------------------------------------#
#fig, axe = plt.subplots(1, 1, figsize=(5,5))
for sheet_num in range(100):# 选取sheetnow_sheet = work_sheet.sheets()[0]#now_sheet_ref = work_sheet.sheets()[3]# sheet的行row = now_sheet.nrows# sheet的列ncol = now_sheet.ncols#----------------------------------------------------------------------##----------------------------------------------------------------------#font1 = {'family': 'Times New Roman','weight': 'bold','size': 18,}font2 = {'family': 'Times New Roman','weight': 'normal','size': 11,}#----------------------------------------------------------------------#     # stepy1        = now_sheet.col_values(sheet_num)y1_matrix = y1[0:]# tempx         = np.arange(100)# stepy2        = now_sheet.col_values(sheet_num)y2_matrix = y2[0:]# press#----------------------------------------------------------------------#markersize = 10  linewidth = 1markevery =1p_1 = dict(marker='o',color = 'r',linestyle = 'none',markersize=markersize,markevery=1, linewidth=linewidth,alpha=0.5)p_2 = dict(color = 'r', linestyle = '-.',linewidth=linewidth)p_3 = dict(color = 'b', linestyle = '--',linewidth=2)p_33 = dict(color = 'r', linestyle = '--',linewidth=2)p_4 = dict(color = 'c', linestyle = '-',linewidth=linewidth)p_5 = dict(color = 'm', linestyle = '-',linewidth=linewidth)p_6 = dict(color = 'y', linestyle = '-',linewidth=linewidth)p_7 = dict(color = 'k', linestyle = '-',linewidth=linewidth)p_8 = dict(color = 'tab:orange',linestyle = '-',linewidth=linewidth)p_9 = dict(color = 'tab:pink',linestyle = '-',linewidth=linewidth)   p_10 = dict(color = 'tab:pink',linestyle = '-',linewidth=linewidth)#----------------------------------------------------------------------#p_fit = dict(color = 'b',linestyle = '--',lw=2)fig, axe = plt.subplots(1, 1, figsize=(5,5))skip=3#axe.scatter(x1_matrix, y1_matrix, **p_s_1,label=legend_1)#x1_fit = np.arange(0.3,1.8,0.01)#y1_fit = 156*exp(-((x1_fit-0.11)/0.94)**2)#y1_fit = 156.9*np.exp(-1.16*(x1_fit-0.11)**2)#axe.plot(x, y1_matrix,**p_2,label='Number density')axe.plot(x*np.array(0.1), y2_matrix,**p_3)#axe.plot(x*np.array(0.1),np.array(y2_matrix).sum(axis=0)/np.array(100),**p_3)plt.axhline(1, color='k', linestyle='--',lw=2)#axe.axvline(x=5000,ymin=-6.5,ymax=-5)#plt.axvline(x=1700,color='k',linestyle='dashed')#axe.plot(np.arange(len(y10_matrix))+1,np.array(y10_matrix)+45,label=legend_10,**p_10)axe.set_ylim(0, 8)axe.set_xlim(0, 10)setup(axe,r'$\rm r$',r'$\rm G(r)$')#axe.legend(loc='best', frameon=False, \#              labelspacing=0.3)#axe.legend(bbox_to_anchor=(1.10, 1), \#              loc='upper left', borderaxespad=0.,fontsize='xx-large')#axe[1].legend(loc='best', frameon=False, labelspacing=0.3)#axe[1].legend(bbox_to_anchor=(1.10, 1), loc='upper left', borderaxespad=0.,fontsize='x-large')# ============================================================#filename = "rdf"savename = str(sheet_num)+'.jpg'make_save_file(filepath,filename,savename)#figureFileName = "Amorphous_overlop.pdf"#print(figureFileName)#plt.savefig(figureFileName, dpi=300)#plt.xscale("log")#plt.yscale("log")# ----------------------------------------------------------------------#plt.show()

全部代码如下

%{
This code is to calculate RDF by LAMMPS dump file
The origin code source is from (see below)
https://github.com/brucefan1983/Molecular-Dynamics-Simulation/tree/master/src/06-properties/rdf
This code is to calculate the each frame from dump file 
%}clc;clear;
%=========================================================%
file ="dump.all";
bin     = 100; % be carefull to select the bin value based on your simulation system
cutoff  = 5;   % 
%=========================================================%
t_start_all = cputime;
trydump = fopen(file,'r');
catcherror('Dumpfile not found!');
endi=1;
while feof(dump) == 0id = fgetl(dump);if (strncmpi(id,'ITEM: TIMESTEP',numel('ITEM: TIMESTEP')))timestep(i) = str2num(fgetl(dump));elseif (strncmpi(id,'ITEM: NUMBER OF ATOMS',numel('ITEM: NUMBER OF ATOMS')))Natoms(i) = str2num(fgetl(dump));elseif (strncmpi(id,'ITEM: BOX BOUNDS',numel('ITEM: BOX BOUNDS')))x_bound(i,:) = str2num(fgetl(dump));y_bound(i,:) = str2num(fgetl(dump));z_bound(i,:) = str2num(fgetl(dump));elseif (strcmpi(id(1:11),'ITEM: ATOMS'))for j = 1 : 1: Natomsatom_data(j,:,i) = str2num(fgetl(dump));endi=i+1;endend endend
end
t_start_stop = (cputime-t_start_all)/60;
fprintf('Now the used time is: %.1f mins.\n',t_start_stop);
disp("-------------------");
disp("----ALL DONE!!!----");
disp("-------------------");
% 这个是自动关机-
% system('shutdown -s');
bin_size = cutoff/bin; calcu_data = atom_data;
all_frame = size(atom_data,3);Gr  = zeros(bin,all_frame);
N   = length(atom_data);vol = xl*yl*zl;
globel_density =N/vol;
%----------------------------------------------------------%for frame = 1:30:all_framenow_frame = calcu_data(:,:,frame);xl = x_bound(1,2)-x_bound(1,1);yl = y_bound(1,2)-y_bound(1,1);zl = z_bound(1,2)-z_bound(1,1);type = now_frame(:,2);XYZ  = now_frame(:,3:5);for ii = 1:Nif(1)for jj = 1:Nif(ii~=jj)dx  = XYZ(jj,1)-XYZ(ii,1);dy  = XYZ(jj,2)-XYZ(ii,2);dz  = XYZ(jj,3)-XYZ(ii,3);PBC(dx,dy,dz,xl,yl,zl);dis = dx^2+dy^2+dz^2;t1if(sqrt(dis)<cutoff)index = ceil(sqrt(dis)/bin_size);               Gr(index,frame) = Gr(index,frame) + 1;endendendendfor kk = 1:bindV = 4 * pi * (bin_size * kk)^2 * bin_size; Gr(kk,frame) =Gr(kk,frame)./N./dV./globel_density;end
end
%----------------------------------------------------------%
Gr(:,all(Gr == 0,1)) =[];
%----------------------------------------------------------%