假设有两个高斯分布：
p 1 ( x ) = ( 2 π σ 1 2 ) − 1 2 e x p { − 1 2 ( x − μ 1 ) 2 σ 1 2 } p_1(x) = (2\pi\sigma_1^2)^{-\frac{1}{2}}exp\{ -\frac{1}{2} \frac{(x-\mu_1)^2}{\sigma_1^2} \} p1​(x)=(2πσ12​)−21​exp{−21​σ12​(x−μ1​)2​} p 2 ( x ) = ( 2 π σ 2 2 ) − 1 2 e x p { − 1 2 ( x − μ 2 ) 2 σ 2 2 } p_2(x) = (2\pi\sigma_2^2)^{-\frac{1}{2}}exp\{ -\frac{1}{2} \frac{(x-\mu_2)^2}{\sigma_2^2}\} p2​(x)=(2πσ22​)−21​exp{−21​σ22​(x−μ2​)2​}

高斯分布相乘

计算这两个高斯分布的乘积:
p 1 ( x ) p 2 ( x ) = 1 2 π σ 1 2 σ 2 2 e x p { − { ( x − μ 1 ) 2 2 σ 1 2 + ( x − μ 2 ) 2 2 σ 2 2 } } p_1(x)p_2(x) = \frac{1}{2\pi \sqrt{\sigma_1^2\sigma_2^2} }exp\{ -\{ \frac{(x-\mu_1)^2}{2\sigma_1^2} + \frac{(x-\mu_2)^2}{2\sigma_2^2} \} \} p1​(x)p2​(x)=2πσ12​σ22​ ​1​exp{−{2σ12​(x−μ1​)2​+2σ22​(x−μ2​)2​}}
高斯分布的乘积还是高斯分布，且根据这篇博客直观理解高斯相乘可以计算出$p_1(x)p_2(x)$的均值$\mu$和方差$\sigma$。
$$\mu =\frac{{\mu }_1{\sigma }_2^2+{\mu }_2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}$$ $$\frac{1}{{\sigma }^2}=\frac{1}{{\sigma }_1^2}+\frac{1}{{\sigma }_2^2}$$ $${\sigma }^2=\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}$$
接下来分析一下$\mu$和${\sigma }^2$
首先是均值$\mu$
$$\mu -{\mu }_1=\frac{{\mu }_1{\sigma }_2^2+{\mu }_2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}-\frac{{\mu }_1{\sigma }_1^2+{\mu }_1{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}=\frac{({\mu }_2-{\mu }_1){\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}$$ $$\mu -{\mu }_2=\frac{{\mu }_1{\sigma }_2^2+{\mu }_2{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}-\frac{{\mu }_2{\sigma }_1^2+{\mu }_2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}=\frac{({\mu }_1-{\mu }_2){\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}$$
当${\mu }_1>{\mu }_2$时：
$\mu -{\mu }_1<0,\mu -{\mu }_2>0$ 所以，${\mu }_2<\mu <{\mu }_1$
当${\mu }_1<{\mu }_2$时：
$\mu -{\mu }_1>0,\mu -{\mu }_2<0$ 所以，${\mu }_1<\mu <{\mu }_2$
当${\mu }_1={\mu }_2$时：
$\mu -{\mu }_1=0,\mu -{\mu }_2=0$ 所以，${\mu }_1=\mu ={\mu }_2$
可以看出$\mu$是位于${\mu }_1$和${\mu }_2$之间。

接下来是方差$\sigma$
$${\sigma }^2-{\sigma }_1^2=\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}-{\sigma }_1^2=\frac{-{\sigma }_1^4}{{\sigma }_1^2+{\sigma }_2^2}<0$$ $${\sigma }^2-{\sigma }_2^2=\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}-{\sigma }_2^2=\frac{-{\sigma }_2^4}{{\sigma }_1^2+{\sigma }_2^2}<0$$
所以$p_1(x)p_2(x)$的方差比$p_1(x)$和$p_2(x)$的方差都要小。

代码验证高斯分布相乘

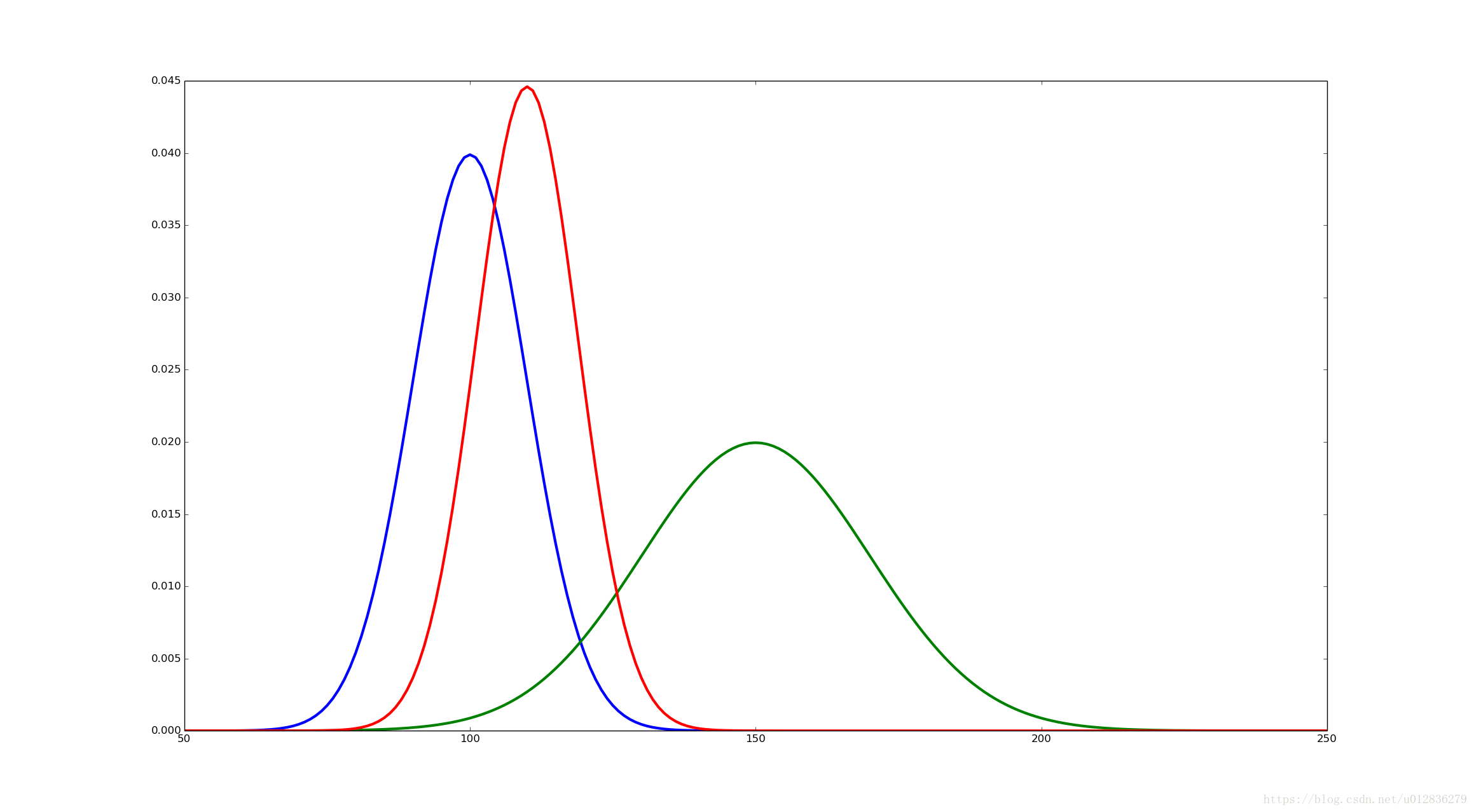
紧接着，通过python代码验证这个结果：
其中，红色的曲线表示高斯分布的乘积，其详细的代码如下所示：

import matplotlib.pyplot as plt
from math import *class Distribution:def __init__(self,mu,sigma,x,values,start,end):self.mu = muself.sigma = sigmaself.values = valuesself.x = xself.start = startself.end =enddef normalize(self):s = float(sum(self.values))if s != 0.0:self.values = [i/s for i in self.values]def value(self, index):index -= self.startif index<0 or index >= len(self.values):return 0.0else:return self.values[index]@staticmethoddef gaussian(mu,sigma,cut = 5.0):sigma2 = sigma*sigmaextent = int(ceil(cut*sigma))values = []x_lim=[]for x in xrange(mu-extent,mu+extent+1):x_lim.append(x)values.append(exp((-0.5*(x-mu)*(x-mu))/sigma2))p1=Distribution(mu,sigma,x_lim,values,mu-extent,mu-extent+len(values))p1.normalize()return p1if __name__=='__main__':p1 = Distribution.gaussian(100,10)plt.plot(p1.x,p1.values,"b-",linewidth=3)p2 = Distribution.gaussian(150,20)plt.plot(p2.x,p2.values,"g-",linewidth=3)start = min(p1.start,p2.start)end = max(p1.end,p2.end)mul_dist = []x_lim = []for index in range(start,end):x_lim.append(index)mul_dist.append(p1.value(index)*p2.value(index))#normalize the distributions= float(sum(mul_dist))if s!=0.0:mul_dist=[i/s for i in mul_dist]plt.plot(x_lim,mul_dist,"r-",linewidth=3)plt.show()