由于篇幅有限,前一篇文章《离散分布的产生》中只讲述了用均匀分布产生离散分布的方法,那么本文接着讲如何利用均匀分布产生连续分布的方法。
连续分布
连续分布主要有以下几种:均匀分布 伽马分布 正态分布 贝塔分布 柯西分布 对数正态分布 双指数分布。
产生各种连续分布的方法有很多,我把它分为两类:通用方法、特殊方法。特殊方法就是根据各个连续分布的特性而特有的方法。
通用方法
通用方法指的是对于各种连续分布理论上都适用的方法。下面只讲解分布函数法、舍取法这两种通用的方法。
分布函数法
概率积分变换定理
设随机变量 X 有连续累计分布函数
由概率积分变换定理可知,如果知道一个连续分布函数的累计分布函数 F(x) ,则可以求得随机变量: X=F−1(U) ,其中 U 服从
指数分布的累计分布函数 F(x) 可以表示为:
由于 U=F(X) 服从 (0,1) 上的均匀分布,则随机变量: X=F−1(U)=−Ln(1−U)λ 。因此只需要产生服从 (0,1) 上的均匀分布的 U ,就可以计算得到服从指数分布的随机变量X。
- 指数分布
%指数分布
%参数:到达率lambda
%mean=1/lamda, var=1/lambda^2
clear all
close all
clc
lambda=1;%指数分布的产生lambda
n=10;%x的取值为0到无穷大,这里只取前n个%------------------------由内置函数直接给出-------------------------%%指数分布的产生,即事件发生的时间间隔x,x取值为0到正无穷
X=exprnd(1/lambda);%产生1均值为1/lamda的指数分布%指数分布的cdf
x=0:.1:n;
Fx=expcdf(x,1/lambda);
%figure
%plot(x,Fx,'-')
%title('指数分布的cdf')%指数分布的pdf
x=0:.1:n;
Px=exppdf(x,1/lambda);
figure
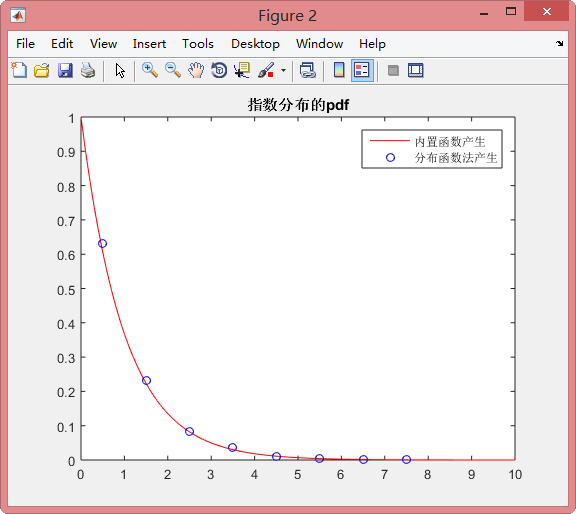
plot(x,Px,'r-')
hold on
title('指数分布的pdf')%-------------------------由均匀分布推导出(分布函数法)-------------------------%
N=1000;%样本点数
U=rand(1,N);%U服从均匀分布X2=-(log(1-U))/lambda;%X2服从指数分布,X2由分布函数法得到,对于不同的分布,分布函数不同,这里的表达式需作相应的改变!%下面的程序是绘制X2的概率密度函数pdf
Max=ceil(max(X2));
step=1;%步长
range=0:step:Max;for i=1:length(range)-1YY(i)=sum(range(i)<=X2&X2<=range(i+1))/N/step;%统计落在区间中的点数XX(i)=(range(i)+range(i+1))/2;
endplot(XX,YY,'bo')
hold on
title('指数分布的pdf')
legend('内置函数产生','分布函数法产生')结果显示如下:(指数参数
分布函数法的局限性:由于该方法的关键就是求出分布函数的反函数,从而得到随机变量 X 关于均匀分布随机变量
其中, u 和
舍去法
定理:设随机变量 下面以用舍去法生成正态分布来具体说明:假设我们要用舍取法生成标准正态分布,标准正态分布的概率密度函数如下所示: 确定 V 的分布 确定 在确定了 V 的分布以及 结果显示如下: 注意:使用这种方法的时候必须使 上述的两种通用方法基本上可以用均匀分布产生大多数连续分布,不过由于每种分布有着各自的特性,因此也可以通过特殊的方法来生成。下面以生成标准正态分布(正态分布性质表明:任何正态分布都可以由标准正态分布转化得到)为例: 中心极限定理是概率论中的一组定理。中心极限定理说明,大量相互独立的随机变量,其均值的分布以正态分布为极限。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量之和近似服从正态分布的条件。(摘自维基百科) 在程序实现中,我利用 10 个相互独立的服从区间 −5到5 的均匀分布来生成标准正态分布 Y 。而由公式可知,区间 显示结果如下: 基本思想:假设 U,V 是两个相互独立的且服从区间在 0到1 的均匀分布,并且随机变量 X,Y 的表达式如下: 具体的程序实现如下: 显示结果如下: 上面我们是以正态分布为例来讲述了特殊法的运用,主要是运用了正态分布与其他分布的关系:多个独立同分布的随机变量和服从正态分布;均匀分布与正态分布之间满足Box-Muller法中的关系。因此,当想要由一种分布生成另一种分布的时候,只需要知道它们之间的关系即可! 原文:http://blog.csdn.net/tengweitw/article/details/45599011 作者:nineheadedbird
按下列步骤可以生成随机变量
Y 服从概率密度为
1. 生成独立的随机变量
U,V ,其中,
U 服从
2. 如果
U<1MfY(V)/fV(V) ,则令
Y=V ,否则返回到步骤1。
由舍取法的步骤2可知,生成的正态分布变量
理论上,正态随机变量的取值在整个实数域中,因此
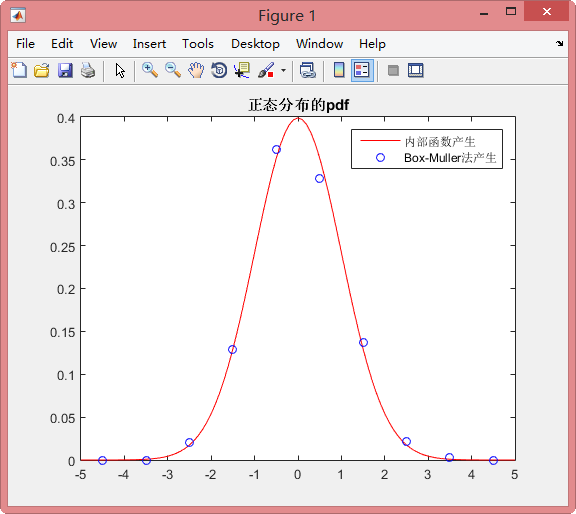
在公式 M=max{fY(y)/fV(v)} 中, fV(v)=110 , max{fY(y)}=fY(0)=12π√ 。因此 M=102π√ %-------------------正态分布-----------------------%
%参数:均值mu,方差sigma2
%mean=mu, var=sigma2
clear all
close all
clc
mu=0;
sigma2=1;
n=10;%x的取值为正负无穷大,
%-------------------由内置函数直接给出----------------%
%正态分布的产生X
X=normrnd(mu,sqrt(sigma2));%产生均值mu,方差sigma2的正态分布%正态分布的cdf
x=0:.1:n;
Fx=normcdf(x,mu,sqrt(sigma2));
% figure
% plot(x,Fx,'-')
% title('正态分布的cdf')%指数分布的pdf
x=-5:.1:5;
Px=normpdf(x,mu,sqrt(sigma2));
figure
plot(x,Px,'b-')
hold on%------由舍选法推导出--------%N=100;
A=-5;%A,B位均匀分布的取值区间
B=5;i=1;
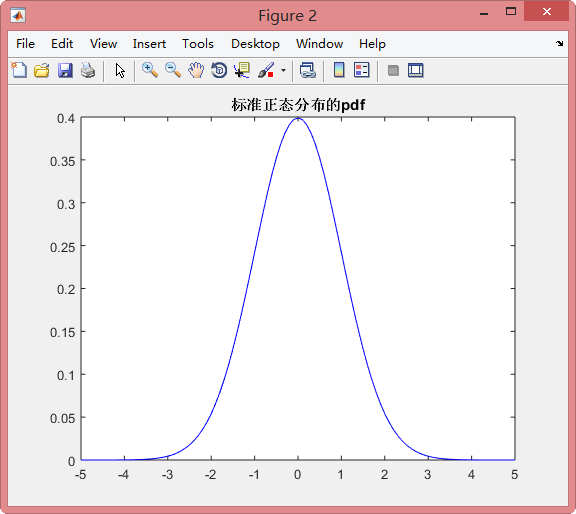
while(i<=N)U=unifrnd(0,1);%服从(0,1)的均匀分布V=unifrnd(A,B);%服从(A,B)的均匀分布M=1/sqrt(2*pi)*(B-A);%计算得到Mif(U<1/M*1/sqrt(2*pi*sigma2)*exp(-(V-mu)^2/2/sigma2));%由定理得到的公式来生成随机变量X2X2(i)=V;%X2就是我们要生成的指定分布的随机变量i=i+1;end
end%下面的程序是计算通过舍去法生成的正态分布X2的pdf
Max=ceil(max(X2));
step=1;
range=A:step:B;for i=1:length(range)-1YY(i)=sum(range(i)<=X2&X2<=range(i+1))/N/step;XX(i)=(range(i)+range(i+1))/2;
endplot(XX,YY,'ro')
hold on
title('正态分布的pdf')
legend('内部函数产生','舍取法产生')
特殊方法
中心极限定理法
我们由中心极限定理可知,多个独立同分布的随机变量的和服从正态分布,而关于这个正态分布的均值和方差的确定,我们可以依据林德伯格-列维定理:
林德伯格-列维(Lindeberg-Levy)定理:
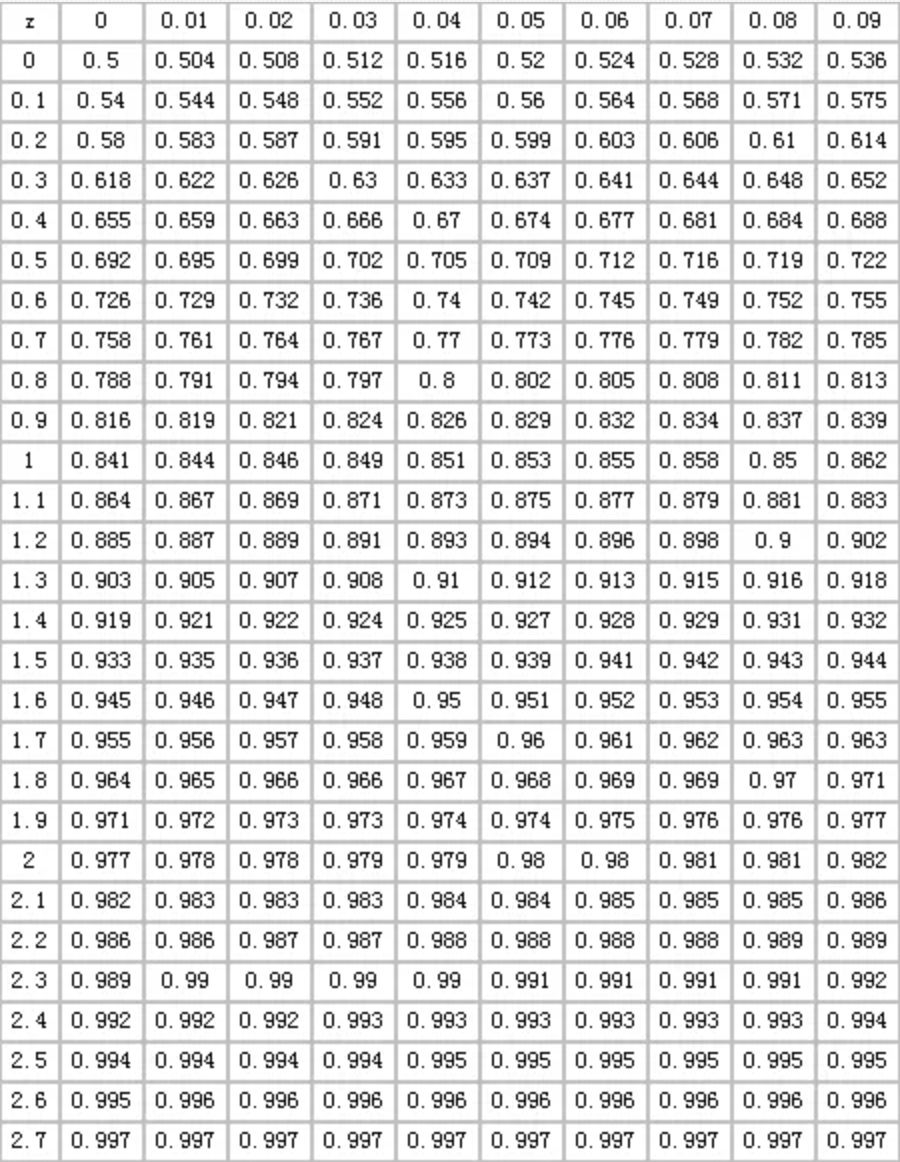
设随机变量 X1,X2,⋯,Xn ,且具有有限的数学期望 E(Xi)=u,D(Xi)=σ2=0(i=1,2,⋯,n) 。记 X¯=1n∑i=1nXi,Y=X¯−uσ/n√ ,则 limn→∞P(Y<z)=Φ(z) ,其中 Φ(z) 是标准正态分布的分布函数。%-------------------正态分布-----------------------%
%参数:均值mu,方差sigma2
%mean=mu, var=sigma2
clear all
close all
clc
mu=0;
sigma2=1;
n=10;%x的取值为正负无穷大,
%------------------由内置函数直接给出--------------%
%正态分布的产生X
X=normrnd(mu,sqrt(sigma2));%产生均值mu,方差sigma2的正态分布%正态分布的cdf
x=0:.1:n;
Fx=normcdf(x,mu,sqrt(sigma2));
% figure
% plot(x,Fx,'-')
% title('正态分布的cdf')%指数分布的pdf
x=-5:.1:5;
Px=normpdf(x,mu,sqrt(sigma2));
figure
plot(x,Px,'b-')
hold on
%-------------------由中心极限定理推导出---------------------%
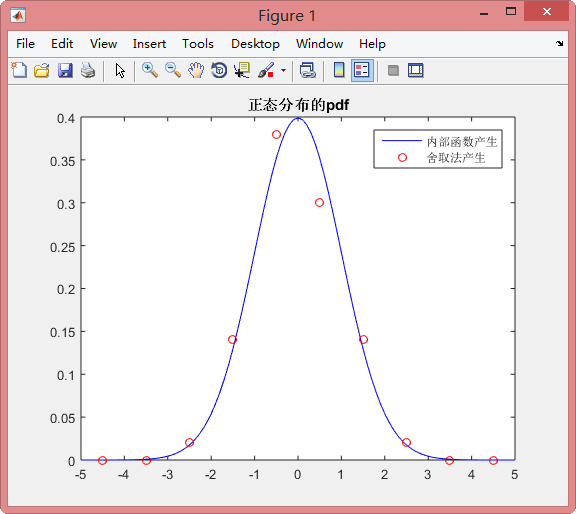
N=1000;%样本点数
A=-5;%A,B位均匀分布的取值区间
B=5;for i=1:10
U(i,1:N)=unifrnd(A,B,1,N);%U存储10个独立的服从均匀分布的随机变量
end
meanX=mean(U);
X2=(meanX-(A+B)/2)/sqrt((B-A)^2/12)*sqrt(10);%由林德伯格-列维定理的公式知X2服从正态分布
mean(X2);%下面的程序是计算通过中心极限定理法生成的正态分布X2的pdf
Max=ceil(max(X2));
step=1;
range=A:step:B;for i=1:length(range)-1YY(i)=sum(range(i)<=X2&X2<=range(i+1))/N/step;XX(i)=(range(i)+range(i+1))/2;
endplot(XX,YY,'ro')
hold on
title('正态分布的pdf')
legend('内部函数产生','中心极限定理法产生')
Box-Muller法
则 X,Y 是相互独立的,并且服从标准正态分布。 %-------------------正态分布-----------------------%
%参数:均值mu,方差sigma2
%mean=mu, var=sigma2
clear all
close all
clc
mu=0;
sigma2=1;
n=10;%x的取值为正负无穷大,
%--------------------由内置函数直接给出----------------------%
%正态分布的产生X
X=normrnd(mu,sqrt(sigma2));%产生均值mu,方差sigma2的正态分布%正态分布的cdf
x=0:.1:n;
Fx=normcdf(x,mu,sqrt(sigma2));
% figure
% plot(x,Fx,'-')
% title('正态分布的cdf')%指数分布的pdf
x=-5:.1:5;
Px=normpdf(x,mu,sqrt(sigma2));
figure
plot(x,Px,'r-')
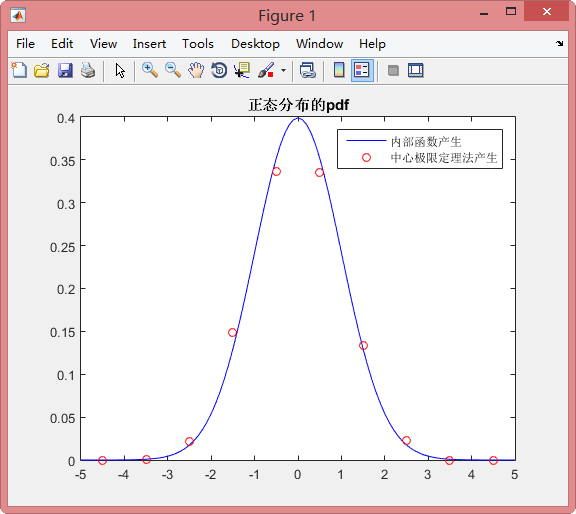
hold on%-----------------------Box-Muller法-----------------------%
N=1000;
U=rand(1,N);%U,V都是服从(0,1)的均匀分布
V=rand(1,N);
A=-5;
B=5;
R=sqrt(-2.*log(U));
theta=2*pi*V;X2=R.*cos(theta);
Y2=R.*sin(theta);%X,Y都是服从n(0,1)的正态分布%下面的程序是计算通过Box-Muller法生成的正态分布X的pdf
Max=ceil(max(X2));
step=1;
range=A:step:B;for i=1:length(range)-1YY(i)=sum(range(i)<=X2&X2<=range(i+1))/N/step;XX(i)=(range(i)+range(i+1))/2;
endplot(XX,YY,'bo')
hold on
title('正态分布的pdf')
legend('内部函数产生','Box-Muller法产生')