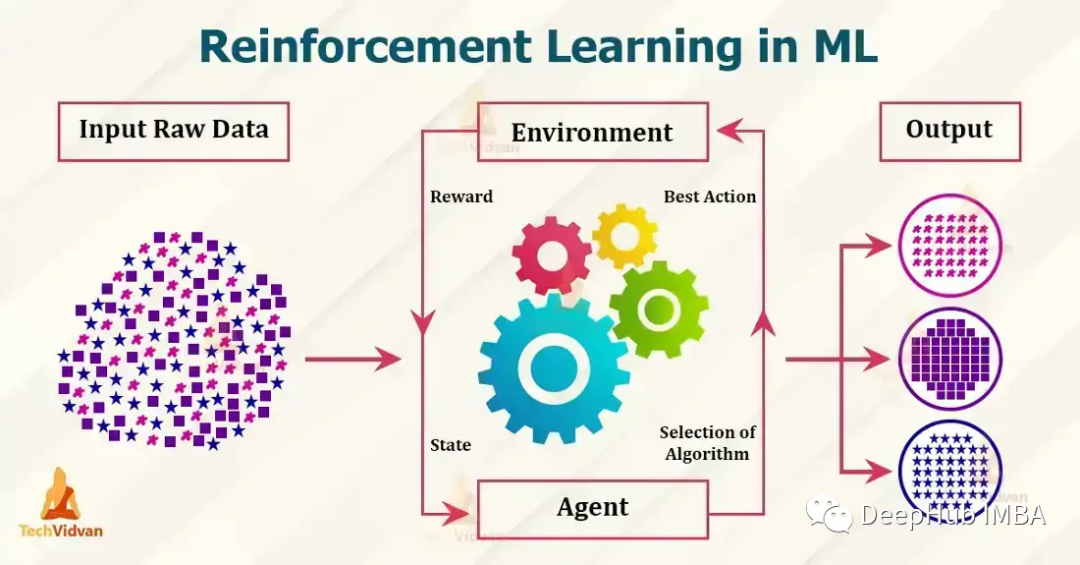
一、前言

局部线性嵌入（LLE）假设数据在较小的局部是线性的，也就是说，某一个样本可以由它最近邻的几个样本线性表示，离样本远的样本对局部的线性关系没有影响，因此相比等距映射算法，降维的时间复杂度和空间复杂度都有极大的降低。
比如有一个样本$x_1$ ，我们在它的原始高维邻域里用$K$-近邻思想找到和它最近的三个样本$x_2,x_3,x_4$，然后我们假设$x_1$可以由$x_2,x_3,x_4$线性表示，即：
$$x_1=w_{12}{x}_2+w_{13}{x}_3+w_{14}{x}_4$$

其中，$w_{12},w_{13},w_{14}$为权重系数。
在我们通过LLE降维后，我们希望$x_1$在低维空间对应的投影$y_1$ 和 $x_2,x_3,x_4$对应的投影$y_2,y_3,y_4$也尽量保持同样的线性关系（局部数据结构不变），即:
$$y_1\approx w_{12}{y}_2+w_{13}{y}_3+w_{14}{y}_4$$

也就是说，投影前后线性关系的权重系数$w_{12},w_{13},w_{14}$是尽量不变或者最小改变的。
因为LLE是基于局部的，所以K近邻的选取是至关重要的。

二、主要步骤

2.1 首先要确定邻域大小

假设这个值为k。我们可以通过和$KNN$一样的思想通过距离度量比如欧式距离来选择某样本的$k$个最近邻。

2.2 确定目标损失函数

在找到某个样本的$x_i$的$k$个最近邻之后，我们就需要找到找到$x_i$和这$k$个最近邻之间的线性关系，也就是要找到线性关系的权重系数。
假设我们有$m$个$n$维样本$x_1,x_2,\cdots ,x_m$，我们可以用均方差作为问题的损失函数：即：
$$J(w)=\sum _{i=1}^m||x_i-\sum _{j=1}^k{w}_{ij}{x}_j|{|}_2^2$$
对权重系数$w_{ij}$做归一化的约束，即权重系数需要满足:
$$\sum _{j=1}^k{w}_{ij}=1$$

通过上面两个式子求出我们的权重系数。

2.3 目标函数优化

对于目标损失函数，将其矩阵化，进行以下推导：
$$\begin{array}{rl}& J(w)=\sum _{i=1}^m||x_i-\sum _{j=1}^k{w}_{ij}{x}_j|{|}_2^2\\ & =\sum _{i=1}^m||\sum _{j=1}^k{w}_{ij}{x}_i-\sum _{j=1}^k{w}_{ij}{x}_j|{|}_2^2\\ & =\sum _{i=1}^m||\sum _{j=1}^k{w}_{ij}(x_i-x_j)|{|}_2^2\\ & =\sum _{i=1}^m{W}_i^T{X}_i{X}_i^{T}Wi\\ & =\sum _{i=1}^m{W}_i^T{Z}_i{W}_i\end{array}$$
其中$W_i=(w_{i1},w_{i2},\cdots ,w_{ik}{)}^T$，$X_i=(x_i-x_1,x_i-x_2,\cdots ,x_i-x_k{)}^T$，$Z_i=X_i{X}_i^T$，
约束条件可化为${\sum }_{j=1}^k{w}_{ij}=W_i{1}_k=1$，
其中$1_k$为$k$维全为1的向量。

2.4 拉格朗日乘子法求解

构造拉格朗日函数：
$$L(W)=\sum _{i=1}^m{W}_i^T{Z}_i{W}_i+\lambda (W_i{1}_k-1)$$

对$W$求导并令其值为0，我们得到:
$$\frac{\partial L(W)}{\partial W}=2Z_i{W}_i+\lambda 1_k=0$$

即我们的
$$W_i={\lambda }^{\prime }{Z}_i^{-1}{1}_k$$
其中 ${\lambda }^{\prime }=-\frac{1}{2}\lambda$为一个常数。那么最终我们的权重系数Wi为：
$$W_i=\frac{Z_i^{-1}{1}_k}{1_k^T{Z}_i^{-1}{1}_k}$$
现在我们得到了高维的权重系数，那么我们希望这些权重系数对应的线性关系在降维后的低维一样得到保持。
假设我们的n维样本集$x_1,x_2,...,x_m$在低维的d维对应投影为$y_1,y_2,...,y_m$，则我们希望保持线性关系，也就是希望对应的均方差损失函数最小，即最小化损失函数$J(Y)$如下：
$$\begin{gathered} J(y)=\sum _{i=1}^m||y_i-\sum _{j=1}^m{w}_{ij}{y}_j|{|}_2^2 \\ =\sum _{i=1}^m||Y{I}_i-Y{W}_i|{|}_2^2 \\ =Tr(Y(I-W)(I-W{)}^T{Y}^T) \\ =Tr(Y^{T}MY) \end{gathered}$$
其中，$M=(I-W{)}^T(I-W)$，上式约束条件为：${\sum }_{i=1}^m{y}_i=0;\frac{1}{m}{\sum }_{i=1}^m{y}_i{y}_i^T=I，即Y^{T}Y=mI$。
接下来利用拉格朗日乘子法对以上式子进行求解：
$$L(Y)=Tr(Y^{T}MY)+\lambda (Y^{T}Y-mI)$$

与拉普拉斯特征映射相似（Laplacian Eigenmaps），最后要得到最小的d维数据集，我们需要求出矩阵$M$最小的d个非0特征值所对应的特征向量组成的矩阵$Y=(y_1,y_2,\cdots ,y_d)$即可。

三、算法流程总结

现在我们对算法过程做一个总结。整个LLE算法用一张图可以表示如下：

从图中可以看出，LLE算法主要分为三步，
第一步是求$K$近邻的过程，这个过程使用了和$KNN$算法一样的求最近邻的方法。
第二步，就是对每个样本求它在邻域里的$K$个近邻的线性关系，得到线性关系权重系数$W$。
第三步就是利用权重系数 来在低维里重构样本数据.

具体过程如下：

• 输入：样本集$D=x_1,x_2,...,x_m$，最近邻数k，降维到的维数d
• 输出：低维样本集矩阵$D^{\prime }$

1. $i=1\to m$， 按欧式距离作为度量，计算$m$个样本点$x_i$最近的的$k$个最近邻$(x_{i1},x_{i2},...,x_{ik})$
2. $i=1\to m$，求出局部协方差矩阵$Z_i=(x_i-x_j)(x_i-x_j{)}^T$，求出对应的权重系数向量:$W_i=\frac{Z_i^{-1}{1}_k}{1_k^T{Z}_i^{-1}{1}_k}$。
3. 由权重系数向量$W_i$组成权重系数矩阵$W$,计算矩阵$M=(I-W)(I-W{)}^T$
4. 由第2个特征向量到第d+1个特征向量所张成的矩阵即为输出低维样本集矩阵$D^{\prime }=(y_2,y_3,...y_{d+1})$

四、改进算法

LLE算法很简单高效，但是却有一些问题，比如如果近邻数k大于输入数据的维度时，我们的权重系数矩阵不是满秩的。为了解决这样类似的问题，有一些LLE的变种产生出来。比如：Modified Locally Linear Embedding(MLLE) 和 Hessian Based LLE(HLLE)。

对于HLLE，它不是考虑保持局部的线性关系，而是保持局部的Hessian矩阵的二次型的关系。而对于MLLE，它对搜索到的最近邻的权重进行了度量，我们一般都是找距离最近的k个最近邻就可以了，而MLLE在找距离最近的k个最近邻的同时要考虑近邻的分布权重，它希望找到的近邻的分布权重尽量在样本的各个方向，而不是集中在一侧。

另一个比较好的LLE的变种是Local tangent space alignment(LTSA)，它希望保持数据集局部的几何关系，在降维后希望局部的几何关系得以保持，同时利用了局部几何到整体性质过渡的技巧。

这些算法原理都是基于LLE，基本都是在LLE这三步过程中寻求优化的方法。

LLE总结

LLE是广泛使用的图形图像降维方法，它实现简单，但是对数据的流形分布特征有严格的要求。比如不能是闭合流形，不能是稀疏的数据集，不能是分布不均匀的数据集等等，这限制了它的应用。下面总结下LLE算法的优缺点。

LLE算法的主要优点有：

1）可以学习任意维的局部线性的低维流形

2）算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易。

LLE算法的主要缺点有：

1）算法所学习的流形只能是不闭合的，且样本集是稠密均匀的。

2）算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。

参考博文连接：https://www.cnblogs.com/pinard/p/6266408.html