转载自:https://blog.csdn.net/sinat_32043495/article/details/78997758
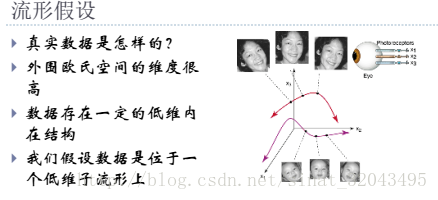
嵌入在高维空间的低维流形
流形:局部具有欧几里得空间性质的空间
1.较好的描述转载
作者:暮暮迷了路
链接:https://www.zhihu.com/question/24015486/answer/194284643
来源:知乎
流形学习的观点是认为,我们所能观察到的数据实际上是由一个低维流形映射到高维空间上的。由于数据内部特征的限制,一些高维中的数据会产生维度上的冗余,实际上只需要比较低的维度就能唯一地表示。
举个例子,比如说我们在平面上有个圆,如何表示这个圆呢?如果我们把圆放在一个平面直角坐标系中,那一个圆实际上就是由一堆二维点构成的。
比如一个单位圆:(1,0) 是一个在圆上的点, (0,1) 也是一个在圆上的点,但(0.0) 和(2,3) 等等很多点是不在这个圆上的。显然如果用二维坐标来表示,我们没有办法让这个二维坐标系的所有点都是这个圆上的点。也就是说,用二维坐标来表示这个圆其实是有冗余的。我们希望,如果能建立某一种描述方法,让这个描述方法所确定的所有点的集合都能在圆上,甚至能连续不间断地表示圆上的点,那就好了!有没有这种方法呢?对于圆来说,当然有!那就是用极坐标。在极坐标的表示方法下,圆心在原点的圆,只需要一个参数就能确定:半径。当你连续改变半径的大小,就能产生连续不断的“能被转换成二维坐标表示”的圆。所以说,实际上二维空间中的圆就是一个一维流形。
与之相似的,三维空间中一个球面,用x, y, z三个坐标轴确定时会产生冗余(很多在三维空间中的数据点并不在球面上)。但其实只需要用两个坐标就可以确定了,比如经度和维度。
只要给定任何合法的精度和维度,我们就都能保证这个点肯定在球面上!
那么,流形学习有什么用呢?我现在能想到的主要有两个方面。
先说第一个方面。高维空间有冗余,低维空间没冗余。也就是说,流形可以作为一种数据降维的方式。传统很多降维算法都是用欧氏距离作为评价两个点之间的距离函数的。但是仔细想想这种欧氏距离直觉上并不靠谱。“我们只是看到了三维数据,就要用三维坐标系内的尺度去对事物进行评价?”总觉得有些怪怪的。
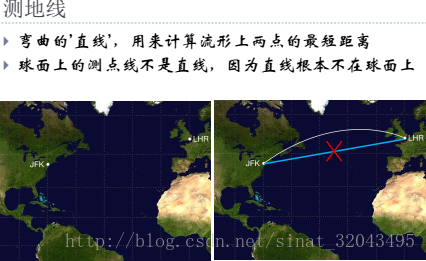
举个例子,从北京到上海有多远?你可以找一个地球仪,然后用一把能弯曲的软软的尺子,经过地球仪表面然后测量一下这两个点的距离。
但是如果我用一个直直的线,将地球仪从北京到上海洞穿,测量出一个更短的距离,你一定会觉得我疯了。显然对于“从北京到上海的距离”这件事,我们关注的是把三维地球展开成二维平面,然后测量的地表上的距离,而不是三维空间中球面上两个点的空间直线距离(相信没有人从北京到上海会挖一条直通上海的地道的!
将这个问题推广一些,假如说决策部门打算把一些离得比较近的城市聚成一堆,然后组建个大城市。这时候“远近”这个概念显然是指地表上的距离,因为说空间直线距离并没有什么意义。
而对于降维算法来说,如果使用传统的欧氏距离来作为距离尺度,显然会抛弃“数据的内部特征”。如果测量球面两点距离采用空间欧氏距离,那就会忽略掉“这是个球面”这个信息。
浅谈流形学习:http://blog.pluskid.org/?p=533
有时候经常会在 paper 里看到“嵌入在高维空间中的低维流形”,不过高维的数据对于我们这些可怜的低维生物来说总是很难以想像,所以最直观的例子通常都会是嵌入在三维空间中的二维或者一维流行。比如说一块布,可以把它看成一个二维平面,这是一个二维的欧氏空间,现在我们(在三维)中把它扭一扭,它就变成了一个流形(当然,不扭的时候,它也是一个流形,欧氏空间是流形的一种特殊情况)。
所以,直观上来讲,一个流形好比是一个 d 维的空间,在一个 m 维的空间中 (m > d) 被扭曲之后的结果。需要注意的是,流形并不是一个“形状”,而是一个“空间”,如果你觉得“扭曲的空间”难以想象,那么请再回忆之前一块布的例子。如果我没弄错的话,广义相对论似乎就是把我们的时空当作一个四维流(空间三维加上时间一维)形来研究的,引力就是这个流形扭曲的结果。当然,这些都是直观上的概念,其实流形并不需要依靠嵌入在一个“外围空间”而存在,稍微正式一点来说,一个 d 维的流形就是一个在任意点出局部同胚于(简单地说,就是正逆映射都是光滑的一一映射)欧氏空间 R^d 。
这里的图片来自同一张人脸(好吧,其实是人脸模型),每张图片是 64×64 的灰度图,如果把位图按照列(或行)拼起来,就可以得到一个 4096 维的向量,这样一来,每一张图片就可以看成是 4096 维欧氏空间中的一个点。很显然,并不是 4096 维空间中任意一个点都可以对应于一张人脸图片的,这就类似于球面的情形,我们可以假定所有可以是人脸的 4096 维向量实际上分布在一个 d 维 (d < 4096) 的子空间中。而特定到 Isomap 的人脸这个例子,实际上我们知道所有的 698 张图片是拍自同一个人脸(模型),不过是在不同的 pose 和光照下拍摄的,如果把 pose (上下和左右)当作两个自由度,而光照当作一个自由度,那么这些图片实际只有三个自由度,换句话说,存在一个类似于球面一样的参数方程(当然,解析式是没法写出来的),给定一组参数(也就是上下、左右的 pose 和光照这三个值),就可以生成出对应的 4096 维的坐标来。换句话说,这是一个嵌入在 4096 维欧氏空间中的一个 3 维流形,也就是3维流形在4096维的欧式空间被扭曲了的结果。 实际上,上面的那张图就是 Isomap 将这个数据集从 4096 维映射到 3 维空间中,并显示了其中 2 维的结果,图中的小点就是每个人脸在这个二维空间中对应的坐标位置,其中一些标红圈的点被选出来,并在旁边画上了该点对应的原始图片,可以很直观地看出这两个维度正好对应了 pose 的两个自由度平滑变化的结果。 就我目前所知,把流形引入到机器学习领域来主要有两种用途:一是将原来在欧氏空间中适用的算法加以改造,使得它工作在流形上,直接或间接地对流形的结构和性质加以利用;二是直接分析流形的结构,并试图将其映射到一个欧氏空间中,再在得到的结果上运用以前适用于欧氏空间的算法来进行学习。 这里 Isomap 正巧是一个非常典型的例子,因为它实际上是通过“改造一种原本适用于欧氏空间的算法”,达到了“将流形映射到一个欧氏空间”的目的。
Isomap 所改造的这个方法叫做 Multidimensional Scaling (MDS) ,MDS 是一种降维方法,它的目的就是使得降维之后的点两两之间的距离尽量不变(也就是和在原始空间中对应的两个点之间的距离要差不多)。只是 MDS 是针对欧氏空间设计的,对于距离的计算也是使用欧氏距离来完成的。如果数据分布在一个流形上的话,欧氏距离就不适用了。
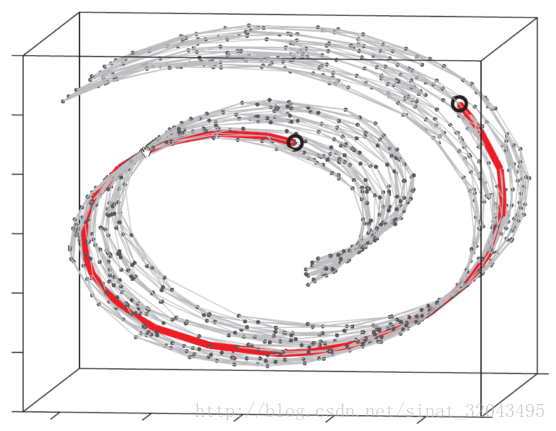
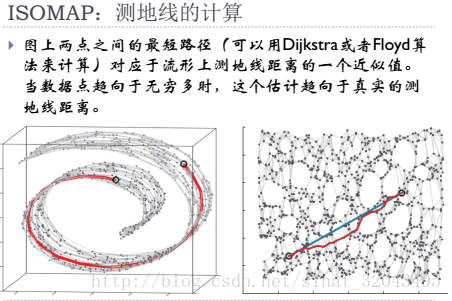
Isomap ,它主要做了一件事情,就是把 MDS 中原始空间中距离的计算从欧氏距离换为了流形上的测地距离。当然,如果流形的结构事先不知道的话,这个距离是没法算的,于是 Isomap 通过将数据点连接起来构成一个邻接 Graph 来离散地近似原来的流形,而测地距离也相应地通过 Graph 上的最短路径来近似了。如下图所示:
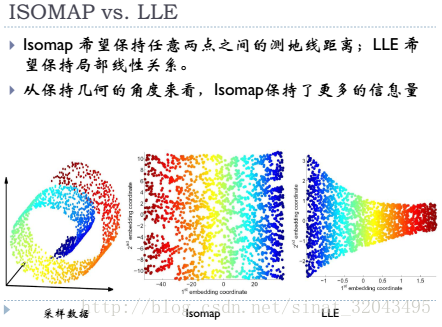
这个东西叫做Swiss Roll ,姑且把它看作一块卷起来的布好了。图中两个标黑圈的点,如果通过外围欧氏空间中的欧氏距离来计算的话,会是挨得很近的点,可是在流形上它们实际上是距离很远的点:红色的线是 Isomap 求出来的流形上的距离。可以想像,如果是原始的 MDS 的话,降维之后肯定会是很暴力地直接把它投影到二维空间中,完全无视流形结构,而 Isomap 则可以成功地将流形“展开”之后再做投影。
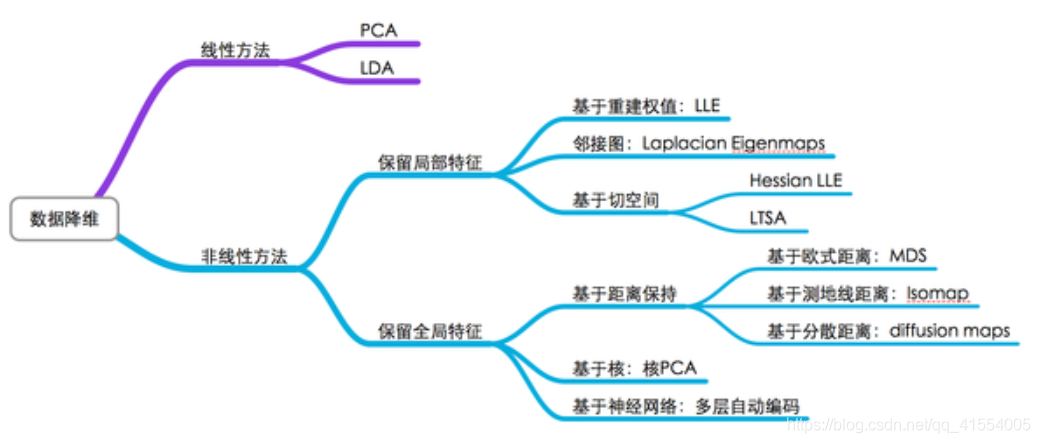
除了 Isomap 之外,Manifold Embedding 的算法还有很多很多,包括 Locally Linear Embedding 、Laplacian Eigenmaps 、Hessian Eigenmaps 、Local Tangent Space Alignment、Semidefinite Embedding (Maximum Variance Unfolding) 等等。
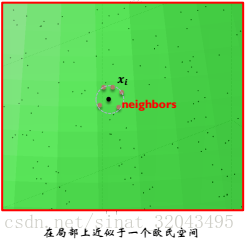
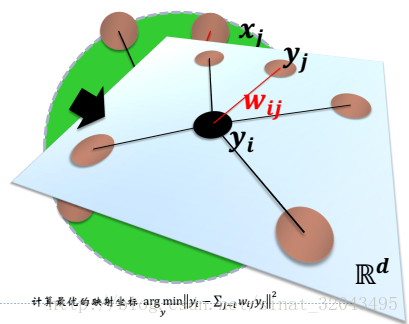
局部线性嵌入:假设数据中每个点可以由其近邻的几个点重构出来。降到低维,使样本仍能保持原来的重构关系,且重构系数也一样。
一个流形在很小的局部邻域上可以近似看成欧式的,就是局部线性的。那么,在小的局部邻域上,一个点就可以用它周围的点在最小二乘意义下最优的线性表示。局部线性嵌入把这个线性拟合的系数当成这个流形局部几何性质的刻画。那么一个好的低维表示,就应该也具有同样的局部几何,所以利用同样的线性表示的表达式。
所谓 Machine Learning 里的 Learning ,就是在建立一个模型之后,通过给定数据来求解模型参数。而 Manifold Learning 就是在模型里包含了对数据的流形假设。
2.相关的基本概念