一、前言

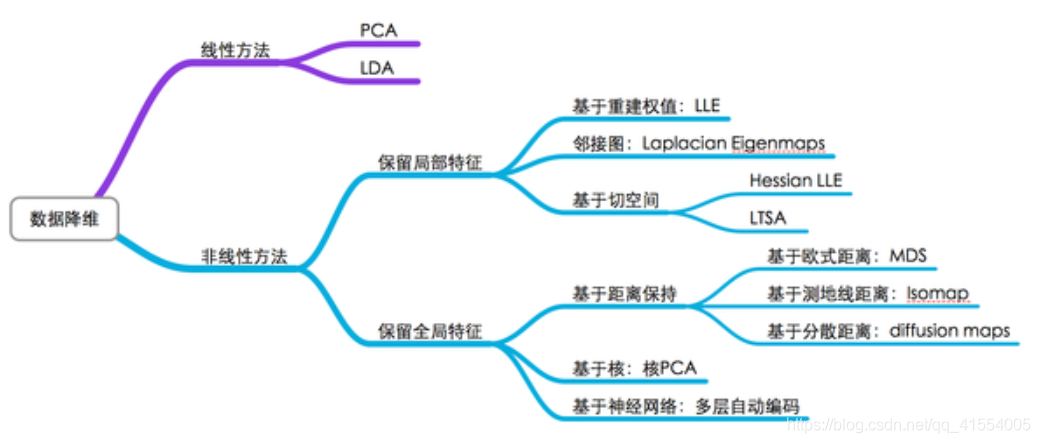
拉普拉斯特征映射是一种基于图的降维算法，它希望在原空间中相互间有相似关系的点，在降维后的空间中尽可能的靠近，从而在降维后仍能保持原有的数据结构信息。

二、主要步骤

拉普拉斯特征映射通过构建邻接矩阵为 $W$ （或叫相似矩阵）的图，来重构数据流形的局部结构特征。
主要思想是，如果两个数据样本 $i$ 和 $j$ 很相似，那么 $i$ 和 $j$ 在降维后子空间中应该与在原空间中一样，尽量接近。
假设数据实例的数目为 $n$ ，目标子空间的维数（即最终的降维目标的维度）为 $m$ 。定义 $n \times m$ 大小的矩阵 $Y$ ，其中每一个行向量 $y_i^T$ 是数据实例 $i$ 在目标 $m$ 维子空间中的向量表示（即降维后的数据实例 $i$ ）。我们的目的是让相似或相近的数据样本 $i$ 和 $j$ 在降维后的目标子空间里仍旧尽量接近。
具体步骤如下图所示：
在这里插入图片描述
1.确定拉普拉斯映射优化的目标函数： $\min \sum_{i, j}\left\|y_{i}-y_{j}\right\|^{2} W_{i j}$
其中 $W_{i j}$ 为构建邻接矩阵（或相似矩阵），距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，采用全连接法高斯核计算公式如下：
$w_{i j}=e^{-\frac{\left\|x_{i}-x_{j}\right\|_{2}^{2}}{2 \sigma^2}}$
2.目标函数优化：
$\begin{aligned} &\sum_{i=1}^{n} \sum_{j=1}^{n}\left\|y_{i}-y_{j}\right\|^{2} W_{i j} \\ &=\sum_{i=1}^{n} \sum_{j=1}^{n}\left(y_{i}^{T} y_{i}-2 y_{i}^{T} y_{j}+y_{j}^{T} y_{j}\right) W_{i j} \\ &=\sum_{i=1}^{n}\left(\sum_{j=1}^{n} W_{i j}\right) y_{i}^{T} y_{i}+\sum_{j=1}^{n}\left(\sum_{i=1}^{n} W_{i j}\right) y_{j}^{T} y_{j}-2 \sum_{i=1}^{n} \sum_{j=1}^{n} y_{i}^{T} y_{j} W_{i j} \\ &=2 \sum_{i=1}^{n} D_{i i} y_{i}^{T} y_{i}-2 \sum_{i=1}^{n} \sum_{j=1}^{n} y_{i}^{T} y_{j} W_{i j} \\ &=2 \operatorname{tr}\left(Y^{T} D Y\right)-2 \operatorname{tr}\left(Y^{T} W Y\right) \\ &=2 \operatorname{tr}\left[Y^{T}(D-W) Y\right] \\ &=2 \operatorname{tr}\left(Y^{T} L Y\right) \end{aligned}$
其中 $W$ 是图的邻接矩阵，对角矩阵 $D$ 是图的度矩阵( $D_{ii}=\sum_{j=1}^{n} W_{i j}$ )， $L = D - W$ 成为图的拉普拉斯矩阵。

变换后的拉普拉斯特征映射优化的目标函数如下：
$\min \operatorname{trace}\left(Y^{T} L Y\right), \quad \text { s.t. } Y^{T} D Y=I$

其中限制条件 $s.t. Y^{T} D Y=I$ 保证优化问题有解。

3.拉格朗日乘子法求解:
$\begin{aligned} &f(Y)=\operatorname{tr}\left(Y^{T} L Y\right)+\operatorname{tr}\left[\Lambda\left(Y^{T} D Y-I\right)\right] \\ &\frac{\partial f(Y)}{\partial Y}=L Y+L^{T} Y+D^{T} Y \Lambda^{T}+D Y \Lambda =2 L Y+2 D Y \Lambda=0 \\ &\therefore L Y=-D Y \Lambda \end{aligned}$