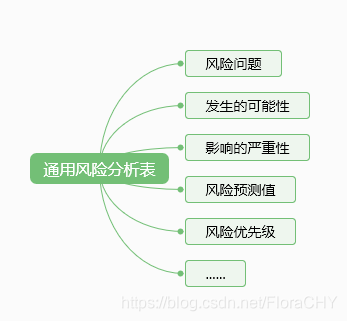
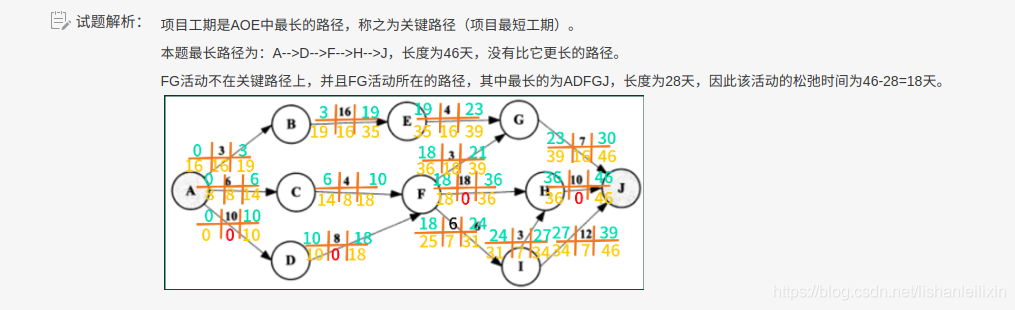
拉格朗日松弛算法在组合优化问题中的应用
- 轨道交通的应用背景
- 问题的叙述
- 模型的建立
- 侧线内的车辆调度算法
- Lagrangian松弛算法
- 数值实验
- 写在最后
轨道交通的应用背景
接下来说的是,拉格朗日松弛算法应用的背景,读者可以大概阅读。
近年来我国经济不断发展,国民消费水平与能力不断提高,与此同时中国铁路运输内外需的不确定因素众多,产品循环周期不断缩短,铁路货运出现节奏快、多样化等趋势。因为制造业、服务业在国家经济中的作用愈发不容忽视,越来越高的铁路货运需要与要求,给铁路货运调度带来了更多的困难与挑战。随着经济全球化和人类命运共同体理念深入人心,铁路货运的运输调度已经成为了重要的研究与发展的方向之一,且运输快捷方便、质量高速度快、运输量大、消耗代价小越来越成为铁路货运的代名词。
自20世纪50年代至今铁路货运发展的50多年来,中国铁路货运的集装箱总量已约占到世界总量的20%~25%。发展至今,中国铁路运输在中国经济发展中已经起到至关重要的作用了,其作为连接纽带不断由沿海拖到内陆经济的发展。中国铁路货运仰仗我们大型人口密集型国家的特点和完善的交通网络的优势,在21世纪中蓬勃发展。
不得不提出的是,中国铁路货运在发展中仍存在许多需要解决的问题。比如,铁路集装箱站的分布不合理,有时过于密集分布会造成资源浪费,而有些地方甚至出现了大半径无法及时找到铁路集装箱站的情况。基础设施过于薄弱导致铁路运输效率降低能耗增大,对集装箱流程一体化的实现造成了阻挠。集装箱空间大小与货物量大小的不匹配导致的运输空间资源浪费的问题,放在个体来看就是经典的背包问题。铁路货运集装箱造价还存在有不合理定价的现象,这可以归咎于仍不统一的铁路货运装配与调度系统。中国铁路运输发展不平衡尚待解决,沿海部分运输行业发达,内陆偏远地区的发展情况却极差。
在综合论述了中国铁路货运的背景与尚存在的问题之后,下面就对本文将要解决的问题提出叙述,讨论的核心重点在于铁路侧线内的列车调度。
问题的叙述
在基于此前的背景介绍下,我们就可以引出问题啦
现实生活中大型轨道调车场是本文章的研究背景,其大致背景是在一些庞大数量的车辆进站的情况
下,通过 轨道和调车场,在满足一定的约束条件,比如轨道种类约束,容量等等的情况下
,寻找目标函数 的最优质,按照给定的输出顺序。
已知车辆在主要终点站的离开和到达时间,以及每个轨道上的到达和离开时间。
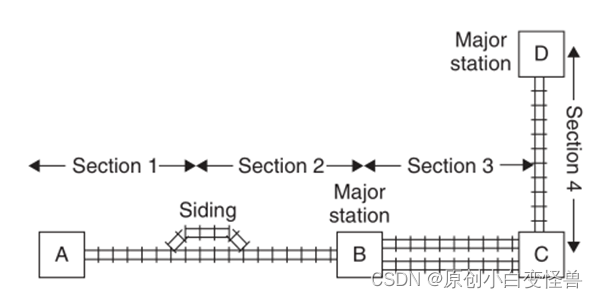
调车场轨道示意图
在大型轨道系统中,如图调车场轨道示意图所示,ABCD代表4个车站,而中间的轨道代表车辆行驶的轨道。AB,CD之间的轨道式单向的,BC之间的轨道是可以双向行驶的。在车站里只能完成先进先出的顺序操作。已知条件是轨道和主要调车场的列车进入和离开的时间。Siding为侧线,是平行于主线即轨道的一段辅助线路,其主要作用是用来会车和超车。
大多数的轨道都是单向行驶的,并且还会有一些时间上的要求。现实生活中时间的要求是很被重视的,物流迟到的时间越久后果越严重,所以相应的模型惩罚函数也要带权重地增加。综上所述,应该设计出尽可能好的算法来解决调度问题,最大限度地减少与原计划的偏差,并且尽可能满足时间上的要求。
下面提出一些问题背景下的约束条件。
① 轨道能够通行的车辆数无限大,侧线的容量无限大。
② 车辆有足够的能力在同一侧线中完成任意位置的一次调换超车,即无论距离多远均算做一次操作,付出的时间代价一致。
③ 有些列车有非常严格的时间表,如果延误超过预先规定的时间,就会招致非常高的罚款。
④ 只有侧线才能够完成列车的调度工作。
所有的这些限制使得问题变得更加复杂,从而对标准模型的通用性有了一定的限制。接下来我们建立数学模型来描述这个问题。
模型的建立

这是一个整数规划问题,即是离散的问题,因为文章的重点不在模型,所以就给出一个大概的框架,目标函数与约束条件,这些根据问题的实际去建立。
侧线内的车辆调度算法
侧线示意图


Lagrangian松弛算法



数值实验
我们的原始数据是
1,1,2,2,3,3,4,4,5,5,6,6,1,2,3,4,5,6,1,1,2,2,3,3,4,4,5,5,6,6
上面的队列为输入队列input,从左至右按顺序进站进行车辆的重组以达到出车的要求。输入队列的长度规模为30。
1,1,1,1,1,2,2,2,2,2
3,3,3,3,3,4,4,4,4,4
5,5,5,5,5,6,6,6,6,6
上面的三行是本次数值实验的输出数据即output,其规模大小为3×10。
Lagrangian松弛算法是一种估计,对问题的界或者是最坏可以得到的结果进行计算。
我们的结果是,直接车辆调度算法的调度代价是24次,经过拉格朗日松弛算法,可以优化到18次。
写在最后
本文的目的在于发表自己将拉格朗日松弛算法应用到组合优化问题中的想法,因为之前在网上搜集相关的blog和代码,可以说是少之又少。但拉格朗日松弛算法在知网、万方等网站上可以找到许多相关的论文,其大多应用于电气、物理问题等方面,而且如果真的细心去阅读理解论文的算法设计和问题背景,需要花不少的时间,代码的复现也存在着很大的问题。
另外,拉格朗日松弛算法在组合优化问题中,特别是以轨道交通背景下的文章和相关资料更是少之又少,这也是攥写本篇blog的原因。还有最后的一个原因是,正逢毕业季,许久没有动手写过论文和代码,现在提笔写来也是对大学生生涯的写作划上一个完美的句号。我深知这是一个持之以恒的过程,希望以后再回头看来能保持初心,一往无前。