一.影子价格
影子价格(shadow price),又称最优计划价格或计算价格。它是指依据一定原则确定的,能够反映投入物和产出物真实经济价值、反映市场供求状况、反映资源稀缺程度、使资源得到合理配置的价格。影子价格反映了社会经济处于某种最优状态下的资源稀缺程度和对最终产品的需求情况,有利于资源的最优配置。
当某种资源每增加一个单位,目标增加一定的单位,不同的资源有不同的边际贡献,这种资源的边际贡献就定义为该资源的影子价格。
二.互补松弛性质
举个栗子:
作者:覃含章
链接:https://www.zhihu.com/question/27471863/answer/123244103
来源:知乎
假设你是一个木匠,出售手工制作的木头桌子和木头椅子,简单起见,我们假定桌子的利润固定为一张10元,椅子为一把3元。生产一张桌子需要5单位木材和3单位时间,生产一把椅子需要2单位木材和1单位时间。且我们所有生产的桌子椅子都是能被卖掉的,先假设当月我们总共有200单位木材和90单位时间,现在你想要制定一个生产计划,让这个月的利润最大化。
那么这个生产计划问题显然可以用线性规划表达为如下,记作问题(P):

利用线性规划的对偶理论,问题(P)的对偶问题表达为如下,记作问题(D):
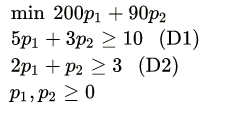
注意到原问题中变量代表生产桌子和椅子的数量,而在对偶问题中变量
代表的是原材料木材和时间的价格,或者说,原问题(P)中约束(P1)和(P2)对应的影子价格。
原问题(P)求的是给定生产约束,如何生产能使利润最大化。对对偶问题来说,对象是即是给定商品的单位利润,如何通过合理对原材料定价来使成本最小化。而这两个问题,显然是同一个问题。
为了说明这一点,我们同样求解对偶问题,得到最优解是,即木材的单位影子价格是0,时间的单位影子价格是3.33,这意味着什么呢?这意味着我们有的木材份量过量了,再增加木材对我们的最优解没有影响(这也是为什么它的影子价格是0),然而我们的时间资源却非常紧俏,哪怕多增加1单位的时间我们的总体利润也能提升(我们可以多生产1/3张桌子...或者说增加3单位时间好了,就可以多生生产1张桌子...)!
对应原问题(P)中,对应木材资源的约束(P1)在最优条件下是松的(不等号严格成立),而(P2)则是紧的(不等号其实是等号)。我们不妨计算得到:
我们不妨计算得到,,果然如此!
这便是互补松弛性的定义。如果在最优条件下一个约束不等式是松的,那么这个约束对应的影子价格为0。反过来说,如果这个约束对应的影子价格严格大于0,那么这个约束不等式一定是紧的。
所以,当你解完问题(P)的时候你必然就知道,且(D1)是紧的(因为
,注意(P)也是(D)的对偶问题),从而可以直接算出
,即不用再放到solver就可以手算出(D)的解。