对论文 Focused Trajectory Planning for Autonomous On-Road Driving的解析
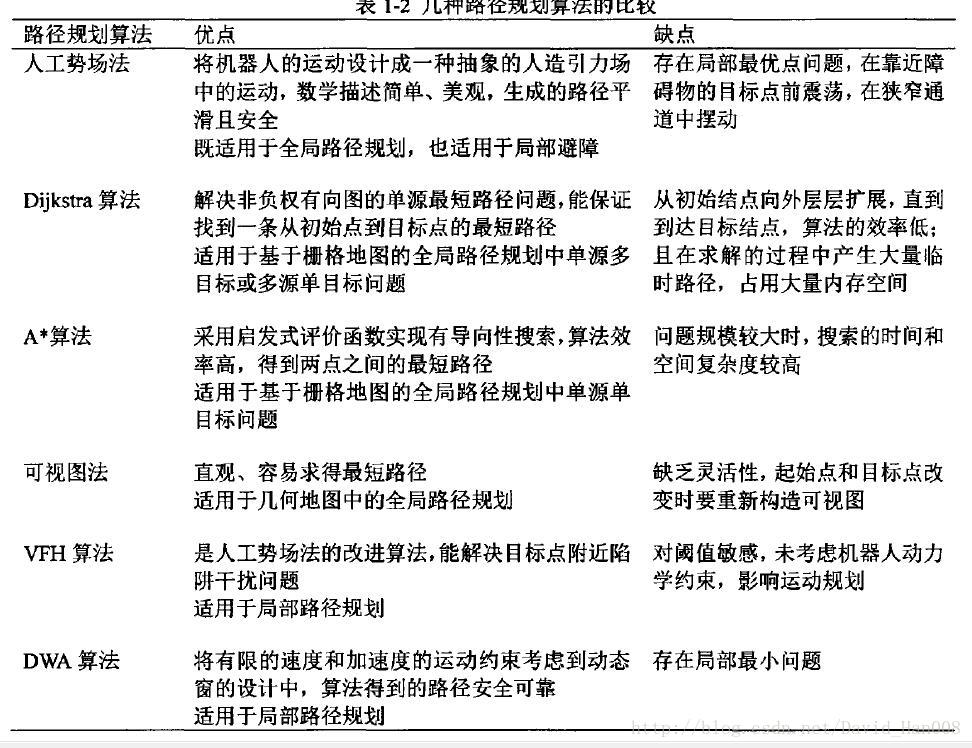
本文对 Focused Trajectory Planning for Autonomous On-Road Driving此篇论文进行解析,这批论文来自CMU Dolan小组的成果,此小组参加过Darpa城市赛并取得不错名次,所使用方法均基本在同一体系下。下面进行详解。
本文所论述的方法仅适用于静态障碍物避障,切不考虑碰撞检测成功性,属于简单不可行的方法,但具有一定参考意义。名义上这是对Focused Trajectory Planning for Autonomous On-Road Driving论文中的方法的简化。
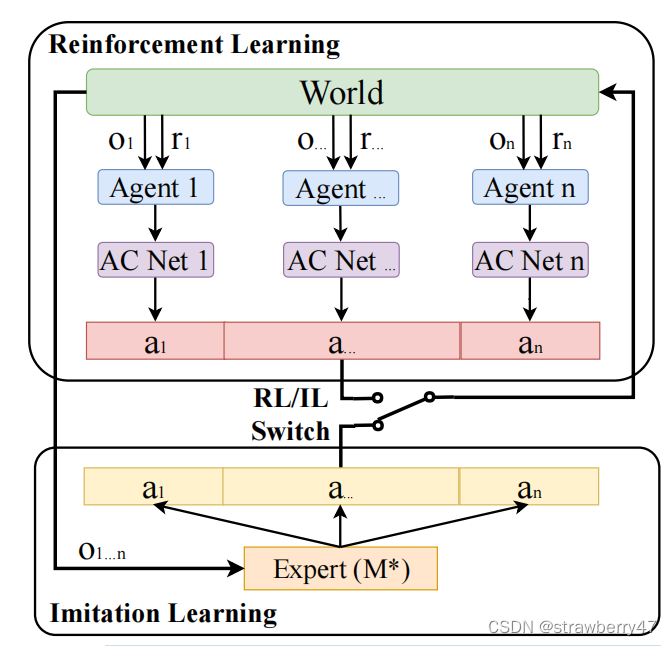
本方法的结构是这样的:
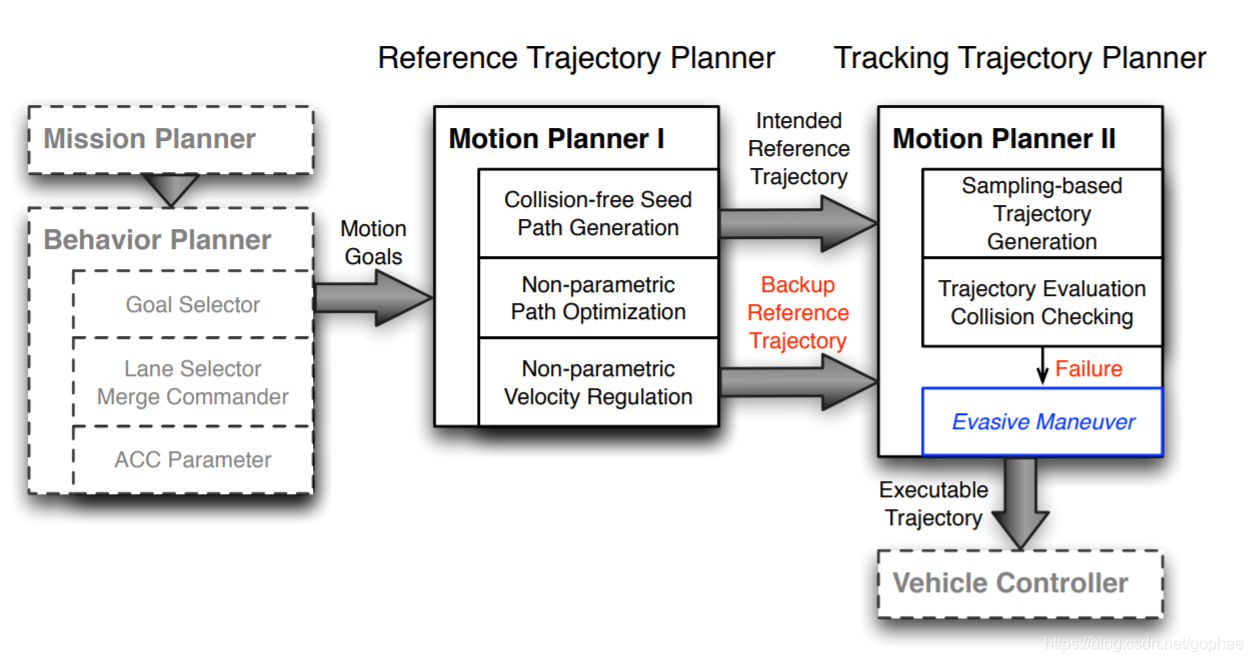
核心结构上由两个planner组成,第一个是为了减少计算量所设计的‘’粗糙‘’planner, 计算出一点直线段构成的0阶连续曲线,然后拟合成三阶多项式(曲率连续)。第二个planner 再上一个planner的基础上对曲线进行进一步优化,是曲率更加平滑,同时保证横向偏差尽量小。
第一个planner:
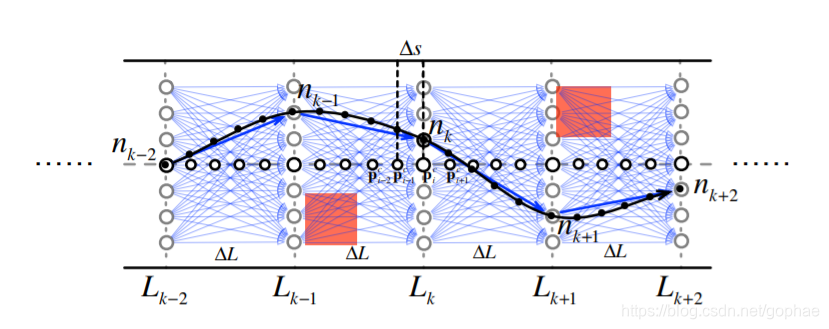
这张图表示了planner的工作流程,首先我们均匀采样参考线上的点,参考线一般选择路的中心线。参考线的采样长度用delta_s 表示, 在纵向我们均匀撒点,采样长度用delta_L表示。两者关系符合:
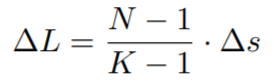
然后我们还要建立代价函数:
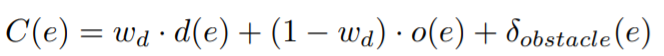
wd是weight, d 表示相邻的两个互相连接的点的长度,o表示lateral offset, 我们不希望这个曲线太长,这样运动效率就不高,同时我们也不希望曲线偏离中心线。最后一个delta是碰撞检测:
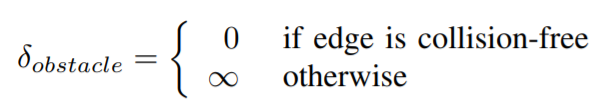
要解得目标函数是:
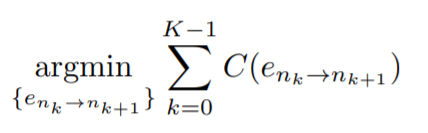
用动态规划的方式很容易就可以解出来,然后对这些点构成的直线段在进行一次三阶多项式拟合,获得一条粗糙的原始曲线。
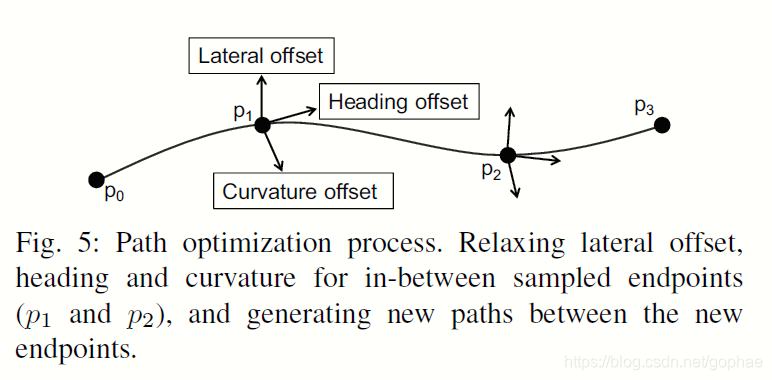
接下来就是进行第二次优化,下图表示了第二次优化和第一次的粗糙曲线的关系:
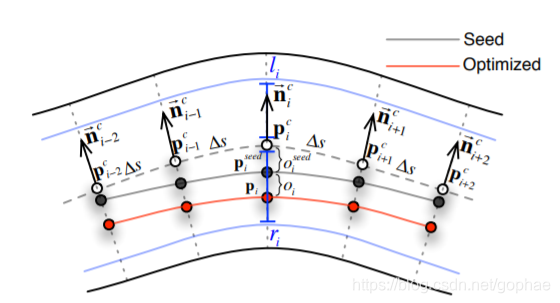
我们已经有了黑线,也就是上一个planner拟合出来的三阶多项式曲线,现在我们要在这个曲线的附件做一个优化,至于到底如何偏离就是我们需要优化的内容了,数学关系如下:
我们要在原有的基础上,在法向在移动一个距离Oi.
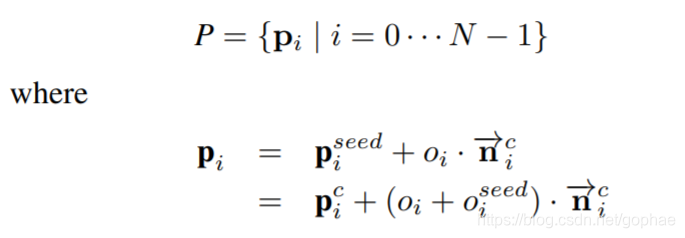
中间还有一些变量的关系如下:

意思是,首先一定距离一定是在路的边界以内的,还有几个关系式帮助你计算路的曲率。
最后我们要优化对象是:
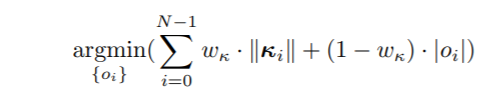
我们希望优化后的曲线累计曲率尽量小,同时我们还希望累计横向偏差尽量小。
从上面的优化过程可以看出,能够调节的两个参数也就是每个planner里面的weight了,下图给出了不同weight下的优化结果:
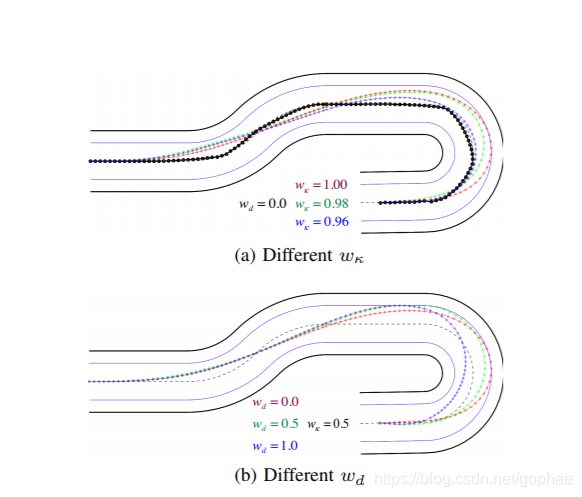
对原有曲率的优化效果也很明显:
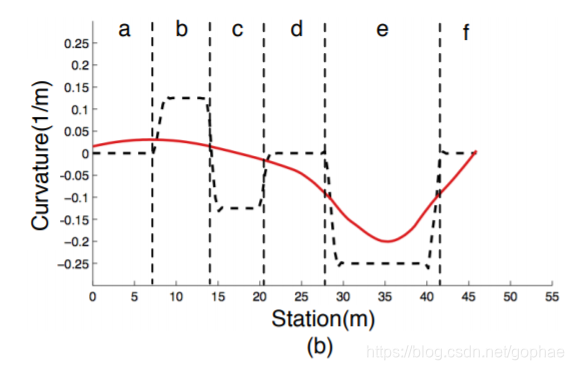
但是问题也很明显了,原来的三阶多项式是那个黑线,如果黑线旁边就有障碍物,优化出来的曲线极有可能发生碰撞。作者没有对优化后的曲线对于原曲线的偏移做出限制,同时对新曲线也不做碰撞检测,生成出来的优化曲线其实是不一定能通过碰撞检测的,也就是毫无作用的,不知道作者在做什么鬼。
速度方面,我们也要做一定的限制:

分别是:
道路限速,横向加速度限制,以及车辆本身处于舒适性考虑的加减速限制
第一个很好做,道路车速限制是提前给出的。
第二个计算一下曲率(这就是为什么上面我们特地计算出道路曲率的原因),安装公式给出此时的最高可行速度。
第三个按照以下算法即可: 意思是相邻的两个采样点的距离是知道的,最高的加减速限制也是已知的,这就决定了我们在两个采样点之间的最大的速度变化区间。按照这个理念计算出对应的车速即可。

总的来讲这个方法是有巨大缺陷的,怎么让他发了IV2013真的不懂。我考虑了一下解决方法还是有的,第一,优化的方向是需要被确定的,通常来讲,如果原有曲线往上偏离,那么障碍物一定在下面,那我直接设定优化过程必须是向上优化而不是向下优化,这可以避免大多数的碰撞情况。第二,如果还是可以随意优化我们在第二个planner里面还是要做一次碰撞检测的,但这次碰撞检测可以使用滞后碰撞检测,二次优化获得的结果如果不通过碰撞检测,就把次优解拿过来做碰撞检测,幸运的话在几次碰撞检测中就能获得可行解。