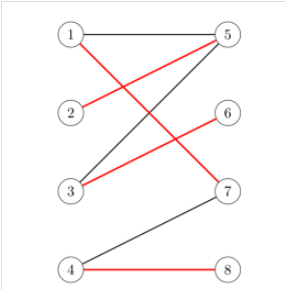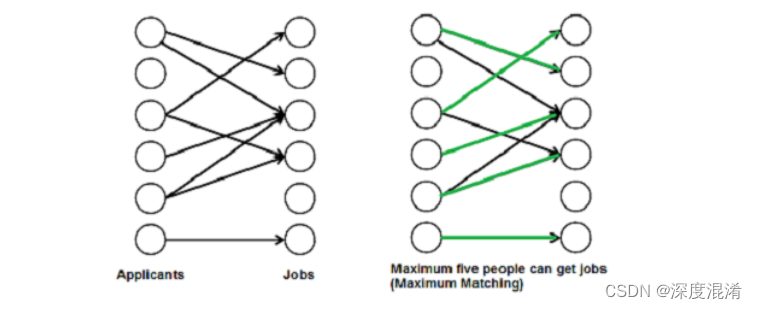
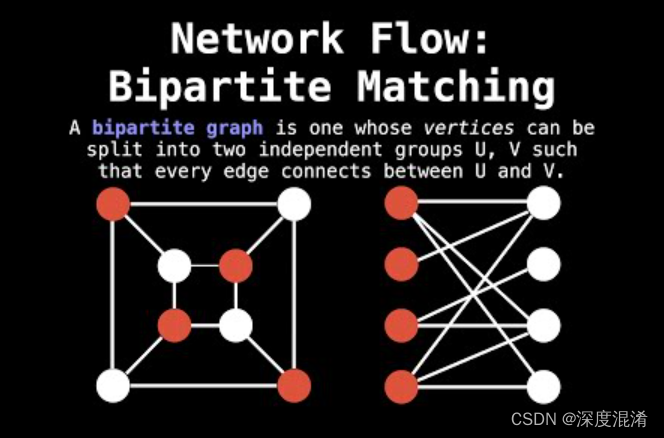
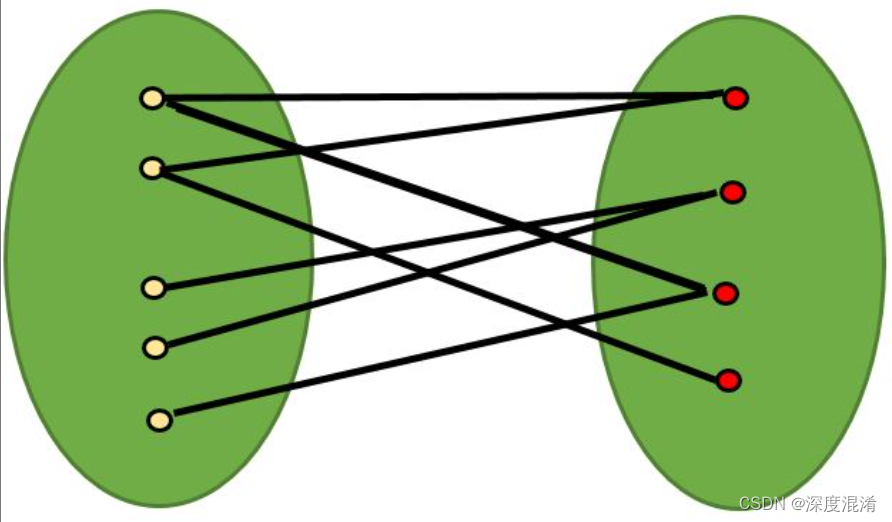
二部图中的匹配是一组边的选择方式，使两条边不共享一个端点。最大匹配是最大大小（最大边数）的匹配。在最大匹配中，如果向其添加任何边，则该边不再是匹配。对于给定的二部图，可以有多个最大匹配。

我们为什么在乎？

现实世界中有许多问题可以形成为二部匹配。例如，考虑以下问题：

“共有M个求职者和N个职位。每个求职者都有一部分他/她感兴趣的职位。每个职位空缺只能接受一个求职者，而一个求职者只能被任命一个职位。在中为求职者分配职位，以便尽可能多的求职者获得工作。”

我们强烈建议您先阅读以下帖子。“最大流问题的Ford-Fulkerson算法”

最大二部匹配和最大流问题：

最大二部匹配（MBP）问题可以通过将其转换为流网络来解决（请参阅此视频了解我们是如何得出此结论的）。以下是步骤。

最大匹配2

1） 构建流网络：流网络中必须有源和汇。因此，我们向所有申请者添加一个源，并从源添加边。类似地，将所有作业的边添加到接收器。每条边的容量标记为1个单位。

最大匹配2

2） 查找最大流量：我们使用Ford Fulkerson算法在步骤1中构建的流量网络中查找最大流量。最大流量实际上是我们正在寻找的MBP。

如何实施上述方法？

让我们首先定义输入和输出表单。输入采用Edmonds矩阵的形式，该矩阵是一个2D数组“bpGraph[M][N]”，其中有M行（针对M个求职者）和N列（针对N个工作）。如果第i个申请人对第j个工作感兴趣，则bpGraph[i][j]的值为1，否则为0。

输出是能找到工作的最大人数。

实现这一点的一种简单方法是创建一个矩阵，该矩阵表示具有M+N+2个顶点的有向图的邻接矩阵表示。为矩阵调用fordFulkerson（）。此实现需要O（（M+N）*（M+N））额外空间。

利用图是二部图且每条边的容量为0或1的事实，可以减少额外空间并简化代码。其想法是使用DFS遍历为申请人找到一份工作（类似于福特·富尔克森（FordFulkerson）中的扩充路径）。我们为每个申请者调用bpm（），bpm（）是一个基于DFS的函数，它尝试所有可能的方法来为申请者分配工作。

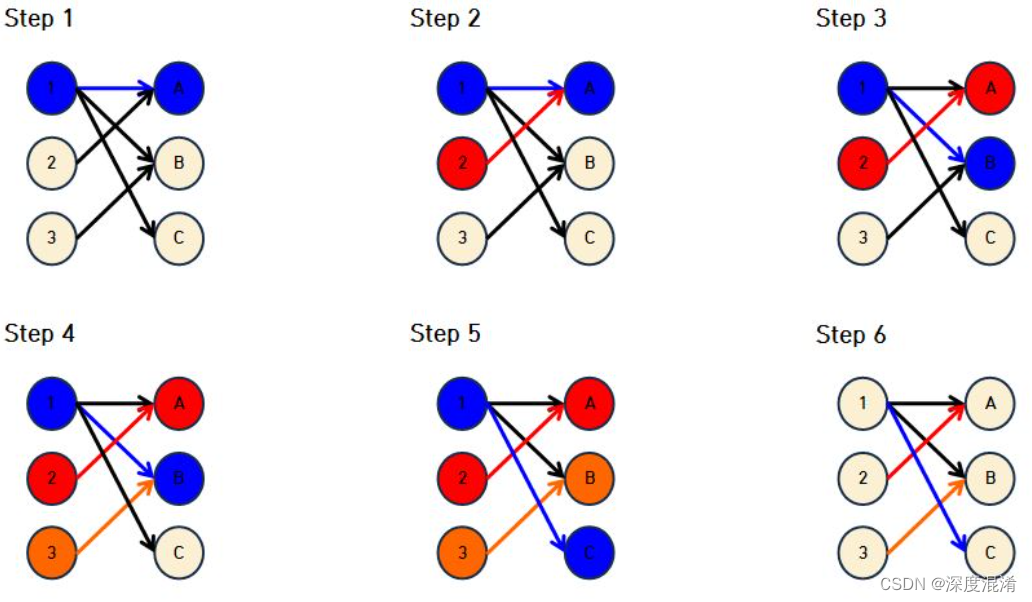
在bpm（）中，我们会一个接一个地尝试申请人“u”感兴趣的所有工作，直到我们找到一份工作，或者所有工作都是在运气不佳的情况下尝试的。对于我们尝试的每一项工作，我们都会遵循以下原则。

如果工作没有分配给任何人，我们只需将其分配给申请人并返回true。如果一个作业分配给了其他人，比如x，那么我们递归地检查x是否可以分配给其他作业。为了确保x不再获得相同的工作，我们在递归调用x之前将作业标记为“v”。如果x可以获得其他作业，我们将更改作业“v”的申请人并返回true。我们使用一个数组maxR[0..N-1]，它存储分配给不同工作的申请者。

如果bmp（）返回true，则表示流网络中有一个扩充路径，并且在maxBPM（）中的结果中添加了1个流单元。

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public static partial class Algorithm_Gallery{private static bool Maximum_Bipartite_Matching_Utility(bool[,] bpGraph, int u, bool[] seen, int[] matchR){int N = bpGraph.GetLength(1);for (int v = 0; v < N; v++){if (bpGraph[u, v] && !seen[v]){seen[v] = true;if (matchR[v] < 0 || Maximum_Bipartite_Matching_Utility(bpGraph, matchR[v], seen, matchR)){matchR[v] = u;return true;}}}return false;}public static int Maximum_Bipartite_Matching(bool[,] bpGraph){int M = bpGraph.GetLength(0);int N = bpGraph.GetLength(1);int[] matchR = new int[N];for (int i = 0; i < N; i++){matchR[i] = -1;}int result = 0;for (int u = 0; u < M; u++){bool[] seen = new bool[N];for (int i = 0; i < N; i++){seen[i] = false;}if (Maximum_Bipartite_Matching_Utility(bpGraph, u, seen, matchR)){result++;}}return result;}}public static partial class GalleryDrive{public static string MBM(){bool[,] bpGraph = new bool[,] {{ false,  true,  true, false, false, false },{ true,  false, false,  true, false, false },{ false, false,  true, false, false, false },{ false, false,  true,  true, false, false },{ false, false, false, false, false, false },{ false, false, false, false, false,  true }};return ("Maximum number of applicants that can get job is " + Algorithm_Gallery.Maximum_Bipartite_Matching(bpGraph));}}
}