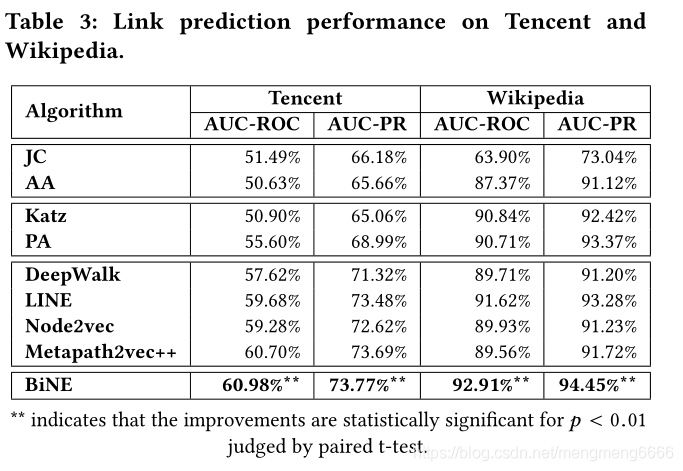
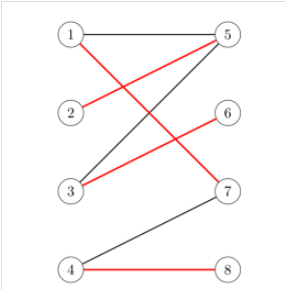
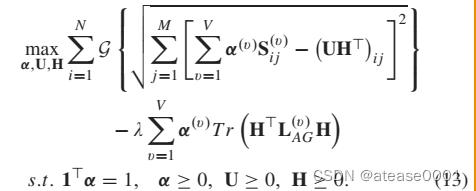【一致性仿真】Fixed-time bipartite consensus of multi-agent systems with disturbances

文章链接：Fixed-time bipartite consensus of multi-agent systems with disturbances
仿真图Fig2：
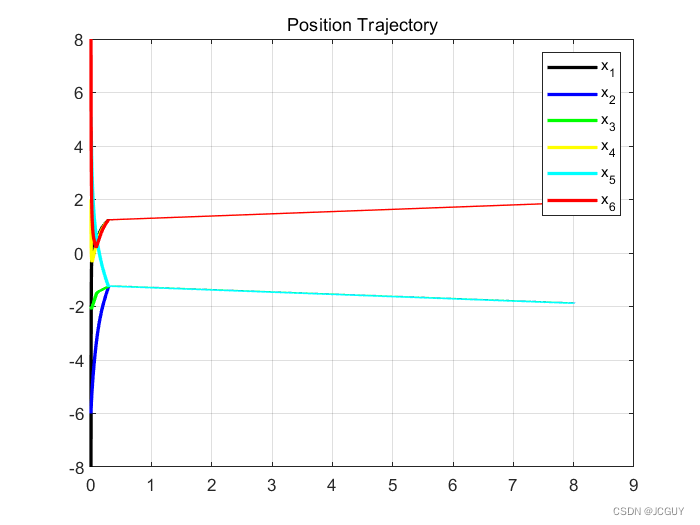
在这里插入图片描述
MATLAB代码：

% Fixed-time bipartite consensus of multi-agent systems with disturbances
% author:JCGUY
% date:2022-04-20
clear
clc%% 
tBegin = 0;
dT     = 0.001;
tFinal = 8;
times  = (tFinal - tBegin) / dT;
time   = 1;
t(1,1) = 0;A = [ 0 -1  0  6  0  7;-1  0  2  0  0  0;0  2  0 -3  0  0;6  0 -3  0 -4  0;0  0  0 -4  0 -2;7  0  0  0 -2  0];X(:,1) = [-8 -6 -2 2 6 8]';
% X(:,1) = [-20 -15 10 -6 20 6]';
U(:,1) = [0, 0, 0, 0, 0]';
Usum(:,1) = [0, 0, 0, 0, 0]';
mu=0.5;eta=0.6;alpha=6.1;m=3;%提供的参数%% 迭代公式，收敛计算
for i=1:timest(:,i+1) = t(:,i) + dT;% 控制输入分别为 atan()Usum(1, i)= A(1,2)*(X(2, i)-sign(A(1,2))*X(1, i)) + A(1,4)*(X(4, i)-sign(A(1,4))*X(1, i)) + A(1,6)*(X(6, i)-sign(A(1,6))*X(1, i));U(1, i) = mu*sign(Usum(1, i))*abs(Usum(1, i))^(2-1/m)+eta*sign(Usum(1, i))*abs(Usum(1, i))^(1/m)+alpha*sign(Usum(1, i)) + 0.1;Usum(2, i)= A(2,1)*(X(2, i)-sign(A(2,1))*X(1, i)) + A(2,3)*(X(3, i)-sign(A(2,3))*X(2, i));U(2, i) = mu*sign(Usum(2, i))*abs(Usum(2, i))^(2-1/m)+eta*sign(Usum(2, i))*abs(Usum(2, i))^(1/m)+alpha*sign(Usum(2, i)) + 0.1;Usum(3, i)= A(3,2)*(X(2, i)-sign(A(3,2))*X(3, i)) + A(3,4)*(X(4, i)-sign(A(3,4))*X(3, i));U(3, i) = mu*sign(Usum(3, i))*abs(Usum(3, i))^(2-1/m)+eta*sign(Usum(3, i))*abs(Usum(3, i))^(1/m)+alpha*sign(Usum(3, i)) + 0.1;Usum(4, i)= A(4,1)*(X(1, i)-sign(A(4,1))*X(4, i)) + A(4,3)*(X(3, i)-sign(A(4,3))*X(4, i)) + A(4,5)*(X(5, i)-sign(A(4,5))*X(4, i));U(4, i) = mu*sign(Usum(4, i))*abs(Usum(4, i))^(2-1/m)+eta*sign(Usum(4, i))*abs(Usum(4, i))^(1/m)+alpha*sign(Usum(4, i)) + 0.1;   Usum(5, i)= A(5,4)*(X(4, i)-sign(A(5,4))*X(5, i)) + A(5,6)*(X(6, i)-sign(A(5,6))*X(5, i));U(5, i) = mu*sign(Usum(5, i))*abs(Usum(5, i))^(2-1/m)+eta*sign(Usum(5, i))*abs(Usum(5, i))^(1/m)+alpha*sign(Usum(5, i)) + 0.1;Usum(6, i)= A(6,1)*(X(1, i)-sign(A(6,1))*X(6, i)) + A(6,5)*(X(5, i)-sign(A(6,5))*X(6, i));U(6, i) = mu*sign(Usum(6, i))*abs(Usum(6, i))^(2-1/m)+eta*sign(Usum(6, i))*abs(Usum(6, i))^(1/m)+alpha*sign(Usum(6, i)) + 0.1;X(:,i+1) = X(:,i) + U(:,i)*dT;end%% 绘图
subplot(1,1,1)
plot(t,X(1,:),'k','linewidth',2.0); hold on % x1
plot(t,X(2,:),'b','linewidth',2.0); hold on % x2
plot(t,X(3,:),'g','linewidth',2.0); hold on % x3
plot(t,X(4,:),'y','linewidth',2.0); hold on % x4
plot(t,X(5,:),'c','linewidth',2.0); hold on % x5
plot(t,X(6,:),'r','linewidth',2.0); hold on % x5
title('Position Trajectory');
legend("x_1", "x_2", "x_3", "x_4", "x_5", "x_6");
%axis([0 8 -8 8]); 
grid on; box on;

仿真图Fig3：
在这里插入图片描述
MATLAB代码：

% Fixed-time bipartite consensus of multi-agent systems with disturbances
% author:JCGUY
% date:2022-04-20
clear
clc%% 
tBegin = 0;
dT     = 0.001;
tFinal = 8;
times  = (tFinal - tBegin) / dT;
time   = 1;
t(1,1) = 0;A = [ 0 -1  0  6  0  7;-1  0  2  0  0  0;0  2  0 -3  0  0;6  0 -3  0 -4  0;0  0  0 -4  0 -2;7  0  0  0 -2  0];X(:,1) = [-8 -6 -2 2 6 8]';
% X(:,1) = [-20 -15 10 -6 20 6]';
U(:,1) = [0, 0, 0, 0, 0]';
Usum(:,1) = [0, 0, 0, 0, 0]';
mu=0.5;eta=0.6;alpha=6.1;m=3;%提供的参数%% 迭代公式，收敛计算
for i=1:timest(:,i+1) = t(:,i) + dT;% 控制输入分别为 atan()Usum(1, i)= A(1,2)*(X(2, i)-sign(A(1,2))*X(1, i)) + A(1,4)*(X(4, i)-sign(A(1,4))*X(1, i)) + A(1,6)*(X(6, i)-sign(A(1,6))*X(1, i));U(1, i) = mu*sign(Usum(1, i))*abs(Usum(1, i))^(2-1/m)+eta*sign(Usum(1, i))*abs(Usum(1, i))^(1/m)+alpha*sign(Usum(1, i)) + sin(1*i);Usum(2, i)= A(2,1)*(X(2, i)-sign(A(2,1))*X(1, i)) + A(2,3)*(X(3, i)-sign(A(2,3))*X(2, i));U(2, i) = mu*sign(Usum(2, i))*abs(Usum(2, i))^(2-1/m)+eta*sign(Usum(2, i))*abs(Usum(2, i))^(1/m)+alpha*sign(Usum(2, i)) + sin(2*i);Usum(3, i)= A(3,2)*(X(2, i)-sign(A(3,2))*X(3, i)) + A(3,4)*(X(4, i)-sign(A(3,4))*X(3, i));U(3, i) = mu*sign(Usum(3, i))*abs(Usum(3, i))^(2-1/m)+eta*sign(Usum(3, i))*abs(Usum(3, i))^(1/m)+alpha*sign(Usum(3, i)) + sin(3*i);Usum(4, i)= A(4,1)*(X(1, i)-sign(A(4,1))*X(4, i)) + A(4,3)*(X(3, i)-sign(A(4,3))*X(4, i)) + A(4,5)*(X(5, i)-sign(A(4,5))*X(4, i));U(4, i) = mu*sign(Usum(4, i))*abs(Usum(4, i))^(2-1/m)+eta*sign(Usum(4, i))*abs(Usum(4, i))^(1/m)+alpha*sign(Usum(4, i)) + sin(4*i);   Usum(5, i)= A(5,4)*(X(4, i)-sign(A(5,4))*X(5, i)) + A(5,6)*(X(6, i)-sign(A(5,6))*X(5, i));U(5, i) = mu*sign(Usum(5, i))*abs(Usum(5, i))^(2-1/m)+eta*sign(Usum(5, i))*abs(Usum(5, i))^(1/m)+alpha*sign(Usum(5, i)) + sin(5*i);Usum(6, i)= A(6,1)*(X(1, i)-sign(A(6,1))*X(6, i)) + A(6,5)*(X(5, i)-sign(A(6,5))*X(6, i));U(6, i) = mu*sign(Usum(6, i))*abs(Usum(6, i))^(2-1/m)+eta*sign(Usum(6, i))*abs(Usum(6, i))^(1/m)+alpha*sign(Usum(6, i)) + sin(6*i);X(:,i+1) = X(:,i) + U(:,i)*dT;end%% 绘图
subplot(1,1,1)
plot(t,X(1,:),'k','linewidth',2.0); hold on % x1
plot(t,X(2,:),'b','linewidth',2.0); hold on % x2
plot(t,X(3,:),'g','linewidth',2.0); hold on % x3
plot(t,X(4,:),'y','linewidth',2.0); hold on % x4
plot(t,X(5,:),'c','linewidth',2.0); hold on % x5
plot(t,X(6,:),'r','linewidth',2.0); hold on % x5
title('Position Trajectory');
legend("x_1", "x_2", "x_3", "x_4", "x_5", "x_6");
%axis([0 8 -8 8]); 
grid on; box on;

仿真图Fig4：
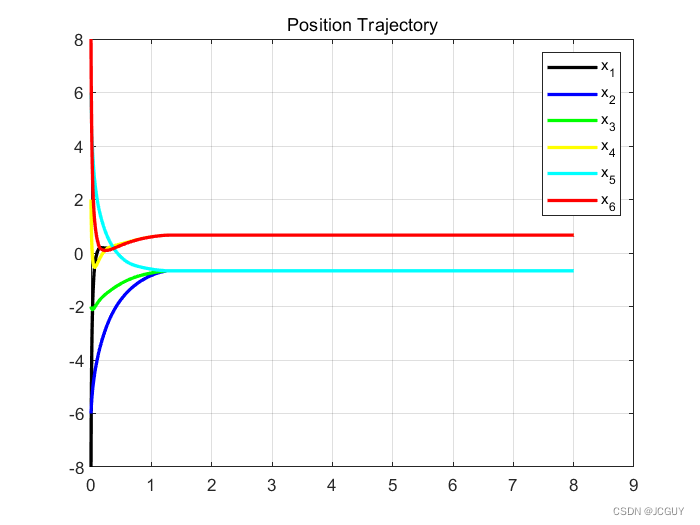
在这里插入图片描述

MATLAB代码：

% Fixed-time bipartite consensus of multi-agent systems with disturbances
% author:JCGUY
% date:2022-04-20
clear
clc%% 
tBegin = 0;
dT     = 0.001;
tFinal = 8;
times  = (tFinal - tBegin) / dT;
time   = 1;
t(1,1) = 0;A = [ 0 -1  0  6  0  7;-1  0  2  0  0  0;0  2  0 -3  0  0;6  0 -3  0 -4  0;0  0  0 -4  0 -2;7  0  0  0 -2  0];X(:,1) = [-8 -6 -2 2 6 8]';
% X(:,1) = [-20 -15 10 -6 20 6]';
U(:,1) = [0, 0, 0, 0, 0]';
mu=0.5;eta=0.6;alpha=6.1;m=3;%提供的参数%% 迭代公式，收敛计算
for i=1:timest(:,i+1) = t(:,i) + dT;% 控制输入分别为 atan()U(1, i) = mu*A(1,2)* sign(X(2, i)-sign(A(1,2))*X(1, i))*abs(X(2, i)-sign(A(1,2))*X(1, i))^(2-1/m)+...mu*A(1,4)* sign(X(4, i)-sign(A(1,4))*X(1, i))*abs(X(4, i)-sign(A(1,4))*X(1, i))^(2-1/m)+...mu*A(1,6)* sign(X(6, i)-sign(A(1,6))*X(1, i))*abs(X(6, i)-sign(A(1,6))*X(1, i))^(2-1/m)+...eta*A(1,2)* sign(X(2, i)-sign(A(1,2))*X(1, i))*abs(X(2, i)-sign(A(1,2))*X(1, i))^(1/m)+...eta*A(1,4)* sign(X(4, i)-sign(A(1,4))*X(1, i))*abs(X(4, i)-sign(A(1,4))*X(1, i))^(1/m)+...eta*A(1,6)* sign(X(6, i)-sign(A(1,6))*X(1, i))*abs(X(6, i)-sign(A(1,6))*X(1, i))^(1/m);U(2, i) = mu*A(2,1)* sign(X(1, i)-sign(A(2,1))*X(2, i))*abs(X(1, i)-sign(A(2,1))*X(2, i))^(2-1/m)+...mu*A(2,3)* sign(X(3, i)-sign(A(2,3))*X(2, i))*abs(X(3, i)-sign(A(2,3))*X(2, i))^(2-1/m)+...eta*A(2,1)* sign(X(1, i)-sign(A(2,1))*X(2, i))*abs(X(1, i)-sign(A(2,1))*X(2, i))^(1/m)+...eta*A(2,3)* sign(X(3, i)-sign(A(2,3))*X(2, i))*abs(X(3, i)-sign(A(2,3))*X(2, i))^(1/m);U(3, i) = mu*A(3,2)* sign(X(2, i)-sign(A(3,2))*X(3, i))*abs(X(2, i)-sign(A(3,2))*X(3, i))^(2-1/m)+...mu*A(3,4)* sign(X(4, i)-sign(A(3,4))*X(3, i))*abs(X(4, i)-sign(A(3,4))*X(3, i))^(2-1/m)+...eta*A(3,2)* sign(X(2, i)-sign(A(3,2))*X(3, i))*abs(X(2, i)-sign(A(3,2))*X(3, i))^(1/m)+...eta*A(3,4)* sign(X(4, i)-sign(A(3,4))*X(3, i))*abs(X(4, i)-sign(A(3,4))*X(3, i))^(1/m);U(4, i) = mu*A(4,1)* sign(X(1, i)-sign(A(4,1))*X(4, i))*abs(X(1, i)-sign(A(4,1))*X(4, i))^(2-1/m)+...mu*A(4,3)* sign(X(3, i)-sign(A(4,3))*X(4, i))*abs(X(3, i)-sign(A(4,3))*X(4, i))^(2-1/m)+...mu*A(4,5)* sign(X(5, i)-sign(A(4,5))*X(4, i))*abs(X(5, i)-sign(A(4,5))*X(4, i))^(2-1/m)+...eta*A(4,1)* sign(X(1, i)-sign(A(4,1))*X(4, i))*abs(X(1, i)-sign(A(4,1))*X(4, i))^(1/m)+...eta*A(4,3)* sign(X(3, i)-sign(A(4,3))*X(4, i))*abs(X(3, i)-sign(A(4,3))*X(4, i))^(1/m)+...eta*A(4,5)* sign(X(5, i)-sign(A(4,5))*X(4, i))*abs(X(5, i)-sign(A(4,5))*X(4, i))^(1/m);U(5, i) = mu*A(5,4)* sign(X(4, i)-sign(A(5,4))*X(5, i))*abs(X(4, i)-sign(A(5,4))*X(5, i))^(2-1/m)+...mu*A(5,6)* sign(X(6, i)-sign(A(5,6))*X(5, i))*abs(X(6, i)-sign(A(5,6))*X(5, i))^(2-1/m)+...eta*A(5,4)* sign(X(4, i)-sign(A(5,4))*X(5, i))*abs(X(4, i)-sign(A(5,4))*X(5, i))^(1/m)+...eta*A(5,6)* sign(X(6, i)-sign(A(5,6))*X(5, i))*abs(X(6, i)-sign(A(5,6))*X(5, i))^(1/m); U(6, i) = mu*A(6,1)* sign(X(1, i)-sign(A(6,1))*X(6, i))*abs(X(1, i)-sign(A(6,1))*X(6, i))^(2-1/m)+...mu*A(6,5)* sign(X(5, i)-sign(A(6,5))*X(6, i))*abs(X(5, i)-sign(A(6,5))*X(6, i))^(2-1/m)+...eta*A(6,1)* sign(X(1, i)-sign(A(6,1))*X(6, i))*abs(X(1, i)-sign(A(6,1))*X(6, i))^(1/m)+...eta*A(6,5)* sign(X(5, i)-sign(A(6,5))*X(6, i))*abs(X(5, i)-sign(A(6,5))*X(6, i))^(1/m);X(:,i+1) = X(:,i) + U(:,i)*dT;end%% 绘图
subplot(1,1,1)
plot(t,X(1,:),'k','linewidth',2.0); hold on % x1
plot(t,X(2,:),'b','linewidth',2.0); hold on % x2
plot(t,X(3,:),'g','linewidth',2.0); hold on % x3
plot(t,X(4,:),'y','linewidth',2.0); hold on % x4
plot(t,X(5,:),'c','linewidth',2.0); hold on % x5
plot(t,X(6,:),'r','linewidth',2.0); hold on % x5
title('Position Trajectory');
legend("x_1", "x_2", "x_3", "x_4", "x_5", "x_6");
%axis([0 8 -8 8]); 
grid on; box on;

仿真图Fig5：
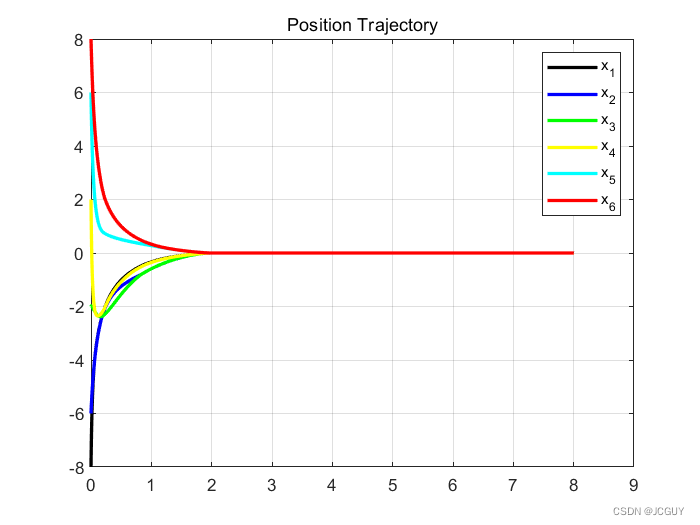
在这里插入图片描述

MATLAB代码：

% Fixed-time bipartite consensus of multi-agent systems with disturbances
% author:JCGUY
% date:2022-04-20
clear
clc%% 
tBegin = 0;
dT     = 0.001;
tFinal = 8;
times  = (tFinal - tBegin) / dT;
time   = 1;
t(1,1) = 0;A = [ 0 -1  0  6  0 -7;-1  0  2  0  0  0;0  2  0  3  0  0;6  0  3  0 -4  0;0  0  0 -4  0 -2;-7  0  0  0 -2  0];X(:,1) = [-8 -6 -2 2 6 8]';
% X(:,1) = [-20 -15 10 -6 20 6]';
U(:,1) = [0, 0, 0, 0, 0]';
mu=0.5;eta=0.6;alpha=6.1;m=3;%提供的参数%% 迭代公式，收敛计算
for i=1:timest(:,i+1) = t(:,i) + dT;% 控制输入分别为 atan()U(1, i) = mu*A(1,2)* sign(X(2, i)-sign(A(1,2))*X(1, i))*abs(X(2, i)-sign(A(1,2))*X(1, i))^(2-1/m)+...mu*A(1,4)* sign(X(4, i)-sign(A(1,4))*X(1, i))*abs(X(4, i)-sign(A(1,4))*X(1, i))^(2-1/m)+...mu*A(1,6)* sign(X(6, i)-sign(A(1,6))*X(1, i))*abs(X(6, i)-sign(A(1,6))*X(1, i))^(2-1/m)+...eta*A(1,2)* sign(X(2, i)-sign(A(1,2))*X(1, i))*abs(X(2, i)-sign(A(1,2))*X(1, i))^(1/m)+...eta*A(1,4)* sign(X(4, i)-sign(A(1,4))*X(1, i))*abs(X(4, i)-sign(A(1,4))*X(1, i))^(1/m)+...eta*A(1,6)* sign(X(6, i)-sign(A(1,6))*X(1, i))*abs(X(6, i)-sign(A(1,6))*X(1, i))^(1/m);U(2, i) = mu*A(2,1)* sign(X(1, i)-sign(A(2,1))*X(2, i))*abs(X(1, i)-sign(A(2,1))*X(2, i))^(2-1/m)+...mu*A(2,3)* sign(X(3, i)-sign(A(2,3))*X(2, i))*abs(X(3, i)-sign(A(2,3))*X(2, i))^(2-1/m)+...eta*A(2,1)* sign(X(1, i)-sign(A(2,1))*X(2, i))*abs(X(1, i)-sign(A(2,1))*X(2, i))^(1/m)+...eta*A(2,3)* sign(X(3, i)-sign(A(2,3))*X(2, i))*abs(X(3, i)-sign(A(2,3))*X(2, i))^(1/m);U(3, i) = mu*A(3,2)* sign(X(2, i)-sign(A(3,2))*X(3, i))*abs(X(2, i)-sign(A(3,2))*X(3, i))^(2-1/m)+...mu*A(3,4)* sign(X(4, i)-sign(A(3,4))*X(3, i))*abs(X(4, i)-sign(A(3,4))*X(3, i))^(2-1/m)+...eta*A(3,2)* sign(X(2, i)-sign(A(3,2))*X(3, i))*abs(X(2, i)-sign(A(3,2))*X(3, i))^(1/m)+...eta*A(3,4)* sign(X(4, i)-sign(A(3,4))*X(3, i))*abs(X(4, i)-sign(A(3,4))*X(3, i))^(1/m);U(4, i) = mu*A(4,1)* sign(X(1, i)-sign(A(4,1))*X(4, i))*abs(X(1, i)-sign(A(4,1))*X(4, i))^(2-1/m)+...mu*A(4,3)* sign(X(3, i)-sign(A(4,3))*X(4, i))*abs(X(3, i)-sign(A(4,3))*X(4, i))^(2-1/m)+...mu*A(4,5)* sign(X(5, i)-sign(A(4,5))*X(4, i))*abs(X(5, i)-sign(A(4,5))*X(4, i))^(2-1/m)+...eta*A(4,1)* sign(X(1, i)-sign(A(4,1))*X(4, i))*abs(X(1, i)-sign(A(4,1))*X(4, i))^(1/m)+...eta*A(4,3)* sign(X(3, i)-sign(A(4,3))*X(4, i))*abs(X(3, i)-sign(A(4,3))*X(4, i))^(1/m)+...eta*A(4,5)* sign(X(5, i)-sign(A(4,5))*X(4, i))*abs(X(5, i)-sign(A(4,5))*X(4, i))^(1/m);U(5, i) = mu*A(5,4)* sign(X(4, i)-sign(A(5,4))*X(5, i))*abs(X(4, i)-sign(A(5,4))*X(5, i))^(2-1/m)+...mu*A(5,6)* sign(X(6, i)-sign(A(5,6))*X(5, i))*abs(X(6, i)-sign(A(5,6))*X(5, i))^(2-1/m)+...eta*A(5,4)* sign(X(4, i)-sign(A(5,4))*X(5, i))*abs(X(4, i)-sign(A(5,4))*X(5, i))^(1/m)+...eta*A(5,6)* sign(X(6, i)-sign(A(5,6))*X(5, i))*abs(X(6, i)-sign(A(5,6))*X(5, i))^(1/m); U(6, i) = mu*A(6,1)* sign(X(1, i)-sign(A(6,1))*X(6, i))*abs(X(1, i)-sign(A(6,1))*X(6, i))^(2-1/m)+...mu*A(6,5)* sign(X(5, i)-sign(A(6,5))*X(6, i))*abs(X(5, i)-sign(A(6,5))*X(6, i))^(2-1/m)+...eta*A(6,1)* sign(X(1, i)-sign(A(6,1))*X(6, i))*abs(X(1, i)-sign(A(6,1))*X(6, i))^(1/m)+...eta*A(6,5)* sign(X(5, i)-sign(A(6,5))*X(6, i))*abs(X(5, i)-sign(A(6,5))*X(6, i))^(1/m);X(:,i+1) = X(:,i) + U(:,i)*dT;end%% 绘图
subplot(1,1,1)
plot(t,X(1,:),'k','linewidth',2.0); hold on % x1
plot(t,X(2,:),'b','linewidth',2.0); hold on % x2
plot(t,X(3,:),'g','linewidth',2.0); hold on % x3
plot(t,X(4,:),'y','linewidth',2.0); hold on % x4
plot(t,X(5,:),'c','linewidth',2.0); hold on % x5
plot(t,X(6,:),'r','linewidth',2.0); hold on % x5
title('Position Trajectory');
legend("x_1", "x_2", "x_3", "x_4", "x_5", "x_6");
%axis([0 8 -8 8]); 
grid on; box on;