总结
非确定二部图上的蝴蝶结构统计,精确算法。在普通的蝴蝶结构统计上,增加了边权重,使得传统算法失效,再在这基础上定义新的统计并优化老方法。
动机
Butterfly的数量直接展示了二部图的密度,是个很重要的属性。相比于certain bipartite graph, uncertain bipartite graph 的边上多了权重,用来表示联系的概率。这种图会比一般的图更有表现能力,但现在少有这种图上的butterfly counting算法。
Butterfly counting使用案例
- Host-Parasite Network: 这种网络用来寻找寄生虫寄生于哪些宿主身上。此时二部图上的权重用来表示被感染的机率。通过butterfly counting可以对潜在的感染率和传播造成的影响进行评估。
- 推荐系统。此时二部图上的权重用来表示用户对某商品的喜好程度/购买可能。通过butterfly counting可以对不同推荐系统得到的推荐结果进行对比,越稠密的越好。
问题定义
和一般的butterfly counting不同,这里因为引入了uncertain属性,所以需要对概率设定一个阈值。
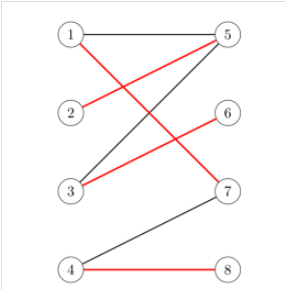
比如:
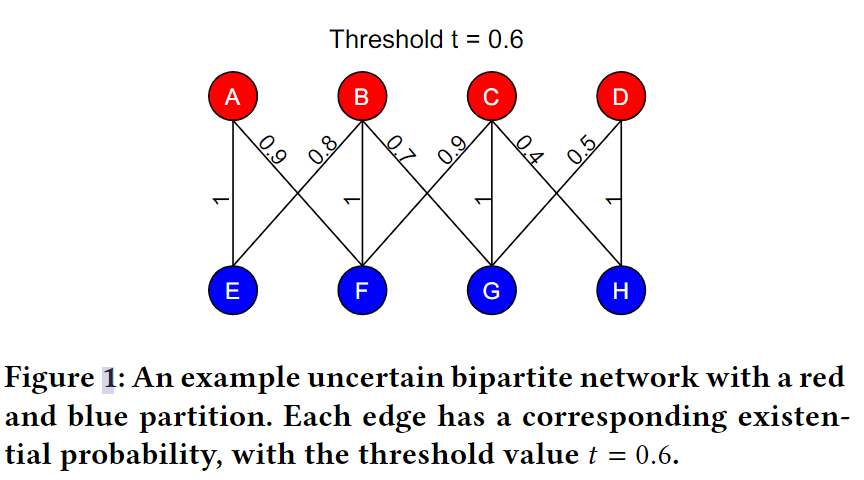
这张图里,阈值为0.6。而蝴蝶结构 B ( A , B , C , D ) B(A, B, C, D) B(A,B,C,D)的权重是 1 × 1 × 0.9 × 0.8 = 0.72 1 \times 1 \times 0.9 \times 0.8 = 0.72 1×1×0.9×0.8=0.72是满足的,但 B ( C , D , G , H ) B(C, D, G, H) B(C,D,G,H)则是 1 × 1 × 0.4 × 0.5 = 0.2 1 \times 1 \times 0.4 \times 0.5 = 0.2 1×1×0.4×0.5=0.2则是不满足的。用下面的定义来表示就是 P r ( B t ) ≥ 1 Pr(B_t) \geq 1 Pr(Bt)≥1。
计算剩下的可以得到,这张图的count是0.2。
顺便提一句,下面还有个wedge ∠ ( u , v , w ) , P r ( ∠ t ) ≥ t ∈ [ 0 , 1 ] \angle(u,v,w), Pr(\angle_t)\geq t \in [0,1] ∠(u,v,w),Pr(∠t)≥t∈[0,1]。同样的,满足条件的才会被视作图中的wedge。
很明显,已有的工作没法在这定义上实现counting。
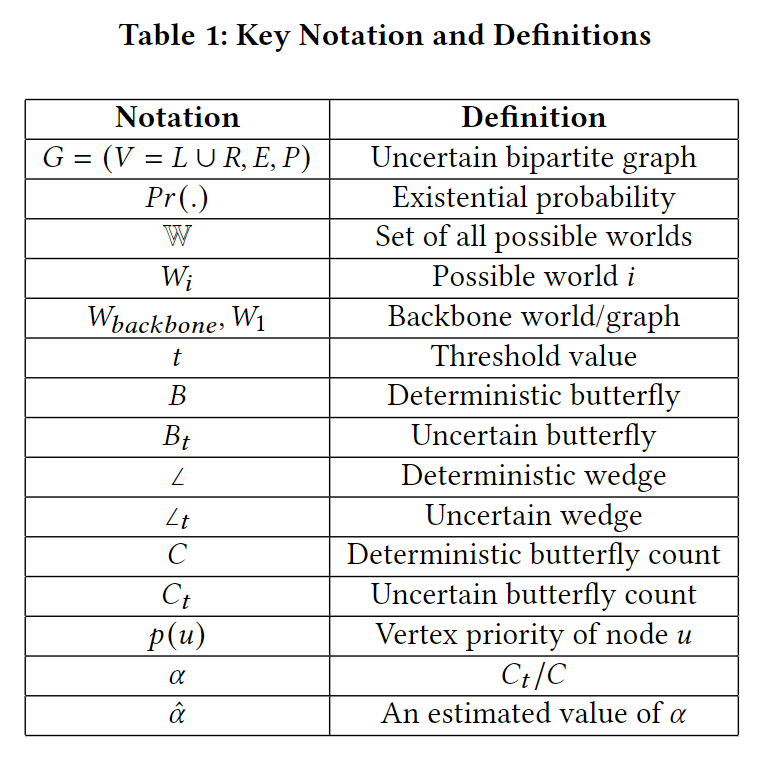
其中 P r ( e u , v ) ∈ ( 0 , 1 ] Pr(e_{u,v}) \in (0,1] Pr(eu,v)∈(0,1]
对于每个G的每套权重边(子图),都有一个possible world W i = ( V , E W i ) W_i=(V, E_{W_i}) Wi=(V,EWi)。以下式子本质就是出现这个概率世界的概率:
P r ( W i ) = ∏ e ∈ E W i P r ( e ) ⋅ ∏ e ∈ E \ E W i ( 1 − P r ( e ) ) Pr(W_i)=\prod_{e \in E_{W_i}} Pr(e) \cdot \prod_{e \in E\backslash E_{W_i}}(1-Pr(e)) Pr(Wi)=∏e∈EWiPr(e)⋅∏e∈E\EWi(1−Pr(e))
也就是说,当出现了某个具体的概率世界时,其实就是概率的不确定边转变为了实际发生的确定边。
对于每个G,都会有 2 ∣ E ∣ 2^{|E|} 2∣E∣个概率世界。看来是全包和一个都没有都算在内的。 W = { W 1 , … W 2 ∣ E ∣ } \mathbb{W}=\{W_1, \dots W_{2^{|E|}}\} W={W1,…W2∣E∣}。
E E E条边可以有 2 ∣ E ∣ 2^{|E|} 2∣E∣种子集的证明,可以认为每条边有在和不在两种情况,自然就是边数个2相乘。
Naive算法
首先有个顶点优先级定义:
if((deg(u) > deg(v)) or (deg(u) == deg(v) and id(u) > id(v))):p(u) > p(v)
利用优先级可以避免一个点被计算多次。

- 提取出一个概率世界
- 找出u为起点,优先级都低于u的u邻居v,以及wedge邻居w,把中间节点v存入H(w)
- 对于至少有2个v的w,判断这个蝴蝶符不符合要求,符合数量+1。
从度小的子图开始往上地毯式搜索。
提升算法

l中存了所有边从小到大的权重,然后对所有边做遍历
两边权重乘积小于t的肯定就出局了,顺便可以确定当前边需要配合的另一条边的最小权重,再去找有没有符合的,没有就直接跳过这条边,有就计数。
最终算法

概率低于t的点肯定不是,可以直接去掉,后面的基本和UBFC保持一致,不过存的是wedge,之后可以直接用wedge去统计数量。
![二分匹配大总结——Bipartite Graph Matchings[LnJJF]](https://img-blog.csdnimg.cn/f12f5708538c44c08101ac60cf3d8342.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBATG5KSkY=,size_20,color_FFFFFF,t_70,g_se,x_16)