Hu, A., Park, J.H., Cao, J. et al. Event-triggered bipartite consensus over cooperation-competition networks under DoS attacks. Sci. China Technol. Sci. 64, 157–168 (2021).
文章目录
- 1 Introduction
- 2 Problem description and preliminaries
- 2.1 Multiagent modeling and signed graph
- 2.2 Event-triggered bipartite consensus
- 2.3 DoS attack
- 2.4 Preliminaries
- 3. Main
- 3.1 Event-triggered scheme under DoS attacks
- 4. Numerical simulations
1 Introduction
2 Problem description and preliminaries
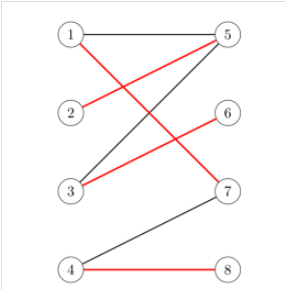
2.1 Multiagent modeling and signed graph
x ˙ i ( t ) = u i ( t ) (1) \dot{x}_i(t) = u_i(t) \tag{1} x˙i(t)=ui(t)(1)
2.2 Event-triggered bipartite consensus
连续时间的一致性控制协议:
u i ( t ) = ∑ j ∈ N i ∣ a i j ∣ ( sgn ( a i j ) x j ( t ) − x i ( t ) ) (2) u_i(t) = \sum_{j \in N_i} |a_{ij}| (\text{sgn}(a_{ij}) ~ x_j(t) - x_i(t)) \tag{2} ui(t)=j∈Ni∑∣aij∣(sgn(aij) xj(t)−xi(t))(2)
基于事件触发机制下,连续时间的一致性控制协议:
u i ( t ) = ∑ j ∈ N i ∣ a i j ∣ ( sgn ( a i j ) x ^ j ( t ) − x ^ i ( t ) ) (3) u_i(t) = \sum_{j \in N_i} |a_{ij}| (\text{sgn}(a_{ij}) ~ \red{\hat{x}_j(t)} - \red{\hat{x}_i(t)} ) \tag{3} ui(t)=j∈Ni∑∣aij∣(sgn(aij) x^j(t)−x^i(t))(3)
事件触发的状态值
x ^ i ( t ) = x i ( t k i ) \hat{x}_i(t) = x_i(\red{t_k^i}) x^i(t)=xi(tki)
x ^ j ( t ) = x j ( t k ′ j ) \hat{x}_j(t) = x_j(\red{t_{k'}^j}) x^j(t)=xj(tk′j)
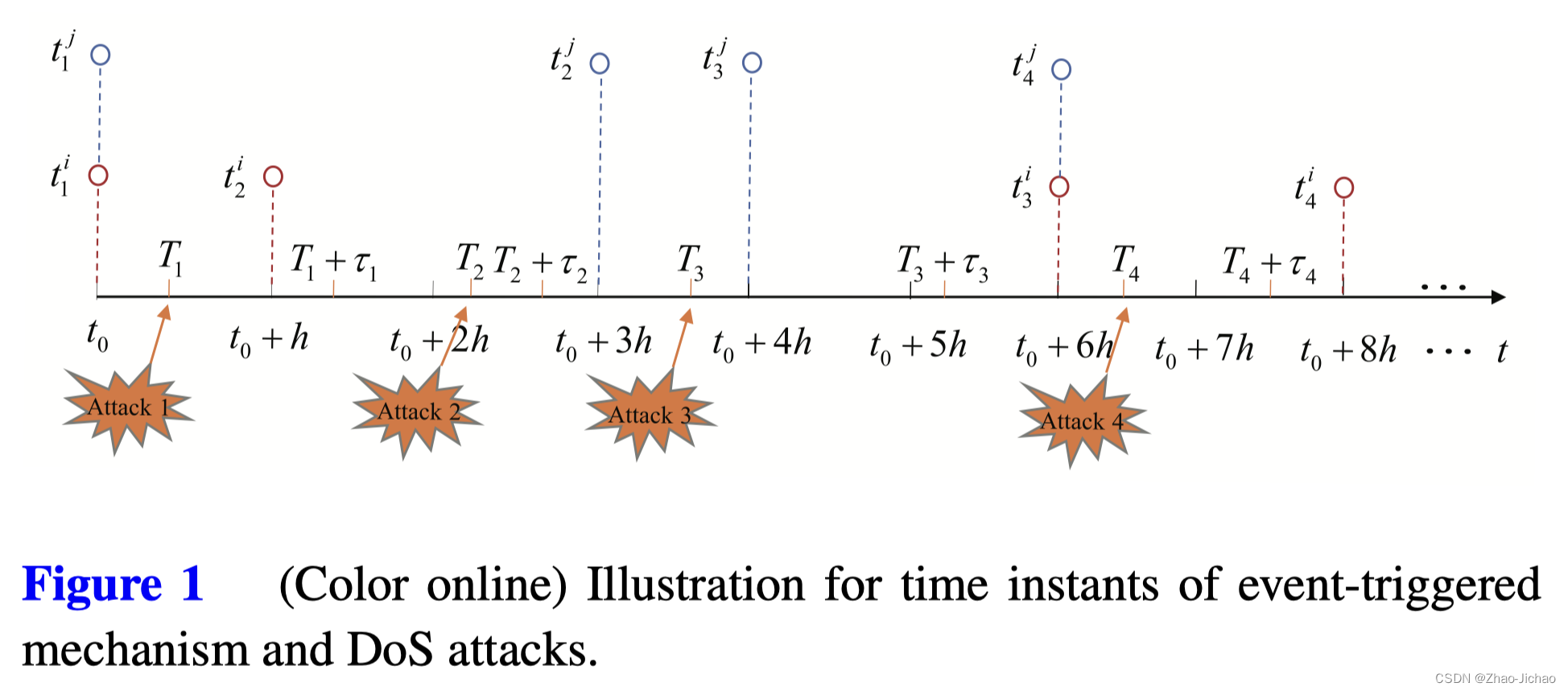
事件触发时刻用 t p i t_p^i tpi 表示
t k i = max t p i { t p i ≤ t , p = 1 , 2 , ⋯ } t_k^i = \max_{t_p^i} \{ t_p^i \le t, p = 1,2,\cdots \} tki=maxtpi{tpi≤t,p=1,2,⋯}
t k ′ j = max t p j { t p j ≤ t , p = 1 , 2 , ⋯ } t_{k'}^j = \max_{t_p^j} \{ t_p^j \le t, p = 1,2,\cdots \} tk′j=maxtpj{tpj≤t,p=1,2,⋯}
2.3 DoS attack
T q T_q Tq 表示攻击开始时间
τ q \tau_q τq 表示攻击持续时间
[ T q , T q + τ q ] [T_q, T_q + \tau_q] [Tq,Tq+τq] 时间段内无信息交换
Δ a ( t 0 , t ) \Delta^a(t_0,t) Δa(t0,t) 表示在时间段 [ t 0 , t ] [t_0, t] [t0,t] 内不能交换信息的总时间
Δ s ( t 0 , t ) \Delta^s(t_0,t) Δs(t0,t) 表示在时间段 [ t 0 , t ] [t_0, t] [t0,t] 内能交换信息的总时间
2.4 Preliminaries
3. Main
3.1 Event-triggered scheme under DoS attacks
采样周期 h > 0 h>0 h>0
t p + 1 i = min μ = 1 , 2 , ⋯ { t p i + μ h ∣ f i ( t p i + μ h ) > 0 } (8) t^i_{p+1} = \min_{\mu=1,2,\cdots} \{ t_p^i + \mu h ~|~ f_i(t_p^i + \mu h) > 0 \} \tag{8} tp+1i=μ=1,2,⋯min{tpi+μh ∣ fi(tpi+μh)>0}(8)
其中 f i ( t p i + μ h ) f_i(t_p^i + \mu h) fi(tpi+μh) 是一个关于误差的函数。
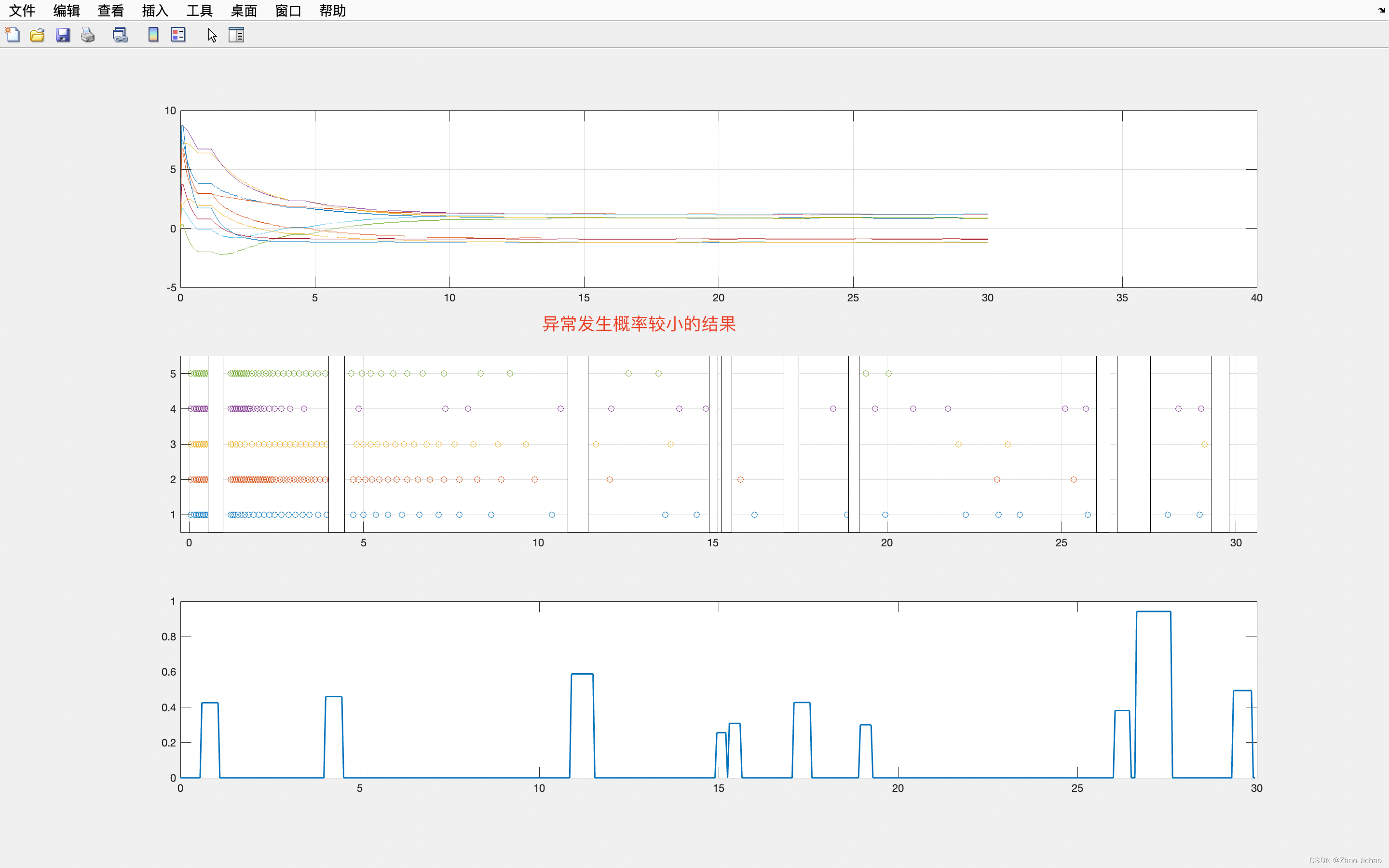
4. Numerical simulations
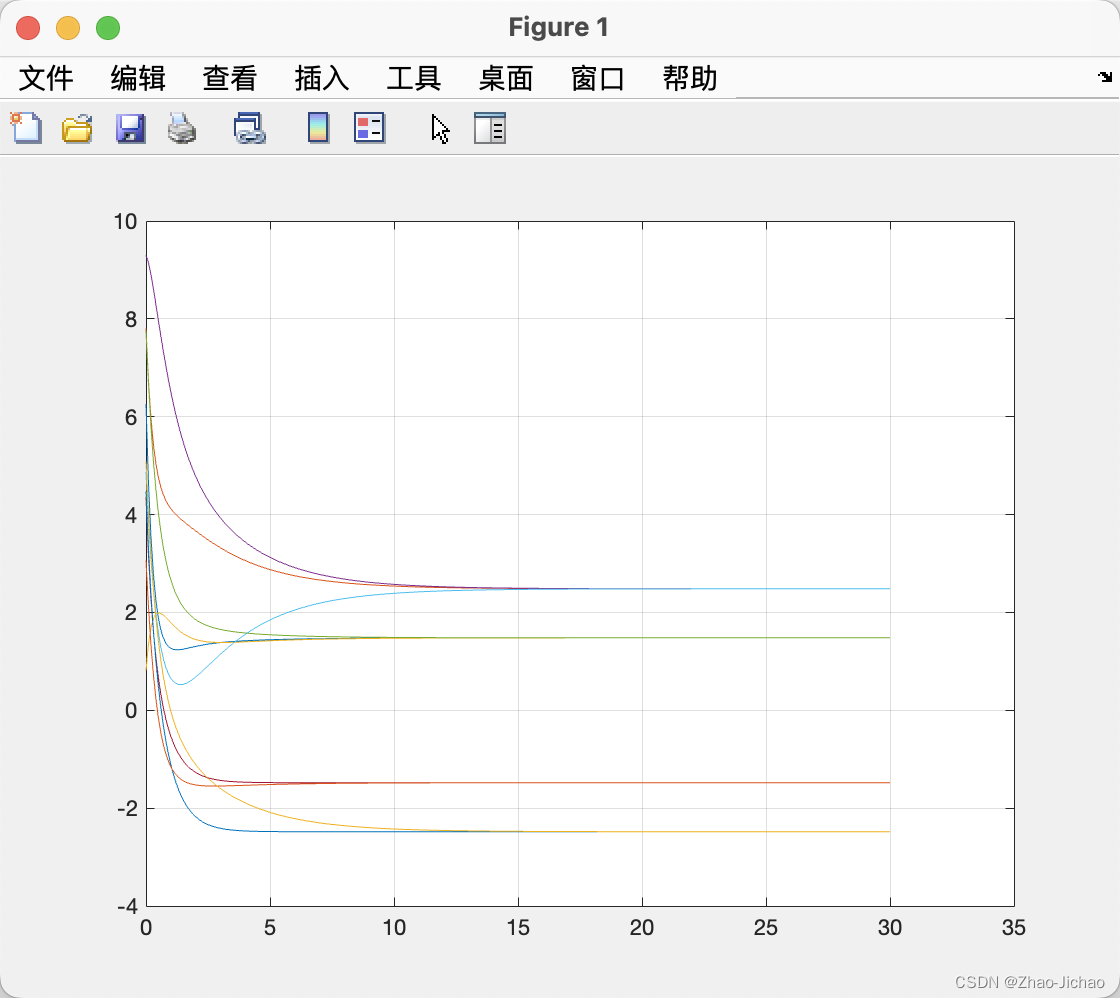
程序 Main_2020.m 的结果:
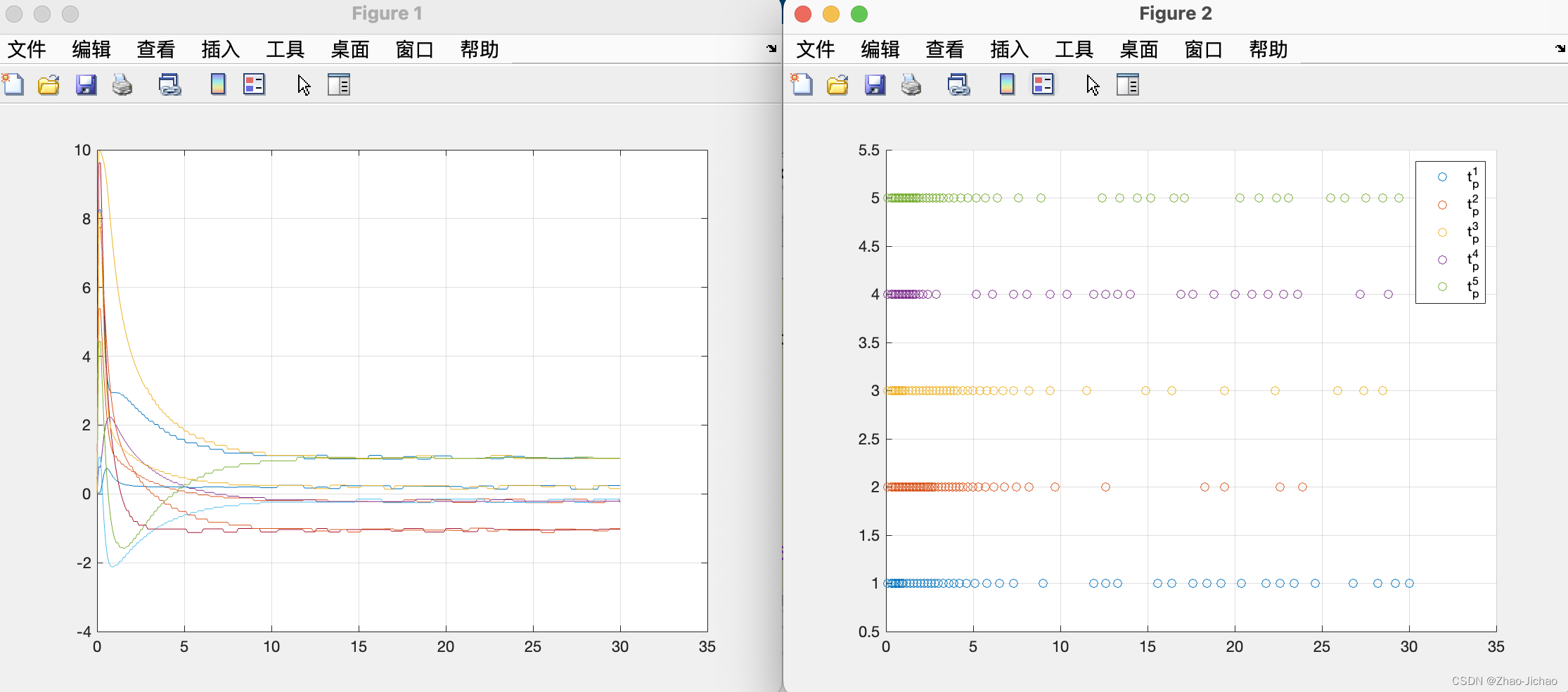
加入事件触发机制 Main_2020_ETC.m:
自己改的 DoS Main_2020_ETC_DoS.m:
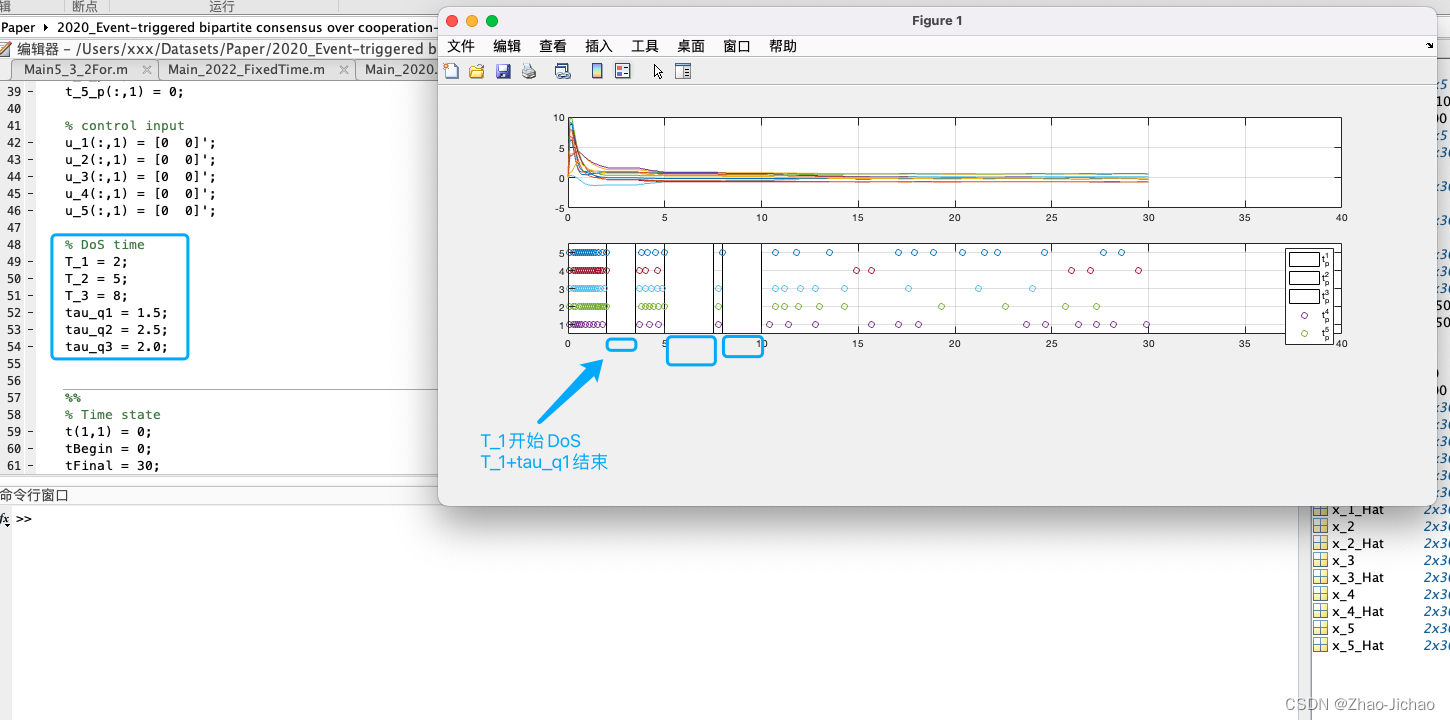
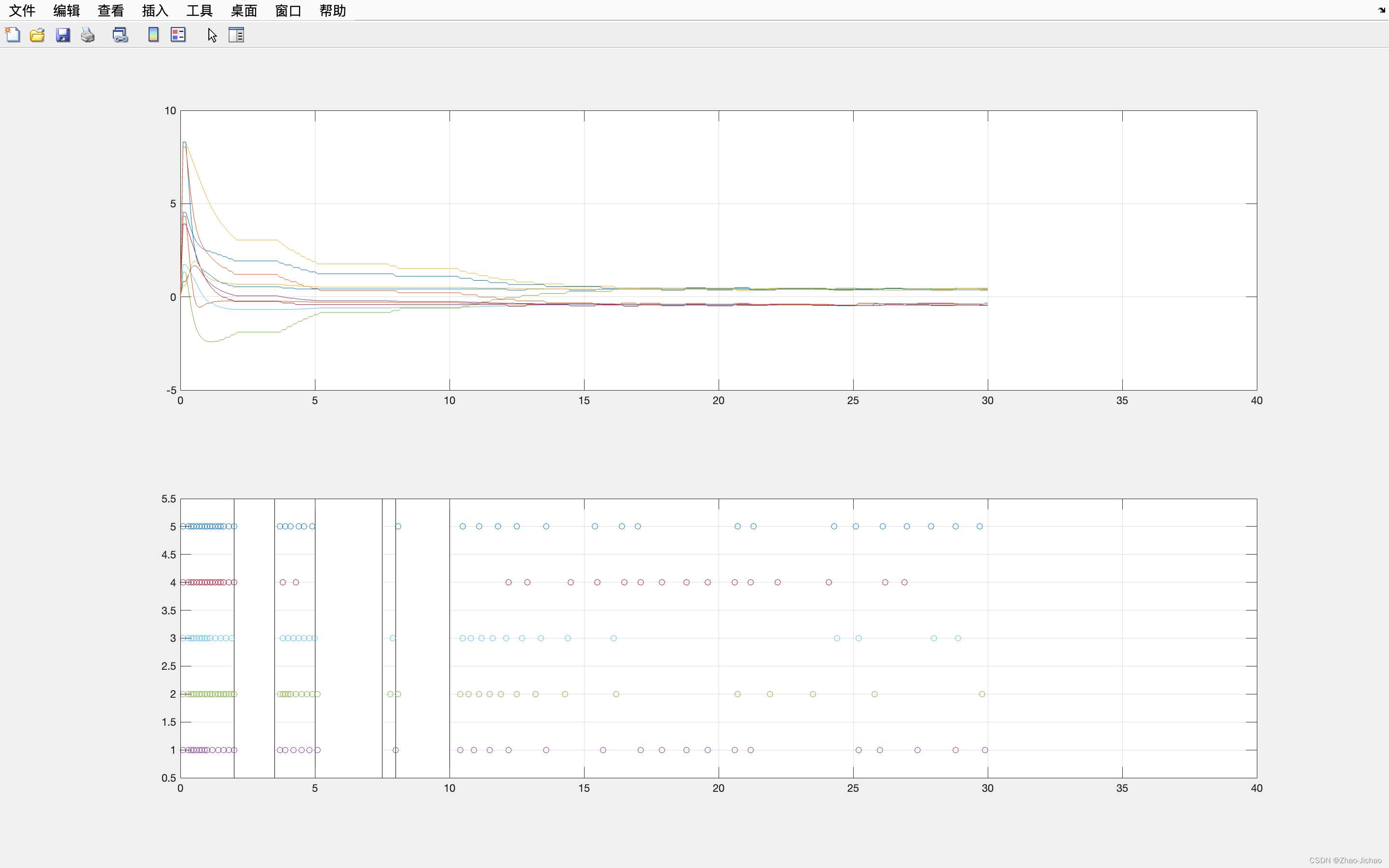
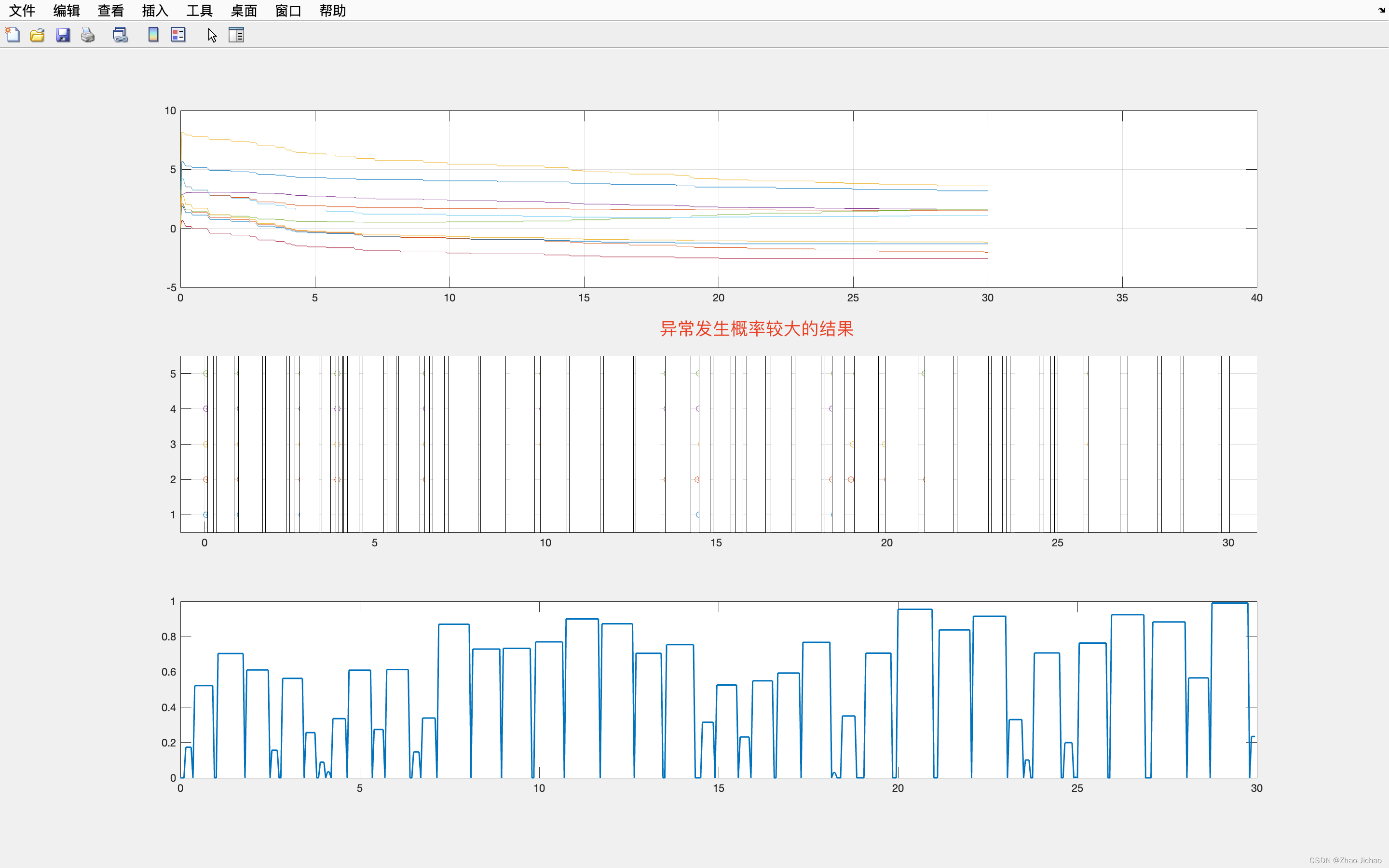
在之前工作的基础上,又修改了 DoS 的触发条件,改成了概率触发,对应程序 Main_2020_ETC_DoS2.m