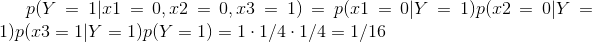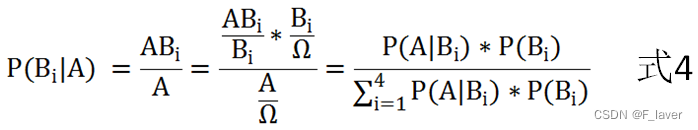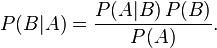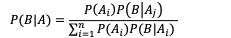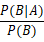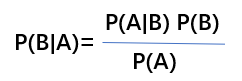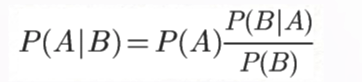基础知识：

①条件概率 ：P(B|A) = P(AB) / P(A)       其中P(AB) = P(A∩B) 即事件A 和事件B同时发生的概率

 由上式变形可知  P(AB) = P(A) *  P(B|A)。

②全概率公式 ： 在计算一个比较复杂事件的概率时，我们总是希望从已知的简单地事件的概率来计算，为此经常把一个复杂事件分解为若干个不相容的简单事件的和，再分别计算这些简单事件的概率，最后利用有限可加性得到较复杂事件的概率。

设A1,A2,A3,···,An是样本空间Ω的一个划分（A1-An中 每次实验有且仅有一个发生）B是任意一个事件，则 全概率公式的表达形式： 

③先验概率/后验概率：

后验概率  是   由果推因 你知道是这个结果 那么造成这个结果的原因的概率是多少呢？

 似然概率 是   由因推果   哪个原因最有可能导致这个结果的概率。 

贝叶斯公式：

贝叶斯公式是求解后验概率的一种方法：

贝叶斯公式内容 :      

证明：

其中P(B|Ai)   叫做似然概率 他一般代表观测的准确性  。

       比如用体重计测量体重  P(A1 = 100) 表示重量为100kg的估计概率 ， P(A2 = 101)表示总量为101kg的概率  。实际的体重在测量时 B = 100.5，但是这个测量值也是有误差的，并不是真实值。那么 P(B|A1)的含义就是当真实体重为100.5kg时，体重计测得体重为100kg的概率是多少。

       后验概率 所有的 值加起来概率和为1，这个可以通过全概率公式很好的算出来，但是似然概率之间的大小并没有影响。