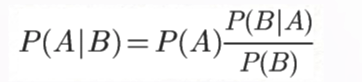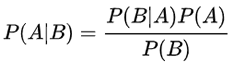从贝叶斯定理说开去
简介
贝叶斯定理是18世纪英国数学家托马斯·贝叶斯(Thomas Bayes)提出得重要概率论理论。以下摘一段 wikipedia 上的简介:
所谓的贝叶斯定理源于他生前为解决一个“逆概”问题写的一篇文章,而这篇文章是在他死后才由他的一位朋友发表出来的。在贝叶斯写这篇文章之前,人们已经能够计算“正向概率”,如“假设袋子里面有 N 个白球,M 个黑球,你伸手进去摸一把,摸出黑球的概率是多大”。而一个自然而然的问题是反过来:“如果我们事先并不知道袋子里面黑白球的比例,而是闭着眼睛摸出一个(或好几个)球,观察这些取出来的球的颜色之后,那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。这个问题,就是所谓的逆向概率问题。
贝叶斯定理的思想出现在18世纪,但真正大规模派上用途还得等到计算机的出现。因为这个定理需要大规模的数据计算推理才能凸显效果,它在很多计算机应用领域中都大有作为,如自然语言处理,机器学习,推荐系统,图像识别,博弈论等等。
定义
贝叶斯定理是关于随机事件 A 和 B 的条件概率:
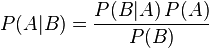
其中P(A|B)是在 B 发生的情况下 A 发生的可能性。
在贝叶斯定理中,每个名词都有约定俗成的名称:
P(A)是 A 的先验概率,之所以称为“先验”是因为它不考虑任何 B 方面的因素。
P(A|B)是已知 B 发生后 A 的条件概率,也由于得自 B 的取值而被称作 A 的后验概率。
P(B|A)是已知 A 发生后 B 的条件概率,也由于得自 A 的取值而被称作 B 的后验概率。
P(B)是 B 的先验概率,也作标淮化常量(normalizing constant)。
按这些术语,贝叶斯定理可表述为:
后验概率 = (相似度 * 先验概率)/标淮化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
另外,比例P(B|A)/P(B)也有时被称作标淮相似度(standardised likelihood),Bayes定理可表述为:
后验概率 = 标淮相似度 * 先验概率
条件概率就是事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在 B 发生的条件下 A 发生的概率”。
联合概率表示两个事件共同发生(数学概念上的交集)的概率。A 与 B 的联合概率表示为 。
。
推导
我们可以从条件概率的定义推导出贝叶斯定理。
根据条件概率的定义,在事件 B 发生的条件下事件 A 发生的概率为:
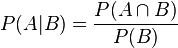
同样地,在事件 A 发生的条件下事件 B 发生的概率为:
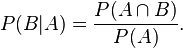
结合这两个方程式,我们可以得到:
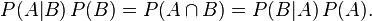
这个引理有时称作概率乘法规则。上式两边同除以 P(A),若P(A)是非零的,我们可以得到贝叶斯定理:
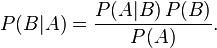
解释
通常,事件 A 在事件 B 发生的条件下的概率,与事件 B 在事件 A 发生的条件下的概率是不一样的;然而,这两者是有确定关系的,贝叶斯定理就是这种关系的陈述。
贝叶斯公式的用途在于通过己知三个概率来推测第四个概率。它的内容是:在 B 出现的前提下,A 出现的概率等于 A 出现的前提下 B 出现的概率乘以 A 出现的概率再除以 B 出现的概率。通过联系 A 与 B,计算从一个事件发生的情况下另一事件发生的概率,即从结果上溯到源头(也即逆向概率)。
通俗地讲就是当你不能确定某一个事件发生的概率时,你可以依靠与该事件本质属性相关的事件发生的概率去推测该事件发生的概率。用数学语言表达就是:支持某项属性的事件发生得愈多,则该事件发生的的可能性就愈大。这个推理过程有时候也叫贝叶斯推理。
示例
示例一:应当根据新情况更新先验概率
《决策与判断》第十二章中讲到人们都有保守主义情结,即使出现了新信息,也不愿意根据新信息来更新先验概率。用前面解释里面的话说就是:新信息是 B 事件不断发生,人们本应该根据这个信息去更新 A 事件发生的概率,但人们却更愿意固守之前估计的 A 事件发生的概率。
书中举了这样一个调查案例:
假设有两个各装了100个球的箱子,甲箱子中有70个红球,30个绿球,乙箱子中有30个红球,70个绿球。假设随机选择其中一个箱子,从中拿出一个球记下球色再放回原箱子,如此重复12次,记录得到8次红球,4次绿球。问题来了,你认为被选择的箱子是甲箱子的概率有多大?
调查结果显示,大部分人都低估了选择的是甲箱子的概率。根据贝叶斯定理,正确答案是96.7%。下面容我来详细分析解答。
刚开始选择甲乙两箱子的先验概率都是50%,因为是随机二选一(这是贝叶斯定理二选一的特殊形式)。即有:
P(甲) = 0.5, P(乙) = 1 - P(甲);
这时在拿出一个球是红球的情况下,我们就应该根据这个信息来更新选择的是甲箱子的先验概率:
P(甲|红球1) = P(红球|甲) × P(甲) / (P(红球|甲) × P(甲) + (P(红球|乙) × P(乙)))
P(红球|甲):甲箱子中拿到红球的概率
P(红球|乙):乙箱子中拿到红球的概率
因此在出现一个红球的情况下,选择的是甲箱子的先验概率就可被修正为:
P(甲|红球1) = 0.7 × 0.5 / (0.7 × 0.5 + 0.3 × 0.5) = 0.7
即在出现一个红球之后,甲乙箱子被选中的先验概率就被修正为:
P(甲) = 0.7, P(乙) = 1 - P(甲) = 0.3;
如此重复,直到经历8次红球修正(概率增加),4此绿球修正(概率减少)之后,选择的是甲箱子的概率为:96.7%。
我写了一段 Python 代码来解这个问题:
<figure class="code" style="margin: 0px 0px 1.5em; padding: 0px; border: 0px; font-family: 'PT Serif', Georgia, Times, 'Times New Roman', serif; font-stretch: inherit; line-height: 27.5999984741211px; font-size: 18px; vertical-align: baseline; -webkit-box-shadow: rgba(0, 0, 0, 0.0588235) 0px 0px 10px; box-shadow: rgba(0, 0, 0, 0.0588235) 0px 0px 10px; color: rgb(34, 34, 34); background: none rgb(248, 248, 248);