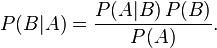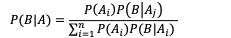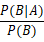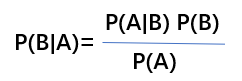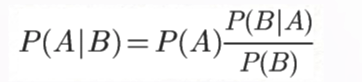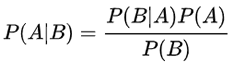朴素贝叶斯是一种基于贝叶斯定理的简单概率分类器（分类又被称为监督式学习，所谓监督式学习即从已知样本数据中的特征信息去推测可能出现的输出以完成分类，反之聚类问题被称为非监督式学习），朴素贝叶斯在处理文本数据时可以得到较好的分类结果，所以它被广泛应用于文本分类/垃圾邮件过滤/自然语言处理等场景。

了解贝叶斯定理前，我们需要先了解条件概率与全概率公式。

条件概率（Conditional Probability）是指在事件B发生的情况下，事件A发生的概率，用P(A|B)表示，读作在B条件下的A的概率。

我们可以很清楚看到，在事件B发生的概率下，事件A发生的概率为：

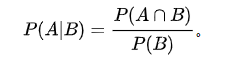
同样地，在事件A发生的条件下事件B发生的概率

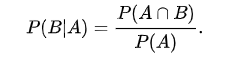
将两个式子合并，得到：

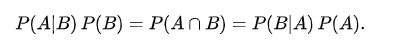
两边同时除以非0的P(B)，得到贝叶斯定理

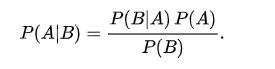
在贝叶斯定理中，每个名词都有约定俗成的名称：

• P(A|B)是已知B发生后，A的条件概率，也由于得自B的取值而被称作A的后验概率。

• P(A)是A的先验概率（或边缘概率）。之所以称为"先验"是因为它不考虑任何B方面的因素。

• P(B|A)是已知A发生后，B的条件概率。也由于得自A的取值而被称作B的后验概率。

• P(B)是B的先验概率。

P(B|A) / P(B)也有时被称作标准似然度（standardised likelihood），贝叶斯定理可表述为：

后验概率 = 标准似然度*先验概率

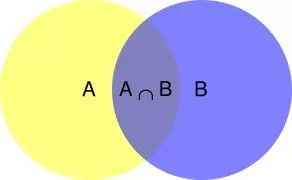
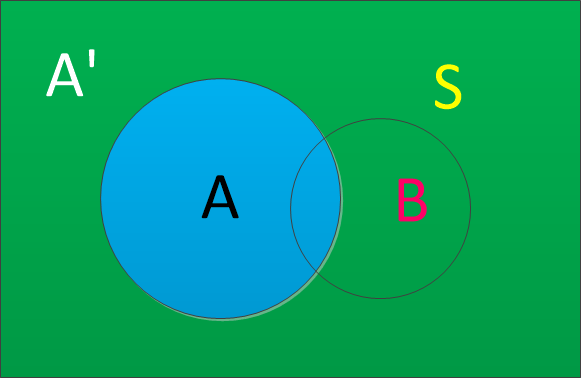
假定样本空间S，是两个事件A与A'的和。

蓝色部分为A，绿色为A'，即A的补集，他们共同构成了样本空间S。

那么，对于事件B，可以看成2部分，P(AB)与P(A'B)。

即

由条件概率可知，

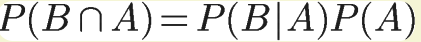
那么，有全概率公式。

一所学校里面有 60% 的男生，40% 的女生。男生总是穿长裤，女生则一半穿长裤一半穿裙子。有了这些信息之后我们可以容易地计算“随机选取一个学生，他（她）穿长裤的概率和穿裙子的概率是多大”，这个就是前面说的“正向概率”的计算。然而，假设你走在校园中，迎面走来一个穿长裤的学生（很不幸的是你高度近似，你只看得见他（她）穿的是否长裤，而无法确定他（她）的性别），你能够推断出他（她）是男生的概率是多大吗？

记长裤为事件A，短裤为事件B，男生为事件M，女生为F，那么我们需要求P(M | A)，由贝叶斯公式有：

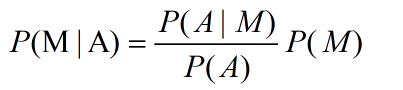
由全概率公式有：

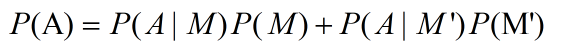
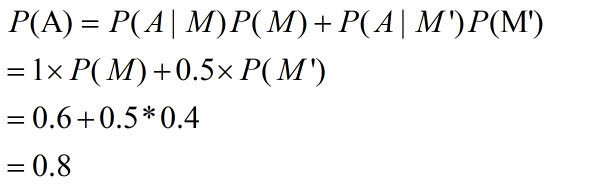
那么

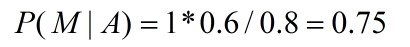
可以看到，本来，男生都穿长裤，概率是0.6，在知道穿长裤的条件下，是男生的后验概率就增加了为0.75。

吸毒者检测

下面展示贝叶斯定理在检测吸毒者时的应用。假设一个常规的检测结果的灵敏度和特异度均为99%，即吸毒者每次检测呈阳性（+）的概率为99%。而不吸毒者每次检测呈阴性（-）的概率为99%。从检测结果的概率来看，检测结果是比较准确的，但是贝叶斯定理却可以揭示一个潜在的问题。假设某公司对全体雇员进行吸毒检测，已知0.5%的雇员吸毒。请问每位检测结果呈阳性的雇员吸毒的概率有多高？

胰腺癌检测

基于贝叶斯定理：即使100%的胰腺癌症患者都有某症状，而某人有同样的症状，绝对不代表该人有100%的概率得胰腺癌，还需要考虑先验概率，假设胰腺癌的发病率是十万分之一，而全球有同样症状的人有万分之一，则此人得胰腺癌的概率只有十分之一，90%的可能是是假阳性。

不良种子检测

基于贝叶斯定理：假设100%的不良种子都表现A性状，而种子表现A性状，并不代表此种子100%是不良种子，还需要考虑先验概率，假设一共有6万颗不良种子，在种子中的比例是十万分之一（假设总共有60亿颗种子），假设所有种子中有1/3表现A性状（即20亿颗种子表现A性状），则此种子为不良种子的概率只有十万分之三。

猜你喜欢