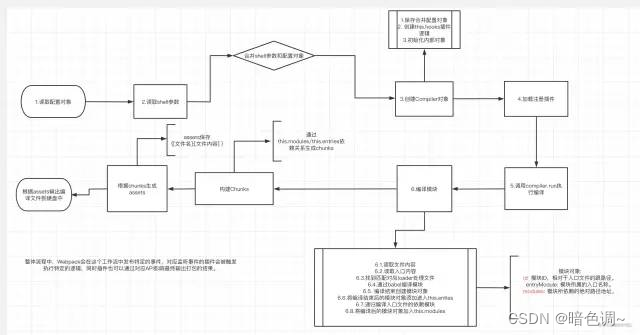
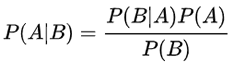小白之通俗易懂的贝叶斯定理
- 贝叶斯定理的产生以及意义
- 什么是贝叶斯定理?
- 贝叶斯定理的应用案例
- 贝叶斯定理套路
- 生活中的贝叶斯思维
转载自:https://mp.weixin.qq.com/s/lR3eeSWYHJDAJ9kJUzXc7w
贝叶斯定理的产生以及意义
1、贝叶斯定理的产生来源
- 英国数学家托马斯·贝叶斯(Thomas Bayes)在1763年发表的一篇论文中,首先提出了这个定理。而这篇论文是在他死后才由他的一位朋友发表出来的。在这篇论文中,他为了解决一个“逆向概率”问题,而提出了贝叶斯定理。
- 在贝叶斯写这篇文章之前,人们已经能够计算正向概率,比如杜蕾斯举办了一个抽奖,抽奖桶里有10个球,其中2个白球,8个黑球,抽到白球就算你中奖。你伸手进去随便摸出1颗球,摸出中奖球的概率是多大。根据频率概率的计算公式,你可以轻松的知道中奖的概率是2/10。
- 而贝叶斯在他的文章中是为了解决一个“逆概率”的问题。同样以抽奖为例,我们并不知道抽奖桶里有什么,而是摸出一个球,通过观察这个球的颜色,来预测这个桶里里白色球和黑色球的比例。
- 这个预测其实就可以用贝叶斯定理来做。贝叶斯当时的论文只是对“逆概率”这个问题的一个直接的求解尝试,这哥们当时并不清楚这里面这里面包含着的深刻思想。然而后来,贝叶斯定理席卷了概率论,并将应用延伸到各个问题领域。可以说,所有需要作出概率预测的地方都可以见到贝叶斯定理的影子,特别地,贝叶斯是机器学习的核心方法之一。
2、为什么贝叶斯定理在现实生活中这么有用呢?
- 这是因为现实生活中的问题,大部分都是像上面的逆概率问题。生活中绝大多数决策面临的信息都是不完全的,我们手中只有有限的信息。既然无法得到全面的信息,我们就应该在信息有限的情况下,尽可能做出一个最优的预测。
- 比如,天气预报说,明天降雨的概率是30%。这是什么意思呢?因为我们无法像计算频率概率那样,重复地把明天过上100次,然后计算出大约有30次会下雨,所以只能利用有限的信息(过去天气的测量数据),采用贝叶斯定理来预测出明天下雨的概率是多少。
- 同样的,在现实世界中,我们每个人都需要预测。要想深入分析未来、思考是否买股票、政策给自己带来哪些机遇、提出新产品构想,或者只是计划一周的饭菜。贝叶斯定理就是为了解决这些问题而诞生的,它可以根据过去的数据来预测出概率。贝叶斯定理的思考方式为我们提供了明显有效的方法来帮助我们提供能力,以便更好地预测未来的商业、金融、以及日常生活。
3、贝叶斯定理有什么用?在有限的信息下,能够帮助我们预测出概率。
什么是贝叶斯定理?
贝叶斯定理公式如下:
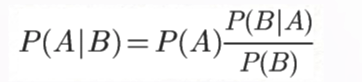
贝叶斯定理其实就是下面图片中的概率公式,这里先不讲这个公式,而是重点关注它的使用价值,因为只有理解了它的使用意义,你才会更有兴趣去学习它。其实,我和你一样,不喜欢公式。我们还是从一个例子开始聊起。
我的朋友小鹿说,他女神每次看到他的时候都会冲他笑,他想知道女神是不是喜欢他呢?谁让我学过统计概率知识呢,下面我们一起用贝叶斯帮小鹿预测以下女神喜欢他的概率有多大,这样小鹿就可以根据概率的大小来决定是否要表白女神。
首先,我们分析给定的已知信息和未知信息:
1)要求解的问题:女神喜欢你,记为A事件
2)已知条件:女神经常冲你笑,记为B事件
根据条件概率,P(A|B)是女神经常冲你笑这个B事件发生后女神喜欢你的概率(A事件)。
现在,我们来详细解释公式:
1)先验概率
我们把P(A)称为"先验概率"(Prior probability),即在不知道B事件发生的前提下,我们对A事件发生概率的一个主观判断。这个例子里就是在不知道女神经常对你笑的前提下,来主观判断出女神喜欢一个人的概率。这里我们假设是50%,也就是有可能喜欢你,也有可能不喜欢还你的概率各是一半。
2)可能性函数
P(B|A)/P(B)称为**“可能性函数”(Likelyhood),这是一个调整因子,即新信息事件B的发生调整,作用是,使得先验概率更接近真实概率。**
可能性函数你可以理解为新信息过来后,对先验概率的一个调整。比如上面的例子 在女神没有对笑之前,你觉得女神喜欢你的概率50%(先验概率/主管判断),女生经常对你笑(调整因子/新的信息),使得你觉得女神喜欢你的概率上升而超过50%(后验概率);又比如我们刚开始看到“人工智能”这个信息,你有自己的理解(先验概率/主观判断),但是当你学习了一些数据分析,或者看了些这方面的书后(新的信息),然后你根据掌握的最新信息优化了自己之前的理解(可能性函数/调整因子),最后重新理解了“人工智能”这个信息(后验概率)
如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;
如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;
如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
还是刚才的例子,根据女神经常冲你笑这个新的信息,我调查走访了女神的闺蜜,最后发现女神平日比较高冷,很少对人笑。所以我估计出"可能性函数"P(B|A)/P(B)=1.5(具体如何估计,省去1万字,后面会有更详细科学的例子)
3)后验概率
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。这个例子里就是在女神冲你笑后,对女神喜欢你的概率重新预测。
带入贝叶斯公式计算出P(A|B)=P(A)* P(B|A)/P(B)=50% *1.5=75%
因此,女神经常冲你笑,喜欢上你的概率是75%。这说明,女神经常冲你笑这个新信息的推断能力很强,将50%的"先验概率"一下子提高到了75%的"后验概率"。
现在我们再来看一遍贝叶斯公式,你现在就能明白这个公式背后的最关键思想了:
我们先根据以往的经验预估一个"先验概率"P(A),然后加入新的信息(实验结果B),这样有了新的信息后,我们对事件A的预测就更加准确。
因此,贝叶斯定理可以理解成下面的式子:
后验概率(新信息出现后A发生的概率)=先验概率(A发生的概率)x可能性函数(新信息带出现来的调整)
贝叶斯的底层思想就是:
如果我能掌握一个事情的全部信息,我当然能计算出一个客观概率(古典概率、正向概率)。可是生活中绝大多数决策面临的信息都是不全的,我们手中只有有限的信息。既然无法得到全面的信息,我们就在信息有限的情况下,尽可能做出一个好的预测。也就是,在主观判断的基础上,可以先估计一个值(先验概率),然后根据观察的新信息不断修正(可能性函数)。
贝叶斯定理的应用案例
案例1:贝叶斯定理在做判断上的应用
有两个一模一样的碗,1号碗里有30个巧克力和10个水果糖,2号碗里有20个巧克力和20个水果糖。然后把碗盖住。随机选择一个碗,从里面摸出一个巧克力。
问题:这颗巧克力来自1号碗的概率是多少?
好了,下面我就用套路来解决这个问题,到最后我会给出这个套路。
第1步,分解问题
1)要求解的问题:取出的巧克力,来自1号碗的概率是多少?
来自1号碗记为事件A1,来自2号碗记为事件A2
取出的是巧克力,记为事件B,
那么要求的问题就是P(A1|B),即取出的是巧克力,来自1号碗的概率
2)已知信息:
1号碗里有30个巧克力和10个水果糖
2号碗里有20个巧克力和20个水果糖
取出的是巧克力
第2步,应用贝叶斯定理
1)求先验概率
由于两个碗是一样的,所以在得到新信息(取出是巧克力之前),这两个碗被选中的概率相同,因此P(A1)=P(A2)=0.5,(其中A1表示来自1号碗,A2表示来自2号碗)
这个概率就是"先验概率",即没有做实验之前,来自一号碗、二号碗的概率都是0.5。
2)求可能性函数
P(B|A1)/P(B)
其中,P(B|A1)表示从一号碗中(A1)取出巧克力(B)的概率。因为1号碗里有10个水果糖和30个巧克力,所以P(B|A1)=30/(30+10)=75% 根据全概率公式,可以求得P(B)=P(B|A1)P(A1)+P(B|A2)P(A2)=62.5%
可能性函数P(B|A1)/P(B)=75%/62.5%=1.2 可能性函数>1.表示新信息B对事情A1的可能性增强了。
3)代入贝叶斯公式求后验概率
将上述计算结果,带入贝叶斯定理,即可算出P(A1|B)=60%
这个例子中我们需要关注的是约束条件:抓出的是巧克力。如果没有这个约束条件在,来自一号碗这件事的概率就是50%了,因为巧克力的分布不均把概率从50%提升到60%。
贝叶斯垃圾邮件过滤器
垃圾邮件是一种令人头痛的问题,困扰着所有的互联网用户。全球垃圾邮件的高峰出现在2006年,那时候所有邮件中90%都是垃圾,2015年6月份全球垃圾邮件的比例数字首次降低到50%以下。
最初的垃圾邮件过滤是靠静态关键词加一些判断条件来过滤,效果不好,漏网之鱼多,冤枉的也不少。
2002年,Paul Graham提出使用"贝叶斯推断"过滤垃圾邮件。他说,这样做的效果,好得不可思议。1000封垃圾邮件可以过滤掉995封,且没有一个误判。因为典型的垃圾邮件词汇在垃圾邮件中会以更高的频率出现,所以在做贝叶斯公式计算时,肯定会被识别出来。之后用最高频的15个垃圾词汇做联合概率计算,联合概率的结果超过90%将说明它是垃圾邮件。用贝叶斯过滤器可以识别很多改写过的垃圾邮件,而且错判率非常低。甚至不要求对初始值有多么精确,精度会在随后计算中逐渐逼近真实情况。
贝叶斯定理套路
贝叶斯定理应用的套路,你就更清楚了,会发现像小学生做应用题一样简单:
第1步. 分解问题
简单来说就像做应用题的感觉,先列出解决这个问题所需要的一些条件,然后记清楚哪些是已知的,哪些是未知的。
1)要求解的问题是什么?
识别出哪个是贝叶斯中的事件A(一般是想要知道的问题),哪个是事件B(一般是新的信息,或者实验结果)
2)已知条件是什么?
第2步.应用贝叶斯定理
第3步.求贝叶斯公式中的2个指标
1)求先验概率
2)求可能性函数
3)带入贝叶斯公式求后验概率
生活中的贝叶斯思维
贝叶斯定理与人脑的工作机制很像,这也是为什么它能成为机器学习的基础。
如果你仔细观察小孩学习新东西的这个能力,会发现,很多东西根本就是看一遍就会。比如我3岁的外甥,看了我做俯卧撑的动作,也做了一次这个动作,虽然动作不标准,但是也是有模有样。
同样的,我告诉他一个新单词,他一开始并不知道这个词是什么意思,但是他可以根据当时的情景,先来个猜测(先验概率/主观判断)。一有机会,他就会在不同的场合说出这个词,然后观察你的反应。如果我告诉他用对了,他就会进一步记住这个词的意思,如果我告诉他用错了,他就会进行相应调整。(可能性函数/调整因子)。经过这样反复的猜测、试探、调整主观判断,就是贝叶斯定理思维的过程。
同样的,我们成人也在用贝叶斯思维来做出决策。比如,你和女神在聊天的时候,如果对方说出“虽然”两个字,你大概就会猜测,对方后继九成的可能性会说出“但是”。我们的大脑看起来就好像是天生在用贝叶斯定理,即根据生活的经历有了主观判断(先验概率),然后根据搜集新的信息来修正(可能性函数/调整因子),最后做出高概率的预测(后验概率)。