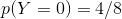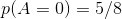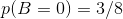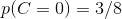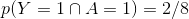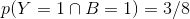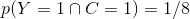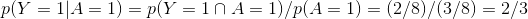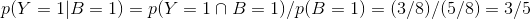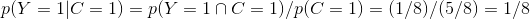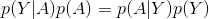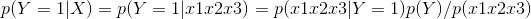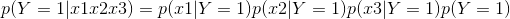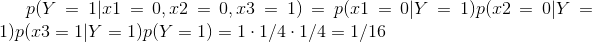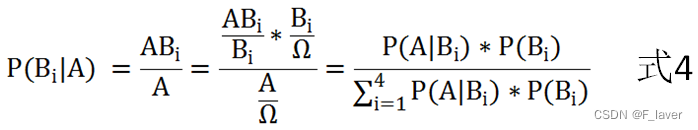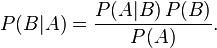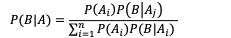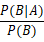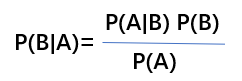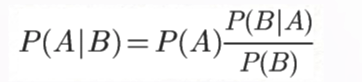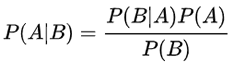贝叶斯公式
定理贝叶斯的英文概率论中的一个定理,跟它随机变量的条件概率以及边缘概率分布有关。
下面是贝叶斯的公式:
其中P(A | B)。是指在事件乙发生的情况下事件甲发生的概率其中甲代表的是所属的类别(Y),B代表的是特征(x)的
在贝叶斯定理中,每个名词都有约定俗成的名称:
- P(A | B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
- P(A)是A的先验概率(或边缘概率)。之所以称为“先验”是因为它不考虑任何B方面的因素。
- P(B | A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
- P(B)是B的先验概率或边缘概率。
下面我们举个例子来运用贝叶斯定理
这个表格是有关学生考试是否挂科的,1表示挂科,0表示没挂科,其他三个属性代表的是学生在考前所做过的事情,1表示做了,0表示没有做
| 是否挂科(Y) | 喝酒(A) | 打游戏(B) | 学习(C) |
| 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
通过这个表我们可以计算出我们所要得到的一些概率:
总共有8名学生的记录,其中挂科的总共有4名学生,所以我们可以算出:(有点多余啊,太简单了)
挂科的概率为 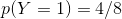
喝酒的概率为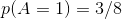
打游戏的概率为 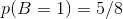
学习的概率为 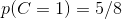
上面计算的只是某一个时间发生的概率,现在计算一下多件事同时发生的概率:
喝酒并且挂科的概率为
打游戏并且挂科的概率为
学习并且挂科的概率为
现在我们来计算一下当喝酒(A)时,挂科的概率
这个概率的表达式为
同理
当打游戏(B)时,挂科的概率
当学习(C)时,挂科的概率
通过公式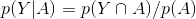
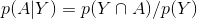
这样我们就可以得到 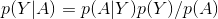
因为阿为特征,所以我们可以将阿用特征X代替,X为所有特征(X = X1,X2,X3,即为A,B,C)
由于在计算概率时,所有概率的分母都相同,所以在计算时就不需要考虑分母。并在朴素贝叶斯之所以朴素,原因就在于它认为各个特征值之间是相互独立的,因此可以简化为
通过知道X1,X2,X3的取值求得概率,就比如我们现在求一下表中第二条的概率,从表中可以知道X1 = 0,X2 = 0,X3 = 1,从前面所求的概率可以求到
通过这个概率可以知道当在考试前不喝酒,不打游戏,学习的话挂科的概率为1/16,所以说考试之间还是得学习的!
根据这个例子,相信大家可以很方便的理解贝叶斯公式。那么在理解完了贝叶斯公式之后,我们能用它来做什么呢?这个在下一篇中,我们就要讲讲如何利用贝叶斯公式来实现机器学习中的朴素贝叶斯算法了
用朴素贝叶斯进行文本分类:https://blog.csdn.net/qq_39187675/article/details/85139574
(如有错误,请指正)