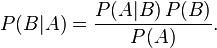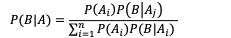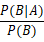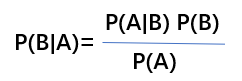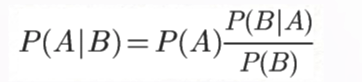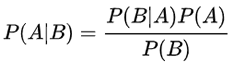[work*] 贝叶斯公式的通俗解释

本文节选自《人类最美的54个公式》转自量子位

我思故我在

引

我思故我在

AI背后的神秘公式

近代哲学奠基人，伟大的笛卡尔说出“我思故我在”时，上帝震惊了。

第一个被赋予公民身份的机器人Sophia（索菲娅）被问到：你怎么知道自己是机器人？Sophia的回答是：你怎么知道自己是人类？

机器人会反驳了，这到底是新世纪的福音，还是人类的转折？

AI（人工智能）已经不再是完全被动地向人类表述世界，而开始主观性地表达意见。

Google自动驾驶汽车的操纵系统，G-mail对垃圾邮件的处理，MIT主导的人类“写字”系统，以及最新的SIRI智能语音助手平台，还有挑战人类最后智慧堡垒的AlphaGo系统，都已经开始了“深度学习”暴风雨式革命。

这几年，机器智能向“我思故我在”这个哲学命题步步逼近，一只神秘之手躲在后面操纵，它就是贝叶斯公式。

当科学在证明自己对世界的客观认知时，贝叶斯公式却融入了人类的主观性。

“不科学”的贝叶斯-拉普拉斯公式

贝叶斯定理是18世纪英国数学家托马斯·贝叶斯提出的概率理论。

该定理源于他生前为解决一个“逆概”问题写的一篇文章，在贝叶斯写这篇文章之前，人们已经能够计算“正向概率”，如“假设袋子里面有P只螃蟹，Q只蜘蛛，你伸手进去摸一把，摸到螃蟹的概率是多大”。但反过来看：“如果我们事先并不知道袋子里面螃蟹和蜘蛛的比例，而是闭着眼睛摸出一只（或好几只）螃蟹，那么我们可以就此对袋子里面的螃蟹和蜘蛛的比例作出什么样的推测。”这个问题就是逆向概率问题。

这个研究看起来似乎简单而平淡无奇，直到他死后的两年才于1763年发表。它的数学原理很容易理解，就像一个迷信星座的HR，如果你碰到一个处女座的应聘者，你会推断那个人多半是一个追求完美的人。这就是说，当你不能准确知悉某个事物本质时，你可以依靠经验去判断其本质属性的概率。与其他统计学方法不同，贝叶斯方法建立在主观判断的基础上，让人感觉不科学，这也是它200多年来不为科学家们待见的原因。

除了贝叶斯，1774年，法国数学家拉普拉斯也非常“不科学”地发现了贝叶斯公式。这位创立了大名鼎鼎的谛听神兽拉普拉斯兽的科学家，给出了我们现在所用的贝叶斯公式的表达：

该公式表示在B事件发生的条件下A事件发生的条件概率，等于A事件发生条件下B事件发生的条件概率乘以A事件的概率，再除以B事件发生的概率。公式中，P(A）也叫做先验概率，P(A/B)叫做后验概率。

像微积分公式的全称是“牛顿-莱布尼茨公式”一样，贝叶斯公式至少应被称为“贝叶斯-拉普拉斯公式”才科学。

今天天气怎样？

贝叶斯公式是这样工作的

贝叶斯定理并不好懂，它到底是如何为人民服务的？

对于贝叶斯定理，参照上面的公式，首先要了解各个概率所对应的事件。

P(A|B)是在B发生的情况下A发生的概率；

P(A)是A发生的概率；

P(B|A)是在A发生的情况下B发生的概率；

P(B)是B发生的概率。

就知道你没看懂……那我还是举个经常用到的例子吧！

量子学派CEO良心发现放假10天，量子妹约定帅哥去爬梧桐山，希望玩到人约黄昏后占点便宜，然而天公不作美，一大早天空多云。

这可怎么办？60%的雨天的早上是多云的。帅哥说，不玩了吧。

量子妹当然不甘心，劝说帅哥：

1、多云不见得会下雨，大约30%日子早上是多云的！

2、深圳天气平均一个月才会3天下雨，10%的概率而已。

帅哥并不是绣花枕头，非常科学地用“贝叶斯公式”计算：

用“雨”来代表今天下雨，“云”来代表早上多云。

当早上多云时，当天会下雨的可能性是P(雨|云)。

P(雨|云) = P(雨)·P(云|雨) /P(云)

P(雨) 是今天下雨的概率 = 10%

P(云|雨) 是在下雨天早上有云的概率 = 60%

P(云) 早上多云的概率 = 30%

那么，贝叶斯定理的答案就出来了

P(雨|云) =0.1×0.6/0.3=0.20

帅哥毫无表情地说：今天下雨的概率是20%，可以去爬山。

量子妹看着美得不食人间烟火的帅哥，怯生生地问：你真的是人吗？

帅哥毫无表情地回答：我不是人，我是阿尔法狼。

贝叶斯公式如何逐步取得人类信任

今天的贝叶斯理论开始遍布一切。从物理学到癌症研究，从生态学到心理学。

物理学家提出了量子机器的贝叶斯解释，以及贝叶斯捍卫了弦和多重宇宙理论。

哲学家主张作为一个整体的科学可以被视为一个贝叶斯过程。

贝叶斯定理就快成像“热力学第二定律”一样放之四海皆准了。

特别是在IT界，AI大脑的思考和决策过程，被更多工程师设计成一个贝叶斯程序。

但贝叶斯诞生以来命途多舛，长期以来因为表面的不科学，并没有得到主流学界认可。

其实在日常生活中，我们也常使用贝叶斯公式进行决策。比如我们到河边钓鱼，根本就看不清楚河里哪里有鱼或者没鱼，似乎只能随机选择，但实际上我们会根据贝叶斯方法，利用以往积累经验找一个回水湾区开始垂钓。这就是我们根据先验知识进行主观判断，在钓过以后对这个地方有了更多了解，然后再进行选择。所以，在我们认识事物不全面的情况下，贝叶斯方法是一种非常理性且科学的方法。

贝叶斯公式得到主流科学界的认可，主要因为两件事：

1、《联邦党人文集》作者揭密

1788年，《联邦党人文集》匿名出版，作者汉密尔顿和麦迪逊写作风格几乎一致。两个人都逝世后，要找出每一篇文章的作者极其困难，哈佛大学通过对词汇的贝叶斯研究方法最终找出了每一篇的文章作者，研究方法在统计学界引发震动，被禁锢了200年的贝叶斯公式从魔盒里被释放出来。

2、美国天蝎号核潜艇搜救

1968年5月，美国海军天蝎号核潜艇在大西洋亚速海海域失踪。军方通过各种技术手段调查无果，最后不得不求助于数学家John Craven，John Craven提出的方案使用了贝叶斯公式，他召集了数学、潜艇、海事搜救等各个领域的专家，一边掷骰子一边通过贝叶斯公式一一排除小概率发生意外事故的搜索区域。

2014年初马航MH370航班失联后，科学家想到第一个方法就是利用贝叶斯定理开始区域搜索，这个时候，贝叶斯公式已经名满天下了。

语音识别

贝叶斯公式开始展示“神迹”

科大讯飞因为语音识别成为千亿级市值公司，首先得感谢贝叶斯公式和马尔科夫链。

自然语音处理一直是科学家面临的最大难题，在计算机语言处理领域，近几年引入了贝叶斯公式和马尔科夫链才有了长足进步（这里不详细介绍马尔科夫链）。

文字翻译尚可理解，但语音涉及各种动态语法，机器怎么知道你在说什么鸟语？

但当你在现场看到机器翻译的准确性，会感叹这简直就是“神迹”，比大部分现场翻译要强得多。

一旦出现条件概率，贝叶斯总能挺身而出。
我们用P(f|e)区别于以上的P(A|B)来解释语音识别功能。

统计机器翻译的问题可以描述为：给定一个句子e，它可能的外文翻译f中哪个是最靠谱的。即我们需要计算：P(f|e)。

P(f|e) ∝ P(f) * P(e|f)

这个式子的右端很容易解释：那些先验概率较高，并且更可能生成句子e的外文句子f将会胜出。我们只需简单统计就可以得出任意一个外文句子f的出现概率。然而 P(e|f)却不是那么好求的，给定一个候选的外文局子f，它生成（或对应）句子e的概率是多大？我们需要定义什么叫“对应”，这里需要用到一个分词对齐的平行语料库。

率先成功利用数学方法解决自然语言处理问题的是贾里尼克，他把语音识别简化为用贝叶斯公式处理的数学问题成功开辟了一条全新的问题解决路径。

随着大量数据输入模型进行迭代，随着计算能力的不断提高、大数据技术的发展，贝叶斯公式巨大的实用价值愈发体现出来。

语音识别仅仅只是贝叶斯公式运用的一个例子，其实贝叶斯定理的思想已经渗透到AI的方方面面。

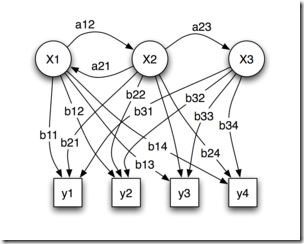
贝叶斯网络

AI智慧的“蜂群效应”

单个语音模型的建立让我们看到了贝叶斯定理解决问题的能力，但贝叶斯网络的拓展让我们隐约感觉到了AI背后“天网”的恐怖。

人类相对简单的问题已经解决得差不多了，剩下的都非常复杂。

龙卷风的形成，2的50次方可能的最小参数值比对。
癌症致病基因，2的100次方种可能的基因图谱。
星系起源，2的350次方种可能的星云数据处理。
大脑运作机制，2的1000次可能的意识量子流。

面对这样数理级的运算，科学家别无选择，必须从可能的法则中选择一些可以信任的，并以此为基础建立理论模型。贝叶斯公式正好以严谨的数学形式帮他们实现了这一点。科学家把所有假设与已有知识、观测数据一起代入贝叶斯公式，就能得到明确的概率值。而要破译某种现象的成因网络，只需将公式本身也结成网络，即贝叶斯网络，接下来只需要向这个模型代入观测数据，通过网络节点间的贝叶斯公式重新计算出概率值。为每个新数据、每个连接重复这种计算，直到形成一个网络图，让任意两个原因之间的连接都得到精确的概率值为止。人类认知的缺陷越大，贝叶斯网络展示的力量越让人震撼。

但这还不是最可怕的，这里我们要引入“蜂群效应”，一只个体蜜蜂，基本上没有智力，但当它们组建成一个蜂群时，就会爆发出一种整体智力，拥有记忆能力，能制造出巧夺天工的蜂巢。贝叶斯网络的每一个节点就像一只蜜蜂，这种群体的连接不仅生动，而且非常严谨，一旦这个群体达到一定数量级别，有没有可能产生整体智慧？这不仅是哲学家需要思考的问题，生命学家需要讨论的问题，AI圈的科学家也应该直接去面对。

今天一场轰轰烈烈的“贝叶斯革命”正在AI界发生：贝叶斯公式已经渗入到工程师的骨子里，分类算法也成为主流算法。在很多人眼中，贝叶斯定理就是AI进化论的基石。