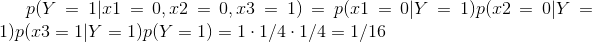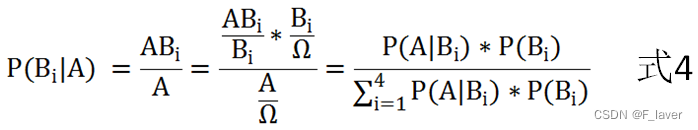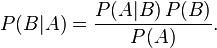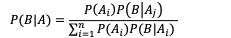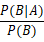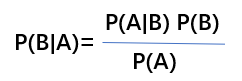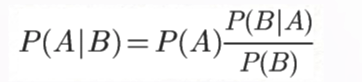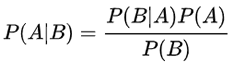引言
贝叶斯法则以托马斯.贝叶斯命名,他研究如何计算二项分布的概率参数的分布。贝叶斯法则被世界广泛认识,得益于Richard Price的推广和宣传。Price编辑了贝叶斯的主要著作《An Essay towards solving a Problem in the Doctrine of Chances》,在1763年贝叶斯去世2年后发表在Philosophical Transactions of the Royal Society of London。贝叶斯法则在概率论中的地位比肩勾股定理在几何学中的地位,现在成为统计推断中的重要方法,也是许多机器学习算法的核心。
推导
贝叶斯定理可以通过条件概率推导。图中A和B是两个事件,条件概率指某个事件发生后另外一个事件发生的概率。用数学符号表示,P(A|B)指事件B发生的条件下,事件A发生的概率。反之,P(B|A)指事件A发生的条件下,事件B发生的概率。下图黄色区域是A和B两个事件同时为真的概率,它既等于事件A发生的概率乘以事件A发生后事件B发生的条件概率,也等于它既等于事件B发生的概率乘以事件B发生后事件A发生的条件概率。
P(A)*P(B|A) = P(B)*P(A|B)
由上可以推导出:
P(A|B) = P(A)*P(B|A)/P(B)
这个计算事件B发生后事件A发生概率的公式就是大名鼎鼎的贝叶斯公式。

一个关于硬币的例子
概率论喜欢拿硬币来举例子,这里我们也举个硬币例子,主要是借用naturemethods上发表的一个直观的图示。我们有两个“公平”的硬币,掷硬币之后正面的概率都是50%,即P(H) = 50%。在这种情况下,选择特定硬币C和特定结果正面H的联合概率是它们各自概率的积,P(C,H) = P(C)*P(H)。倘若我们把其中一个硬币换成一个有偏向的硬币,这个硬币75%的抛掷结果是正面,这个时候硬币选择和正反面就不是独立事件。两个事件之间的关系可用上面提到的条件概率来表示,P(H|Cb) = 75%。

接下来,如果我们抛掷的结果是正面的,我们如何得知所选硬币是有偏向性的概率大小呢?用数学符号表示,我们想要知道P(Cb|H)的大小。根据贝叶斯公式:
P(Cb|H) = P(H|Cb)*P(Cb)/P(H)
P(Cb)是在抛掷硬币前我们对于硬币是有偏向的概率的“猜测”,即先验概率。而P(Cb|H)是硬币抛掷结果出来后,我们对于硬币是有偏向性的概率的重新“猜测”,即后验概率。P(H|Cb)等于0.75, P(Cb)等于0.5;而P(H)等于P(H|C)*P(C) + P(H|Cb)*P(Cb),等于0.625。根据贝叶斯公式,我们可知,P(Cb|H)等于0.6。由上,我们通过一次硬币抛掷结果,由先验概率获得后验概率。倘若硬币抛掷继续进行,我们有越来越多的“数据”,下一次抛掷结果还是正面(有人认定那个有偏向的硬币,出老千哦),我们可以用第一次获得的后验概率对原先假设的先验概率进行更新,然后从新利用贝叶斯公式计算新的后验概率。

一个关于疾病的例子
假设一种疾病有三种亚型,(X,Y,Z),它们的占比为0.6,0.3,0.1。X是最常见的,而Z是最罕见的。现在有一个诊断试剂盒,可以通过检测生物标记物A和B来进行疾病分型,在不同亚型中A和B能被检测到的概率已知。通过贝叶斯公式,P(X|A) = P(A|X)*P(X)/P(A),亚型X发生概率是已知的0.6,亚型X中标记物A阳性概率P(A|X)已知为0.2,这个时候只需要知道标记物A在这种疾病中被检测为阳性的概率,即各种亚型概率乘以各种亚型下标记物A为阳性的条件概率,最后求和。P(A) = 0.6 * 0.2 + 0.3 * 0.9 + 0.1 * 0.2 = 0.41。由贝叶斯公式计算得到,A标志物检测阳性亚型X概率为0.29,Y概率为0.66,Z概率为0.05。而B标志物检测阳性亚型X概率为0.44,Y概率为0.22,Z概率为0.33。尽管B标志物在亚型Z中检测到大概率达0.9,但由于亚型Z较为罕见,因而即便B标志物阳性了,这个时候概率最大的亚型还是亚型X。
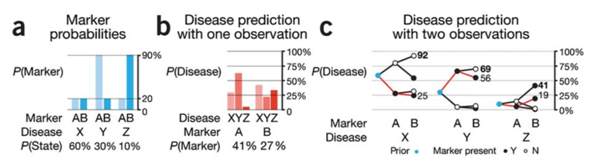
最后,上图c的展示很直观,我们对于特定亚型,一开始有一个先验的认识(蓝色点),随着我们收集越来越多的证据(标记物A,B表达),我们可以通过贝叶斯公式不断更新我们的认识(后验概率)。这个过程在一定程度上类似临床医生对于疾病的诊断与鉴别诊断,通过病人的主诉已经临床表现,医生对于病人所患疾病有一个初步判断,随着越来越多检查结果出来,医生也在不断更新自己最初的判断。只不过医生借助的是人脑,不是电脑。
突变检测
基因组数据分析的一个重要方面是发现样本中的突变,在生信分析中,这个任务叫“mutationcall”。在实现上面,贝叶斯法则提供了非常好的解决方案。在这个任务中,我们拥有的“数据”是测序得到的序列,我们想要推断的是各个位点的基因型。常用分析工具GATK流程通过贝叶斯公式计算各种可能基因型的似然性,确定该位点最可能的基因型。
P(G|D)=P(G)P(D|G)/∑iP(Gi)P(D|Gi)
P(G|D)是在观测数据下特定基因型出现的条件概率,而分母是通过全概率公式计算出来的P(D),对于所有的基因型都一样。不同基因型的区别主要在分子,P(G)是不同基因型的先验概率,而P(D|G)是特定基因型下得到观测序列(数据)的条件概率。
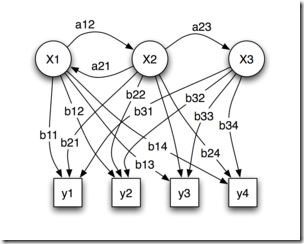
细胞网络搭建
现在单细胞技术非常流行,研究人员可以收集到单细胞水平的基因组、转录组、表观组和蛋白组数据。而早在十几年前,当主流的单细胞技术还是流式细胞术,多参数流式检测极限也就十来个靶点的时候,计算生物学家们就在尝试利用贝叶斯推断来构建细胞网络。如果能够将这种研究思路拓展到不同的细胞亚群、组织、器官甚至模式生物整体,贝叶斯推断在多层次建模中必然大有可为。

小结
法兰西学院实验心理学教授Stanislas Dehaene时常挂在嘴边的一句话是,“我们每个人大脑里都有一个小Thomas Bayes”。Dehaene经常告诉学生们,“贝叶斯公式虽然是数学,但它是关于思考的数学。”。贝叶斯公式的神奇之处在于它似乎无所不能,在癌症研究中基于贝叶斯法则的算法被用于单细胞转录组差异表达基因分析、细胞聚类、药物敏感性预测和癌症驱动基因的判定。而在癌症研究之外,贝叶斯的幽灵几乎无处不在。
一个小测试
如果你看到这里,而且你刚好还有点时间,可以试着用贝叶斯公式解一下这个问题:
有个疾病发病率为1%,某个诊断测试号称准确率达到99%可以诊断这个疾病:患者有99%的机会被这个诊断测试发现;正常人还是存在1%的阳性率(假阳性率)。问题来了,如果小明测试阳性,那么小明真正有病的概率是多大?
参考文献
1. Bayes, T., Price, R. An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, A.M.F.R.S. Philosophical Transactions of the Royal Society of London, 1963. 53(0):370-418.
2. Jansen, R., et al. A Bayesian networks approach for predicting protein-protein interactions from genomic data. Science, 2003. 302(5644):449-453.
3. Akavia, U.D., et al. An integrated approach to uncover drivers of cancer. Cell, 2010. 143(6):1005-1017.
4. Li, H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics, 2011. 27(21):2987-2993.
5. Costello, J.C., et al. A community effort to assess and improve drug sensitivity prediction algorithms. Nat Biotechnol, 2014. 32(12):1202-1212.
6. Kharchenko, P.V., Silberstein, L., Scadden, D.T. Bayesian approach to single-cell differential expression analysis. Nat Methods, 2014. 11(7):740-742.
7. Roth, A., et al. PyClone: statistical inference of clonal population structure in cancer. Nat Methods, 2014. 11(4):396-398.
8. Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature, 2015. 521(7553):452-459.
9. Puga, J.L., Krzywinski, M., Altman, N. Bayes’ theorem. Nature Methods, 2015. 12(4):277-278.
10. Puga, J.L., Krzywinski, M., Altman, N. Points of Significance. Bayesian networks. Nat Methods, 2015. 12(9):799-800.
11. Azizi, E., et al. Single-Cell Map of Diverse Immune Phenotypes in the Breast Tumor Microenvironment. Cell, 2018. 174(5):1293-1308 e1236.
12. Eling, N., et al. Correcting the Mean-Variance Dependency for Differential Variability Testing Using Single-Cell RNA Sequencing Data. Cell Syst, 2018. 7(3):284-294 e212.