逻辑回归模型及应用

本次实验对于使用机器学习完成分类与预测任务的基本流程。
数据集导入->训练集和测试集的划分->数据标准化->模型导入与训练->测试集结果预测->分类情况可视化->混淆矩阵以及多指标精度评价。
以及使用sklearn库中的逻辑模型，数据预处理，数据集进行具体操作。
最后使用seaborn进行散点图的绘制。使用基础的精度评估指标评价模型。
sklearn库中的preprocessing.StandardScaler()函数做了一个减均值除方差的过程。

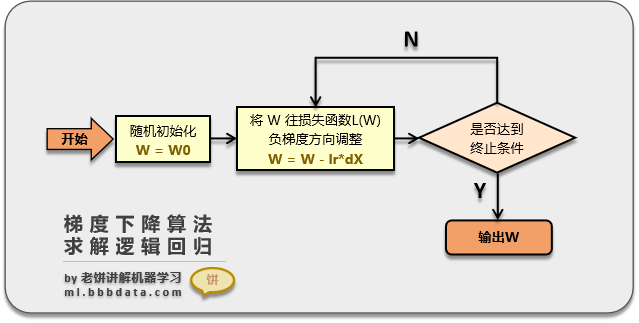
线性函数为表达式为：Y=KX+B;
其中K为1*n维向量，对应X的“权重占比”。加上一个偏置B进行计算
逻辑函数为sigmoid函数：非线性转化二分类处理

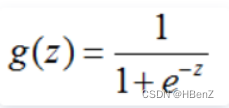
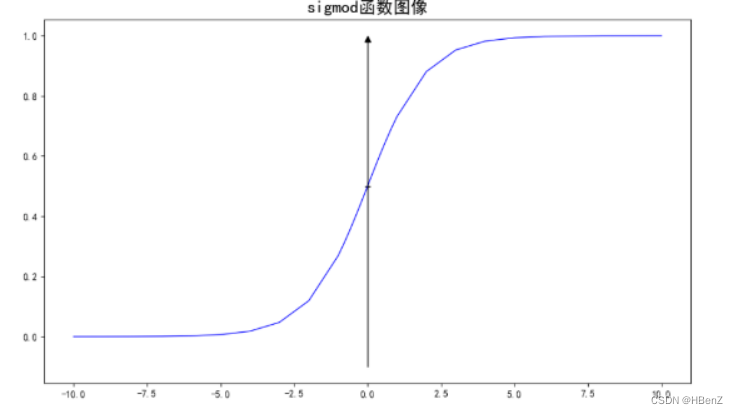
将两者结合构成逻辑回归函数：

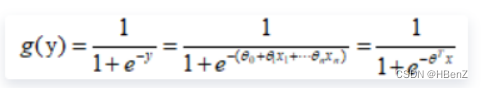
用与进行二分类。
处理多分类任务时，sklearn中的logistic函数会使用多个逻辑回归函数进行比较分类，以达到分类效果。
内容一：对sklearn库中的鸢尾花数据集进行提取分析。抽取部分数据：花瓣长度、花瓣宽度和两个类别：0，1类，利用逻辑回归模型进行二分类。熟悉使用流程
(1)数据集导入
(2)训练集和测试集的划分
(3)数据标准化
(4)模型导入与训练
(5)测试集结果预测
(6)分类情况可视化
(7)混淆矩阵以及多指标精度评价

#数据以及库的导入
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets  # 导入数据库
from sklearn import model_selection
from sklearn import preprocessing
from sklearn import linear_modeliris = datasets.load_iris()  # 导入鸢尾花数据
print(iris.data.shape,iris.target.shape)  #数据大小
print(iris.feature_names)  # 相关特征名称
#创建dataframe数据结构
iris_feature=pd.DataFrame(iris.data,columns=iris.feature_names)
iris_target=pd.DataFrame(iris.target,columns=['species'])
#按列进行dataframe的数据连接
irisData=pd.concat([iris_feature,iris_target],axis=1)

#定义函数用于绘制热力图
def Hotimg(conm):plt.imshow(conm,cmap=plt.cm.Blues)plt.xticks(range(len(conm)),iris.target_names)plt.yticks(range(len(conm)),iris.target_names)plt.colorbar()plt.xlabel("Labels")plt.ylabel("Predicted labels")plt.title("confusion of Log")#显示数值for i in range(len(conm)):for j in range(len(conm)):plt.text(i,j,conm[j][i])plt.show()

#筛选用于二分类的数据，类别为0，1的
irisData=irisData[irisData['species']<2]
#数据集的划分model_selection中train_test_split(Data,size):待划分数据，测试集占比 
train_set,test_set=model_selection.train_test_split(irisData,test_size=0.2)
#输出用于观察
print(train_set.shape)
print(test_set.shape)
train_set

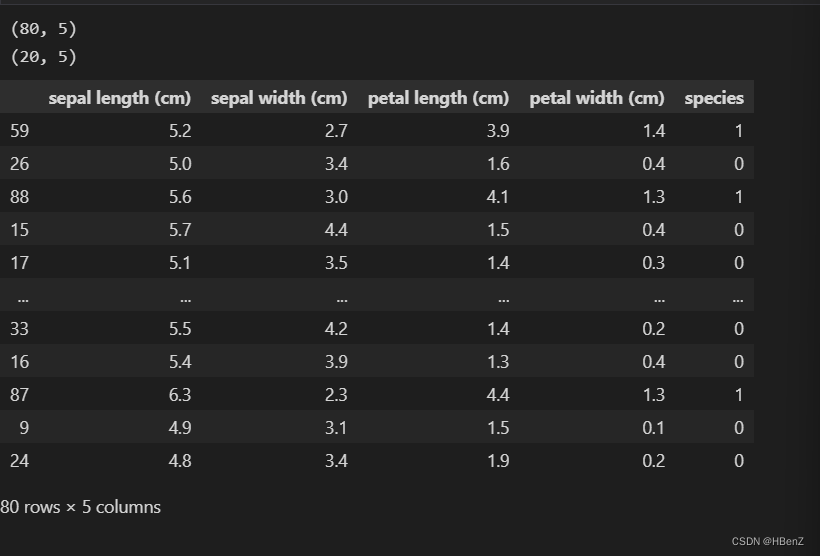
#数据预处理
transform= preprocessing.StandardScaler()
#对测试集和验证机分别进行标准化预处理
X_train=transform.fit_transform(train_set[['petal length (cm)','petal width (cm)']])
X_test=transform.fit_transform(test_set[['petal length (cm)','petal width (cm)']])
#标准分类
Y_train=train_set['species']
Y_test=test_set['species']

#模型导入
#从线性模型中选择逻辑回归模型
lgr=linear_model.LogisticRegression()
#使用训练集数据训练模型
lgr.fit(X_train,Y_train)
#获得模型参数进行数据类型转化
#参数：coef*X+intercept=Y
coef,intercept=np.array(lgr.coef_),np.array(lgr.intercept_)
#对测试集进行预测
y_pred=lgr.predict(X_test)
y_pred

#分界情况可视化
#制作x横坐标范围为训练数据中极小值到极大值，间隔为0.1
x1=np.arange(X_train[:,0].min(),X_train[:,0].max(),step=0.1)
#y=k0*x0+k1*k1+b && y=0时为分界点 => x1=-(x1*k1+b)/k0
x2=pd.DataFrame(0-(x1*coef[0][0]+intercept)/coef[0][1],columns=["petal width"])
#转为dataframe数据结构
x1=pd.DataFrame(x1,columns=["petal length"])
#按列拼接合成dataframe
x=pd.concat([x1,x2],axis=1)
#添加分界线，设置x,y轴标签，数据内容,颜色
sns.relplot(x='petal length',y='petal width',data=x,color='r')
#添加训练集中的散点，以训练集中不同标签作为类别划分
sns.scatterplot(x=X_train[:,0],y=X_train[:,1],hue=Y_train)

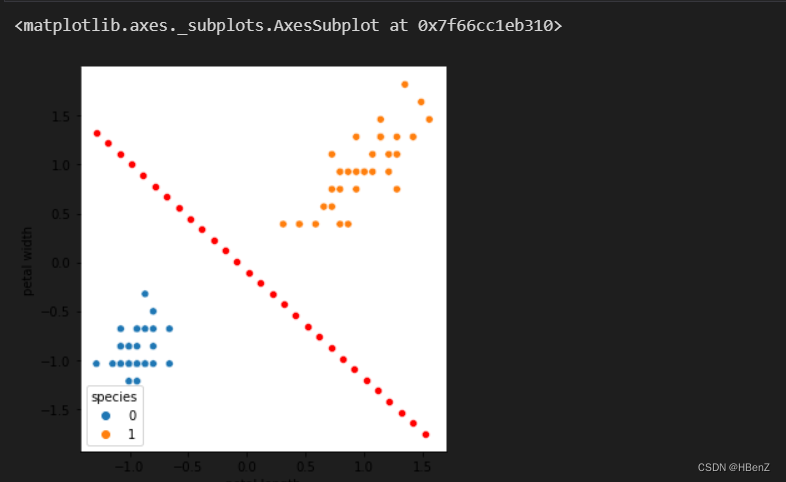
#使用sklearn中的confusion_matrix计算混淆矩阵
from sklearn import metrics
conm=metrics.confusion_matrix(y_pred,Y_test)
Hotimg(conm)
#识别准确度
accuracy=np.sum(conm,axis=0)[0]/sum(sum(conm))
print("Accuracy:{0}".format(accuracy))
#识别精度
precision=conm[0,0]/np.sum(conm,axis=0)[0]
print("Precision:{0}".format(precision))
#反馈率
recall=conm[0,0]/(conm[0,0]+conm[1,1])
print("Recall:{0}".format(recall))

内容二：使用全部属性，用逻辑回归分类所有类型的鸢尾花。详细步骤以及精度评价
(1)数据集导入
(2)训练集和测试集的划分
(3)数据标准化
(4)模型导入与训练
(5)测试集结果预测
(6)分类情况可视化
(7)混淆矩阵以及多指标精度评价

#数据以及库的导入
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets  # 导入数据库
from sklearn import model_selection
from sklearn import preprocessing
from sklearn import linear_modeliris = datasets.load_iris()  # 导入鸢尾花数据
print(iris.data.shape,iris.target.shape)  #数据大小
print(iris.feature_names)  # 相关特征名称
#创建dataframe数据结构
iris_feature=pd.DataFrame(iris.data,columns=iris.feature_names)
iris_target=pd.DataFrame(iris.target,columns=['species'])
#按列进行dataframe的数据连接
irisData=pd.concat([iris_feature,iris_target],axis=1)

#数据集和测试集的划分
#设置训练集：测试集比例为8:2
train_set,test_set=model_selection.train_test_split(irisData,test_size=0.2)
print(train_set.shape)
print(test_set.shape)

#数据标准化
transform=preprocessing.StandardScaler()
#分别对训练集和验证机进行标准化
x_train=transform.fit_transform(train_set[["sepal length (cm)","sepal width (cm)","petal length (cm)","petal width (cm)"]])
x_test=transform.fit_transform(test_set[["sepal length (cm)","sepal width (cm)","petal length (cm)","petal width (cm)"]])
#标签分类
y_train=train_set['species']
y_test=test_set['species']

#模型导入与训练
lgr=linear_model.LogisticRegression()
#训练
lgr.fit(x_train,y_train)
#获得模型参数
coef,intercept=np.array(lgr.coef_),np.array(lgr.intercept_)
#预测
y_pred=lgr.predict(x_test)
y_pred

#绘制图片，由于四维或者三维图不好画，所以以sepal length (cm)	sepal width (cm)为轴绘图
x_train=irisData[["petal length (cm)","petal width (cm)"]]
#制作x横坐标范围为训练数据中极小值到极大值，间隔为0.1
x1=np.arange(x_train['petal length (cm)'].min(),x_train['petal width (cm)'].max(),step=0.1)
#转为dataframe数据结构
x1=pd.DataFrame(x1,columns=["petal length"])
#添加训练集中的散点，以训练集中不同标签作为类别划分
sns.scatterplot(x=x_train['petal length (cm)'],y=x_train['petal width (cm)'],hue=irisData['species'])#打印输出逻辑回归函数中用于二分类的三条线性函数
print("y1={:.3}*sepal length+{:.3}*sepal width+{:.3}*petal length+{:.3}*peetal width+{:.3}".format(coef[0][0],coef[0][1],coef[0][2],coef[0][3],intercept[0]))
print('y2={:.3}*sepal length+{:.3}*sepal width+{:.3}*petal length+{:.3}*peetal width+{:.3}'.format(coef[1][0],coef[1][1],coef[1][2],coef[1][3],intercept[1]))
print('y3={:.3}*sepal length+{:.3}*sepal width+{:.3}*petal length+{:.3}*peetal width+{:.3}'.format(coef[2][0],coef[2][1],coef[2][2],coef[2][3],intercept[2]))

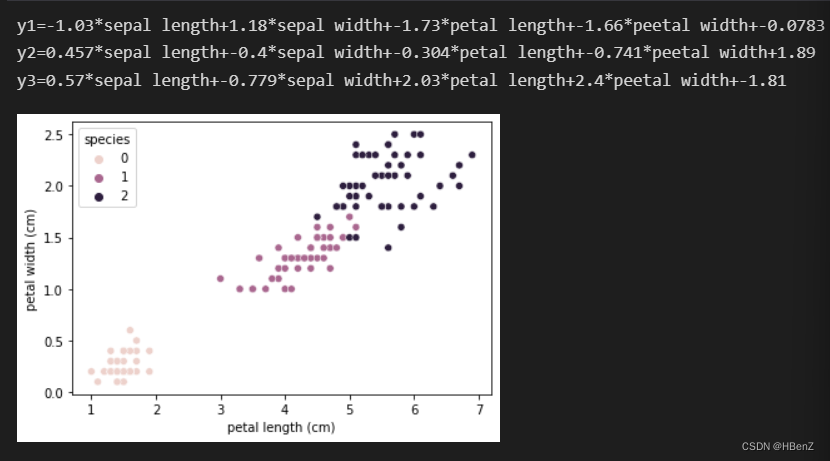
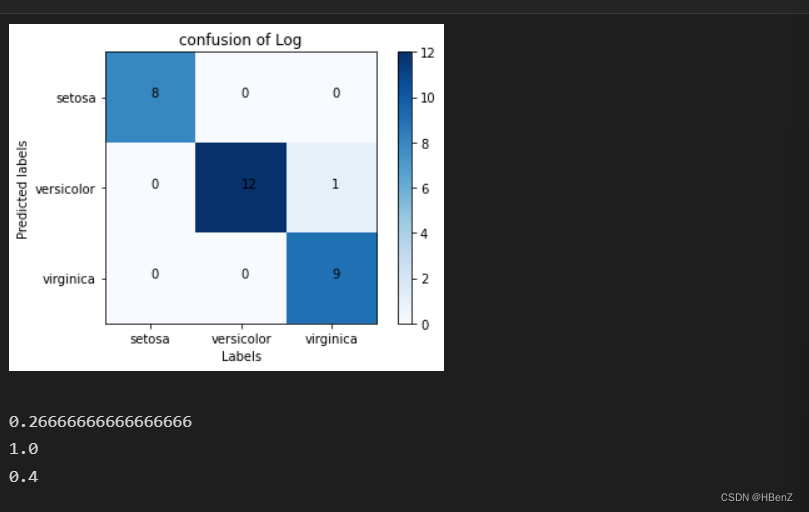
#混淆矩阵
from sklearn import metrics
conm=metrics.confusion_matrix(y_pred,y_test)
Hotimg(conm)
#精确率计算
accuracy=np.sum(conm,axis=0)[0]/sum(sum(conm))
print(accuracy)
#识别精度
precision=conm[0,0]/np.sum(conm,axis=0)[0]
print(precision)
#召回率
recall=conm[0,0]/(conm[0,0]+conm[1,1])
print(recall)