一、引言
线性回归的因变量是连续变量,而逻辑回归解决的是因变量是分类变量的问题。当然,自变量既可以是连续的也可以是分类的,但是分类变量做自变量前需要做哑变量处理。
逻辑回归将分类因变量的0、1等 值转换为取其值的概率,将二分类模型转换为线性函数模型,转换后模型课表示为
l n p ( y = 1 ) 1 − p ( y = 1 ) = β 0 + β 1 x 1 + . . . + β p x p + ε ln\frac{p(y=1)}{1-p(y=1)}=\beta_{0}+\beta_{1}x_{1}+...+\beta_{p}x_{p}+\varepsilon ln1−p(y=1)p(y=1)=β0+β1x1+...+βpxp+ε
即 l n E ( y ) 1 − E ( y ) ln\frac{E(y)}{1-E(y)} ln1−E(y)E(y)是 x 1 , x 2 , . . . , x p x_{1},x_{2},...,x_{p} x1,x2,...,xp的线性函数, l o g i t [ p ( y = 1 ) ] = l n [ p ( y = 1 ) 1 − p ( y = 1 ) ] logit[p(y=1)]=ln[\frac{p(y=1)}{1-p(y=1)}] logit[p(y=1)]=ln[1−p(y=1)p(y=1)]就是Logit转换。也可以转换为
p ( y = 1 ) = e x p ( β 0 + β 1 x 1 + . . . + β p x p ) 1 + e x p ( β 0 + β 1 x 1 + . . . + β p x p ) p(y=1)= \frac{exp(\beta_{0}+\beta_{1}x_{1}+...+\beta_{p}x_{p})}{1+exp(\beta_{0}+\beta_{1}x_{1}+...+\beta_{p}x_{p})} p(y=1)=1+exp(β0+β1x1+...+βpxp)exp(β0+β1x1+...+βpxp)
二、回归模型估算方法
Logistic回归模型有两种估算方法,一种是加权最小二乘法估计,用于分组数据的Logistic回归模型;另一种是最大似然估计,用于未分组数据的Logistic回归模型。
2.1 分组数据的Logistic回归模型
分组数据的Logistic回归模型也可以称为分层逻辑回归,分类因变量的每一个可能取值 都能得到一个属于此取值的样本,且样本由此取值对应的原始数据统计得到,然后得到回归模型。这种方式的回归样本数 等于 分类因变量可能取值的个数。
下表9-5为例,分类因变量一共有9个可能取值,即 i = 1 , 2 , . . . , 9 i=1,2,...,9 i=1,2,...,9。用家庭收入 x x x作为自变量(由每一类可能取值对应的原始数据的平均值得到),回归模型为 p i ′ = β 0 + β 1 x , p i ′ = l n p i 1 − p i {p_{i}}'=\beta_{0}+\beta_{1}x,{p_{i}}'=ln\frac{p_{i}}{1-p_{i}} pi′=β0+β1x,pi′=ln1−pipi,回归样本数为9。

对于每一个因变量的取值(对于每一个样本 i = 1 , 2 , . . . , 9 i=1,2,...,9 i=1,2,...,9):
p i = e x p ( β 0 + β 1 x i 1 + . . . + β p x i p ) 1 + e x p ( β 0 + β 1 x i 1 + . . . + β p x i p ) , i = 1 , 2 , . . . , 9 p_{i}= \frac{exp(\beta_{0}+\beta_{1}x_{i1}+...+\beta_{p}x_{ip})}{1+exp(\beta_{0}+\beta_{1}x_{i1}+...+\beta_{p}x_{ip})}, i=1,2,...,9 pi=1+exp(β0+β1xi1+...+βpxip)exp(β0+β1xi1+...+βpxip),i=1,2,...,9
即
l n p i 1 − p i = β 0 + β 1 x i 1 + . . . + β p x i p , i = 1 , 2 , . . . , n ln\frac{p_{i}}{1-p_{i}}=\beta_{0}+\beta_{1}x_{i1}+...+\beta_{p}x_{ip}, i=1,2,...,n ln1−pipi=β0+β1xi1+...+βpxip,i=1,2,...,n
用9个样本回归后,得到
p ^ = e x p ( β 0 ^ + β 1 ^ x 1 + . . . + β p ^ x p ) 1 + e x p ( β 0 ^ + β 1 ^ x 1 + . . . + β p ^ x p \widehat{p}= \frac{exp(\widehat{\beta_{0}}+\widehat{\beta_{1}}x_{1}+...+\widehat{\beta_{p}}x_{p})}{1+exp(\widehat{\beta_{0}}+\widehat{\beta_{1}}x_{1}+...+\widehat{\beta_{p}}x_{p}} p =1+exp(β0 +β1 x1+...+βp xpexp(β0 +β1 x1+...+βp xp)
为了避免异方差,采用加权最小二程的方式获得回归参数的估计值 β 0 ^ , β 1 ^ , . . . , β p ^ \widehat{\beta_{0}},\widehat{\beta_{1}},...,\widehat{\beta_{p}} β0 ,β1 ,...,βp ,加权权重的计算方式为
w i = n i p i ( 1 − p i ) w_{i}=n_{i}p_{i}(1-p_{i}) wi=nipi(1−pi)
注:分组数据的Logistic回归只适用于大样本的分组数据,对小样本的未分组数据不适用,并且组数即为回归拟合的样本数,容易造成拟合精度不够。一般情况下,多采用极大似然估计直接拟合未分组数据的Logistic回归模型。
2.2 未分组数据的Logistic回归模型
假设 n n n组样本 ( x i 1 , x i 2 , . . . , x i p ; y i ) , i = 1 , 2 , . . . , n (x_{i1},x_{i2},...,x_{ip};y_{i}),i=1,2,...,n (xi1,xi2,...,xip;yi),i=1,2,...,n,其中 y 1 , y 2 , . . . , y n y_{1},y_{2},...,y_{n} y1,y2,...,yn是取值为0或1的随机变量, x 1 , x 2 , . . . , x p x_{1},x_{2},...,x_{p} x1,x2,...,xp是与 y y y 相关的确定性变量。对于每一个样本有
p i = e x p ( β 0 + β 1 x i 1 + . . . + β p x i p ) 1 + e x p ( β 0 + β 1 x i 1 + . . . + β p x i p ) , i = 1 , 2 , . . . , n p_{i}= \frac{exp(\beta_{0}+\beta_{1}x_{i1}+...+\beta_{p}x_{ip})}{1+exp(\beta_{0}+\beta_{1}x_{i1}+...+\beta_{p}x_{ip})}, i=1,2,...,n pi=1+exp(β0+β1xi1+...+βpxip)exp(β0+β1xi1+...+βpxip),i=1,2,...,n
即
l n p i 1 − p i = β 0 + β 1 x i 1 + . . . + β p x i p , i = 1 , 2 , . . . , n ln\frac{p_{i}}{1-p_{i}}=\beta_{0}+\beta_{1}x_{i1}+...+\beta_{p}x_{ip}, i=1,2,...,n ln1−pipi=β0+β1xi1+...+βpxip,i=1,2,...,n
用 n n n个样本回归后,得到
p ^ = e x p ( β 0 ^ + β 1 ^ x 1 + . . . + β p ^ x p ) 1 + e x p ( β 0 ^ + β 1 ^ x 1 + . . . + β p ^ x p \widehat{p}= \frac{exp(\widehat{\beta_{0}}+\widehat{\beta_{1}}x_{1}+...+\widehat{\beta_{p}}x_{p})}{1+exp(\widehat{\beta_{0}}+\widehat{\beta_{1}}x_{1}+...+\widehat{\beta_{p}}x_{p}} p =1+exp(β0 +β1 x1+...+βp xpexp(β0 +β1 x1+...+βp xp)
与分组数据回归不同的是,样本存在相同的 y y y值, y y y值相同的样本 p i p_{i} pi 值和 l n p i 1 − p i ln\frac{p_{i}}{1-p_{i}} ln1−pipi 值相等。
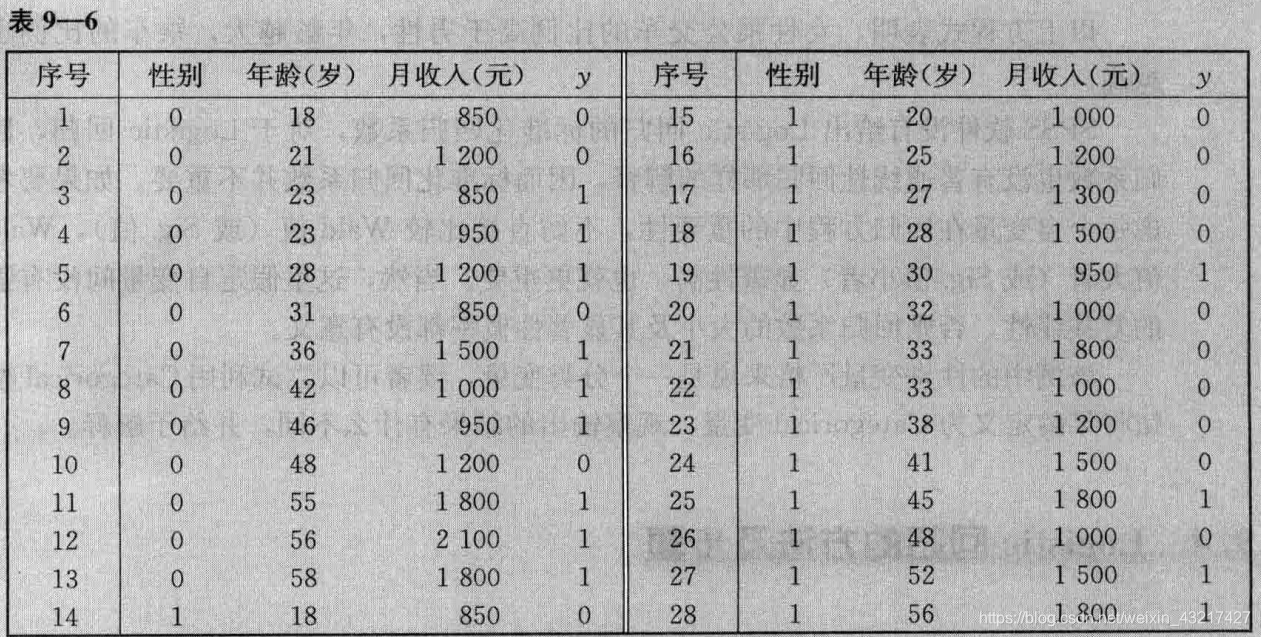
利用 n n n组样本回归得到Logistic回归模型,样本以表9-6为例 n = 28 n=28 n=28
这种模型采用最大似然估计获得回归参数,假设为二分类逻辑回归模型,其思路定义因变量 y y y的联合概率密度为
P ( y i ) = π i y i ( i − π i ) 1 − y i , y i = 0 , 1 ; i = 1 , 2 , . . . , n P(y_{i})=\pi_{i}^{y_{i}}(i-\pi_{i})^{1-y_{i}},y_{i}=0,1;i=1,2,...,n P(yi)=πiyi(i−πi)1−yi,yi=0,1;i=1,2,...,n
其中 π i = e x p ( β 0 + β 1 x 1 + . . . + β p x p ) 1 + e x p ( β 0 + β 1 x 1 + . . . + β p x p ) \pi_{i}= \frac{exp(\beta_{0}+\beta_{1}x_{1}+...+\beta_{p}x_{p})}{1+exp(\beta_{0}+\beta_{1}x_{1}+...+\beta_{p}x_{p})} πi=1+exp(β0+β1x1+...+βpxp)exp(β0+β1x1+...+βpxp),于是 y 1 , y 2 , . . . , y n y_{1},y_{2},...,y_{n} y1,y2,...,yn的似然函数为:
L = ∏ i = 1 n P ( y i ) = ∏ i = 1 n π i y i ( i − π i ) 1 − y i L=\prod _{i=1}^nP(y_{i})=\prod _{i=1}^n\pi_{i}^{y_{i}}(i-\pi_{i})^{1-y_{i}} L=i=1∏nP(yi)=i=1∏nπiyi(i−πi)1−yi
取对数后
l n L = ∑ i = 1 n y i ( β 0 + β 1 x i 1 + . . . + β p x i p ) − ∑ i = 1 n l n [ 1 + e x p ( β 0 + β 1 x i 1 + . . . + β p x i p ) ] lnL=\sum_{i=1}^ny_{i}(\beta_{0}+\beta_{1}x_{i1}+...+\beta_{p}x_{ip})-\sum_{i=1}^nln[1+exp(\beta_{0}+\beta_{1}x_{i1}+...+\beta_{p}x_{ip})] lnL=i=1∑nyi(β0+β1xi1+...+βpxip)−i=1∑nln[1+exp(β0+β1xi1+...+βpxip)]
用数值计算得到参数估计值 β 0 ^ , β 1 ^ , . . . , β p ^ \widehat{\beta_{0}},\widehat{\beta_{1}},...,\widehat{\beta_{p}} β0 ,β1 ,...,βp 。
参考书:《多元统计分析》何晓群