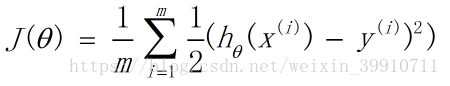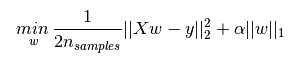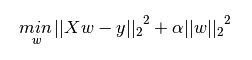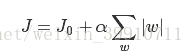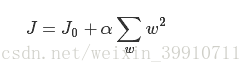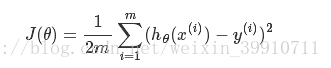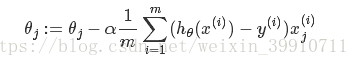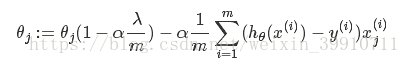目录
1 LR
1.1 直观表述
1.2 决策边界(Decision Boundary)
2. 权值求解
2.1 代价函数(似然函数)
2.1.1 为什么损失函数不用最小二乘?即逻辑斯蒂回归损失函数为什么使用交叉熵而不是MSE?
2.1.2 代价函数
2.2 似然函数的求解-梯度下降
3 加入正则项
3.1 正则解释
3.2 L1和L2正则化的直观理解
3.2.1 L1正则化和特征选择
3.2.2 L2正则化和过拟合
4 如何用逻辑回归处理多标签问题
4.1 One vs One
4.2 One vs All
4.3 从sigmoid函数到softmax函数的推导
5 为什么逻辑斯蒂回归的输出值可以作为概率
6 逻辑斯蒂回归是否可以使用其他的函数替代 sigmoid 函数
线性分类器:模型是参数的线性函数,分类平面是(超)平面;
非线性分类器:模型分界面可以是曲面或者超平面的组合。
典型的线性分类器有感知机,LDA,逻辑斯特回归,SVM(线性核);
典型的非线性分类器有朴素贝叶斯(有文章说这个本质是线性的,http://dataunion.org/12344.html),kNN,决策树,SVM(非线性核)
逻辑回归模型(Logistic Regression, LR)基础 - 文墨 - 博客园
细品 - 逻辑回归(LR)* - ML小菜鸟 - 博客园
当你的目标变量是分类变量时,才会考虑逻辑回归,并且主要用于两分类问题。
1 LR
LR模型可以被认为就是一个被Sigmoid函数(logistic方程)所归一化后的线性回归模型!
逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,使得逻辑回归模型成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。
1.1 直观表述
首先来解释一下的表示的是啥?它表示的就是将因变量预测成1(阳性)的概率,具体来说它所要表达的是在给定x条件下事件y发生的条件概率,而
是该条件概率的参数。将它分解一下:
(1)式就是我们介绍的线性回归的假设函数,那(2)式就是我们的Sigmoid函数啦。
由于线性回归在整个实数域内敏感度一致,而分类范围,需要在[0,1]。逻辑回归就是一种减小预测范围,将预测值限定为[0,1]间的一种回归模型,其回归方程与回归曲线如下图所示。逻辑曲线在z=0时,十分敏感,在z>>0或z<<0处,都不敏感,将预测值限定为(0,1)。为什么会用Sigmoid函数?因为它引入了非线性映射,将线性回归值域映射到0-1之间,有助于直观的做出预测类型的判断:大于等于0.5表示阳性,小于0.5表示阴性。
其实,从本质来说:在分类情况下,经过学习后的LR分类器其实就是一组权值,当有测试样本输入时,这组权值与测试数据按照加权得到
这里的就是每个测试样本的n个特征值。之后在按照Sigmoid函数的形式求出
,从而去判断每个测试样本所属的类别。
由此看见,LR模型学习最关键的问题就是研究如何求解这组权值!
1.2 决策边界(Decision Boundary)
在LR模型中我们知道:当假设函数,即
,此时我们预测成正类;反之预测为负类。由图来看,我们可以得到更加清晰的认识。下图为Sigmoid函数,也是LR的外层函数。我们看到当
时,此时
(即内层函数
),然而此时也正是将y预测为1的时候;同理,我们可以得出内层函数
时,我们将其预测成0(即负类)。
逻辑回归的假设函数可以表示为
,
(和1.1节中的h不一样)
于是我们得到了这样的关系式:
下面再举一个例子,假设我们有许多样本,并在图中表示出来了,并且假设我们已经通过某种方法求出了LR模型的参数(如下图)。
根据上面得到的关系式,我们可以得到:
而我们再图像上画出得到:
这时,直线上方所有样本都是正样本y=1,直线下方所有样本都是负样本y=0。因此我们可以把这条直线成为决策边界。
同理,对于非线性可分的情况,我们只需要引入多项式特征就可以很好的去做分类预测,如下图:
值得注意的一点,决策边界并不是训练集的属性,而是假设本身和参数的属性。因为训练集不可以定义决策边界,它只负责拟合参数;而只有参数确定了,决策边界才得以确定。
2. 权值求解
2.1 代价函数(似然函数)
2.1.1 为什么损失函数不用最小二乘?即逻辑斯蒂回归损失函数为什么使用交叉熵而不是MSE?
面试题解答6:逻辑斯蒂回归为什么使用交叉熵而不是MSE - 知乎
- 从逻辑的角度出发,我们知道逻辑斯蒂回归的预测值是一个概率,而交叉熵又表示真实概率分布与预测概率分布的相似程度,因此选择使用交叉熵。
- 从MSE的角度来说,预测的概率与欧氏距离没有任何关系,并且在分类问题中,样本的值不存在大小关系,与欧氏距离更无关系,因此不适用MSE。
(1)原因一:损失函数的凸性(使用MSE可能会陷入局部最优)
前面我们介绍线性回归模型时,给出了线性回归的代价函数的形式(误差平方和函数),具体形式如下:
这里我们想到逻辑回归也可以视为一个广义的线性模型,那么线性模型中应用最广泛的代价函数-误差平方和函数,可不可以应用到逻辑回归呢?首先告诉你答案:是不可以的! 那么为什么呢? 这是因为LR的假设函数的外层函数是Sigmoid函数,Sigmoid函数是一个复杂的非线性函数,这就使得我们将逻辑回归的假设函数带入上式时,我们得到的
是一个非凸函数,如下图:
这样的函数拥有多个局部极小值,这就会使得我们在使用梯度下降法求解函数最小值时,所得到的结果并非总是全局最小,而有更大的可能得到的是局部最小值。这样解释应该理解了吧。
以 MSE 为损失函数的逻辑斯蒂回归就是一个非凸函数,如何证明这一点呢,要证明一个函数的凸性,只要证明其二阶导恒大于等于0即可,如果不是恒大于等于0,则为非凸函数。
让我们对上文中求得的 MSE 一阶导数继续求二阶导:

我们知道真实 label yi 只能取1和0,当yi=1时,上式取值范围为(-4,3),当yi=0时,上式取值范围为(-3,2),因此二阶导不恒大于等于0,因此MSE损失函数为非凸函数。
(2)原因二:MSE 的损失小于交叉熵的损失,导致对分类错误的点的惩罚不够
平方损失在训练的时候会出现一定的问题。当预测值与真实值之间的差距过大时,这时候参数的调整就需要变大,但是如果使用平方损失,训练的时候可能看到的情况是预测值和真实值之间的差距越大,参数调整的越小,训练的越慢。
如果使用平方损失作为损失函数,损失函数如下

其中 ![]() 表示真实值,
表示真实值,![]() 表示预测值。
表示预测值。
对参数求梯度
由此可以看出,参数![]() 除了跟真实值与预测值之间的差距有关外,还和激活函数的该点的导数有关,跟激活函数的梯度成正比,常见的激活函数是
除了跟真实值与预测值之间的差距有关外,还和激活函数的该点的导数有关,跟激活函数的梯度成正比,常见的激活函数是![]() 函数,当这个点越靠近上边或者下边的时候梯度会变得非常小,这样会导致当真实值与预测值差距很大时,参数变化的非常缓慢,与我们的期望不符合。
函数,当这个点越靠近上边或者下边的时候梯度会变得非常小,这样会导致当真实值与预测值差距很大时,参数变化的非常缓慢,与我们的期望不符合。
而使用交叉熵损失在更新参数的时候,当误差越大时,梯度也就越大,参数调整也能更大更快。
2.1.2 代价函数
虽然前面的解释否定了我们猜想,但是也给我们指明了思路,那就是我们现在要做的就是为LR找到一个凸的代价函数! 在逻辑回归中,我们最常用的损失函数为对数损失函数,对数损失函数可以为LR提供一个凸的代价函数,有利于使用梯度下降对参数求解。为什么对数函数可以做到这点呢? 我们先看一下对数函数的图像:
蓝色的曲线表示的是对数函数的图像,红色的曲线表示的是负对数的图像,该图像在0-1区间上有一个很好的性质,如图粉红色曲线部分。在0-1区间上当z=1时,函数值为0,而z=0时,函数值为无穷大。这就可以和代价函数联系起来,在预测分类中当算法预测正确其代价函数应该为0;当预测错误,我们就应该用一个很大代价(无穷大)来惩罚我们的学习算法,使其不要轻易预测错误。这个函数很符合我们选择代价函数的要求,因此可以试着将其应用于LR中。对数损失在LR中表现形式如下:
对于惩罚函数Cost的这两种情况:
给我们的直观感受就是:当实际标签和预测结果相同时,即y和同时为1或0,此时代价最小为0; 当实际标签和预测标签恰好相反时,也就是恰好给出了错误的答案,此时惩罚最大为正无穷。现在应该可以感受到对数损失之于LR的好了。
为了可以更加方便的进行后面的参数估计求解,我们可以把Cost表示在一行:
这与我们之前给出的两行表示的形式是等价的。因此,我们的代价函数最终形式为:
该函数是一个凸函数,这也达到了我们的要求。这也是LR代价函数最终形式。
2.2 似然函数的求解-梯度下降
代价函数的求导过程
Sigmoid函数的求导过程:
故,sigmoid函数的导数
损失函数梯度求解过程:
故,参数更新公式为:
3 加入正则项
3.1 正则解释
正则:机器学习中正则化项L1和L2的直观理解_阿拉丁吃米粉的博客-CSDN博客_l1 l2正则化
此时的w为。
对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
此时加入的正则化项,是解决过拟合问题。
下图是Python中Lasso回归的损失函数,式中加号后面一项![]() 即为L1正则化项。
即为L1正则化项。
下图是Python中Ridge回归的损失函数,式中加号后面一项![]() 即为L2正则化项。
即为L2正则化项。
一般回归分析中回归w表示特征的系数,从上式可以看到正则化项是对系数做了处理(限制)。L1正则化和L2正则化的说明如下:
- L1正则化是指权值向量w中各个元素的绝对值之和,通常表示为
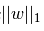
- L2正则化是指权值向量w中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号),通常表示为
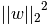
一般都会在正则化项之前添加一个系数,Python中用α表示,一些文章也用λ表示。这个系数需要用户指定。
那添加L1和L2正则化有什么用?下面是L1正则化和L2正则化的作用,这些表述可以在很多文章中找到。
- L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
- L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
3.2 L1和L2正则化的直观理解
这部分内容将解释为什么L1正则化可以产生稀疏模型(L1是怎么让系数等于零的),以及为什么L2正则化可以防止过拟合。
3.2.1 L1正则化和特征选择
稀疏模型与特征选择:
上面提到L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。为什么要生成一个稀疏矩阵?
稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,或者贡献微小(因为它们前面的系数是0或者是很小的值,即使去掉对模型也没有什么影响),此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。
假设有如下带L1正则化的损失函数:
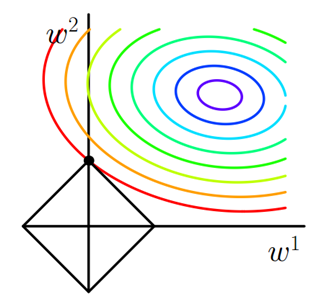
其中J0是原始的损失函数,加号后面的一项是L1正则化项,α是正则化系数。注意到L1正则化是权值的绝对值之和,J是带有绝对值符号的函数,因此J是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。当我们在原始损失函数J0后添加L1正则化项时,相当于对J0做了一个约束。令L=![]() ,则J=J0+LJ,此时我们的任务变成在L约束下求出J0取最小值的解。考虑二维的情况,即只有两个权值w1和w2,此时L=|w1|+|w2|对于梯度下降法,求解J0的过程可以画出等值线,同时L1正则化的函数L也可以在w1、w2的二维平面上画出来。如下图:
,则J=J0+LJ,此时我们的任务变成在L约束下求出J0取最小值的解。考虑二维的情况,即只有两个权值w1和w2,此时L=|w1|+|w2|对于梯度下降法,求解J0的过程可以画出等值线,同时L1正则化的函数L也可以在w1、w2的二维平面上画出来。如下图:
图1 L1正则化
图中等值线是J0的等值线,黑色方形是L函数的图形。在图中,当J0等值线与L图形首次相交的地方就是最优解。上图中0J与L在L的一个顶点处相交,这个顶点就是最优解。注意到这个顶点的值是(w1,w2)=(0,w)。可以直观想象,因为L函数有很多『突出的角』(二维情况下四个,多维情况下更多),J0与这些角接触的机率会远大于与L其它部位接触的机率,而在这些角上,会有很多权值等于0,这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
而正则化前面的系数α,可以控制L图形的大小。α越小,L的图形越大(上图中的黑色方框);α越大,L的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值(w1,w2)=(0,w)中的w可以取到很小的值。
3.2.2 L2正则化和过拟合
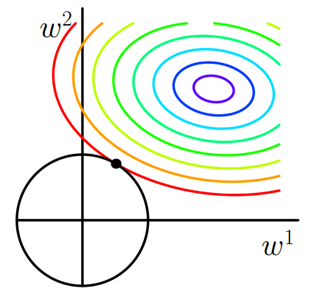
类似,假设有如下带L2正则化的损失函数:
同样可以画出他们在二维平面上的图形,如下:
图2 L2正则化
二维平面下L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此J0与L相交时使得w1或w2等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。
拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是『抗扰动能力强』。
那为什么L2正则化可以获得值很小的参数?
以线性回归中的梯度下降法为例。假设要求的参数为θ,hθ(x)是我们的假设函数,那么线性回归的代价函数如下:
那么在梯度下降法中,最终用于迭代计算参数θ的迭代式为:
其中α是learning rate. 上式是没有添加L2正则化项的迭代公式,如果在原始代价函数之后添加L2正则化,则迭代公式会变成下面的样子:
其中λ就是正则化参数。从上式可以看到,与未添加L2正则化的迭代公式相比,每一次迭代,θj都要先乘以一个小于1的因子,从而使得θj不断减小,因此总得来看,θ是不断减小的。
L2正则化参数:
从公式5可以看到,λ越大,θj衰减得越快。另一个理解可以参考图2, λ越大,L2圆的半径越小,最后求得代价函数最值时各参数也会变得很小。
4 如何用逻辑回归处理多标签问题
逻辑斯蒂回归本身只能用于二分类问题,如果实际情况是多分类的,那么就需要对模型进行一些改动,以下是三种比较常用的将逻辑斯蒂回归用于多分类的方法:
4.1 One vs One
OvO 的方法就是将多个类别中抽出来两个类别,然后将对应的样本输入到一个逻辑斯蒂回归的模型中,学到一个对这两个类别的分类器,然后重复以上的步骤,直到所有类别两两之间都存在一个分类器。
假设存在四个类别,那么分类器的数量为6个,表格如下:

分类器的数量直接使用 ![]() 就可以了,k 代表类别的数量。
就可以了,k 代表类别的数量。
在预测时,需要运行每一个模型,然后记录每个分类器的预测结果,也就是每个分类器都进行一次投票,取获得票数最多的那个类别就是最终的多分类的结果。
比如在以上的例子中,6个分类器有3个投票给了类别3,1个投票给了类别2,1个投票给类别1,最后一个投票给类别0,那么就取类别3为最终预测结果。
OvO 的方法中,当需要预测的类别变得很多的时候,那么我们需要进行训练的分类器也变得很多了,这一方面提高了训练开销,但在另一方面,每一个训练器中,因为只需要输入两个类别对应的训练样本即可,这样就又减少了开销。
从预测的角度考虑,这种方式需要运行的分类器非常多,而无法降低每个分类器的预测时间复杂度,因此预测的开销较大。
4.2 One vs All
针对问题:一个样本对应多个标签。
OvA 的方法就是从所有类别中依次选择一个类别作为1,其他所有类别作为0,来训练分类器,因此分类器的数量要比 OvO 的数量少得多。

通过以上例子可以看到,分类器的数量实际上就是类别的数量,也就是k。
虽然分类器的数量下降了,但是对于每一个分类器来说,训练时需要将所有的训练数据全部输入进去进行训练,因此每一个分类器的训练时间复杂度是高于 OvO 的。
从预测的方面来说,因为分类器的数量较少,而每个分类器的预测时间复杂度不变,因此总体的预测时间复杂度小于 OvA。
预测结果的确定,是根据每个分类器对其对应的类别1的概率进行排序,选择概率最高的那个类别作为最终的预测类别。
4.3 从sigmoid函数到softmax函数的推导
针对问题:一个样本对应一个标签。
第三种方式,我们可以直接从数学上使用 softmax 函数来得到最终的结果,而 softmax 函数与 sigmoid 函数有着密不可分的关系,它是 sigmoid 函数的更一般化的表示,而 sigmoid 函数是 softmax 函数的一个特殊情况。


分子代表的是一件事发生的概率,分母代表这件事以外的事发生的概率,两者的和为1。

当我们面对的情况是多个分类时,可以让 k-1 个类别分别对剩下的那个类别做回归,即得到 k-1 个 logit 公式:

然后对这些公式稍微变个型,可得:
![]()
由于我们知道所有类别的可能性相加为1,因此可以得到:

通过解上面的方程,可以得到关于某个样本被分类到类别 ![]() 的概率:
的概率:

这就是我们所了解的 softmax 函数了。
5 为什么逻辑斯蒂回归的输出值可以作为概率
指数分布族函数与广义线性模型(Generalized Linear Models,GLM)_意念回复的博客-CSDN博客_广义线性模型连接函数
面试题解答:为什么逻辑斯蒂回归的输出值可以作为概率 - 知乎
因为逻辑斯蒂回归(Logistic Regression)的 sigmoid 函数是符合广义线性模型(General Linear Model)的伯努利分布(Bernoulli Distribution)的规范联系函数(Canonical Link Function)的反函数,sigmoid 函数将线性函数映射到伯努利分布的期望。
在刚开始学习机器学习的时候,很多教材会告诉你,在逻辑斯蒂回归中,我们使用 sigmoid 函数将预测值从实数域转换为(0,1)区间内,而这可以代表该预测值为正类或为负类的概率。
这样的表达方式,让初学者很容易陷入一个误区,即当我们将其转换为(0,1)区间后,就可以代表概率了,这是不太恰当的。通过对广义线性模型的研究,发现是因为 sigmoid 函数将实数域转换为了概率,所以其值落在(0,1)区间之内。
下面将详细地说明,为什么中,使用 sigmoid 函数,就可以得到概率。
首先,给出一个问题推导和本文行文思路的图,看不懂的时候可以参考下图:

因为 sigmoid 函数是伯努利分布的联系函数的反函数,它将线性函数映射到了伯努利分布的期望上,而伯努利分布的期望本身就是概率,因此,我们最终从逻辑斯蒂回归得到的输出,可以代表概率,也正是因为它代表概率,才落在(0,1)之间。
6 逻辑斯蒂回归是否可以使用其他的函数替代 sigmoid 函数
sigmoid 函数的使用是一个自然而然的选择,但却并不是必须的选择,对 sigmoid 函数进行一个简单的变化,也可以得到不错的模型效果,比如,sigmoid 函数中以自然常数 e 作为底,我们可以将其换成其他的数值,比如2,或者10:

这些函数画出来如下图,可以看到它们都将实数域映射到了(0,1)之间,但除了以自然常数 e 为底的 sigmoid 函数外,其他函数都无法通过广义线性模型推导出来,因此它们不是伯努利分布的正则联系函数(Canonical Link Function)。

不使用 sigmoid 函数的形式,而采用其他的形式呢,比如 tanh 函数
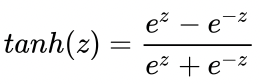

显然,如果使用 tanh 函数的话,将会把实数值域映射到(-1, 1)之间,因此我们将用0作为判断预测值为1或-1的阈值。
同时,我们将交叉熵损失函数换成均方误差:
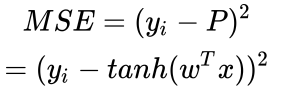
当然,这样做下来,所谓的逻辑斯蒂回归已经不存在了,而是一个由我们自己搭配映射函数和损失函数的分类模型。
那么我们看下以 tanh 为映射函数,以 MSE 为损失函数的情况下,如何对参数进行梯度下降,让我们对 MSE 求 w 的偏导:

这样我们就得到了参数的梯度,可以进行梯度下降法优化模型了。
其实我们在应用模型的时候,不应该一直照搬书中的公式,更不应该发现模型效果不好,就换一个模型,而是应该在学习模型的时候,去学习模型的思路,这样我们在遇到实际的工程问题时,才能明白到底哪里有问题,以及如何对模型进行修正,才不会成为调包侠。
如何优雅地将二项逻辑斯蒂回归模型推广为多项逻辑斯蒂回归模型? - 知乎
其他面试题解答:
面试题解答1:为什么线性回归要求假设因变量符合正态分布 - 知乎 (zhihu.com)
面试题解答2:各种回归模型与广义线性模型的关系 - 知乎 (zhihu.com)
面试题解答3:如何用方差膨胀因子判断多重共线性 - 知乎 (zhihu.com)
面试题解答4:逻辑斯蒂回归是否可以使用其他的函数替代 sigmoid 函数 - 知乎 (zhihu.com)
面试题解答5:特征存在多重共线性,有哪些解决方法? - 知乎 (zhihu.com)
面试题解答6:逻辑斯蒂回归为什么使用交叉熵而不是MSE - 知乎 (zhihu.com)
对于多元逻辑回归,可用如下公式似合分类,其中公式(4)的变换,将在逻辑回归模型参数估计时,化简公式带来很多益处,y={0,1}为分类结果。