逻辑回归模型详解(Logistic Regression)

广义线性模型

极大似然法

逻辑回归的假设函数

逻辑回归的损失函数

交叉熵损失函数

为什么LR模型损失函数使用交叉熵不用均方差

交叉熵损失函数的数学原理

交叉熵损失函数的直观理解

交叉熵简介

对数损失函数和交叉熵损失函数

逻辑回归优缺点

其他

逻辑回归与线性回归的区别与联系

LR一般需要连续特征离散化原因

广义线性模型

逻辑回归与线性回归都是一种广义线性模型（generalized linear model，GLM）。具体的说，都是从指数分布族导出的线性模型，线性回归假设Y|X服从高斯分布，逻辑回归假设Y|X服从伯努利分布。

伯努利分布：伯努利分布又名0-1分布或者两点分布，是一个离散型概率分布。随机变量X只取0和1两个值，比如正面或反面，成功或失败，有缺陷或没有缺陷，病人康复或未康复。为方便起见，记这两个可能的结果为0和1，成功概率为p(0<=p<=1)，失败概率为q=1-p。

高斯分布：高斯分布一般指正态分布。

因此逻辑回归与线性回归有很多相同之处，去除Sigmoid映射函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

这两种分布都是属于指数分布族，我们可以通过指数分布族求解广义线性模型（GLM）的一般形式，导出这两种模型，具体的演变过程如下：

（此部分参考：https://zhuanlan.zhihu.com/p/81723099）

极大似然法

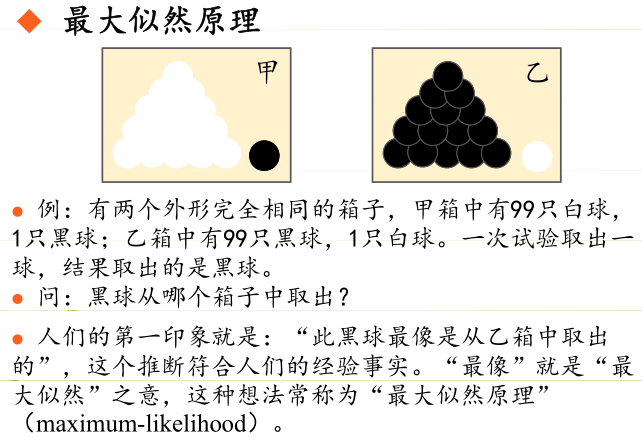
极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值。

极大似然估计的原理，用一张图片来说明，如下图所示：

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。

极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

逻辑回归的假设函数

首先我们要先介绍一下Sigmoid函数，也称为逻辑函数（Logistic function）：

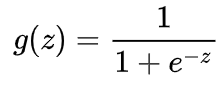
其函数曲线如下：

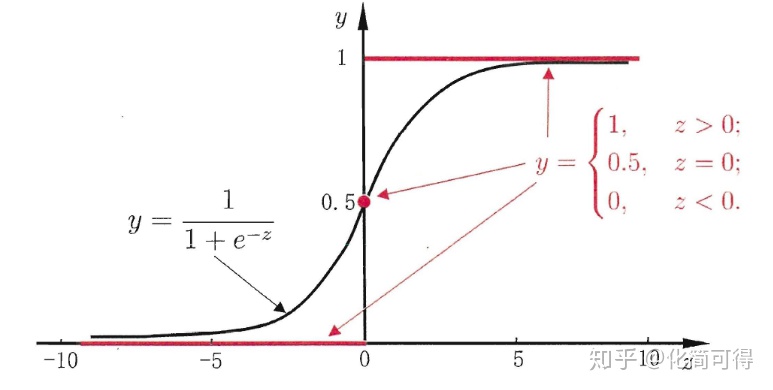
从上图可以看到sigmoid函数是一个s形的曲线，它的取值在[0, 1]之间，在远离0的地方函数的值会很快接近0或者1，它的这个特性对于解决二分类问题十分重要。

逻辑回归的假设函数形式如下：

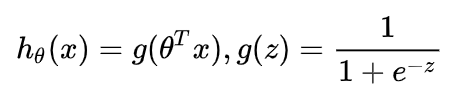
所以：

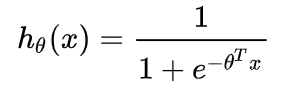
其中 x 是我们的输入，θ 为我们要求取的参数。

一个机器学习的模型，实际上是把决策函数限定在某一组条件下，这组限定条件就决定了模型的假设空间。当然，我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是：

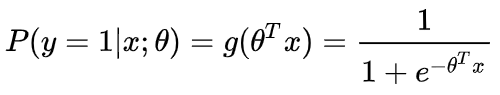
这个函数的意思就是在给定 x 和 θ 的条件下，y = 1的概率。

逻辑回归的损失函数

通常提到损失函数，我们不得不提到代价函数（Cost Function）及目标函数（Object Function）。

损失函数（Loss Function) 直接作用于单个样本，用来表达样本的误差

代价函数（Cost Function）是整个样本集的平均误差，对所有损失函数值的平均

目标函数（Object Function）是我们最终要优化的函数，也就是代价函数+正则化函数（经验风险+结构风险）

概况来讲，任何能够衡量模型预测出来的值 h(θ) 与真实值 y 之间的差异的函数都可以叫做代价函数 C(θ) 如果有多个样本，则可以将所有代价函数的取值求均值，记做 J(θ) 。因此很容易就可以得出以下关于代价函数的性质：

选择代价函数时，最好挑选对参数 θ 可微的函数（全微分存在，偏导数一定存在）
对于每种算法来说，代价函数不是唯一的；
代价函数是参数 θ 的函数；
总的代价函数 J(θ) 可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本（x,y）；
J(θ) 是一个标量；

经过上面的描述，一个好的代价函数需要满足两个最基本的要求：能够评价模型的准确性，对参数 θ 可微。

在线性回归中，最常用的是均方误差(Mean squared error)，即

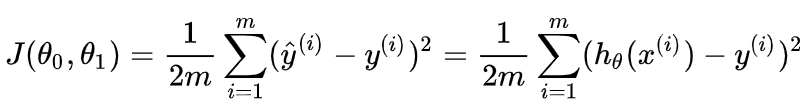
在逻辑回归中，最常用的是代价函数是交叉熵(Cross Entropy)，交叉熵是一个常见的代价函数

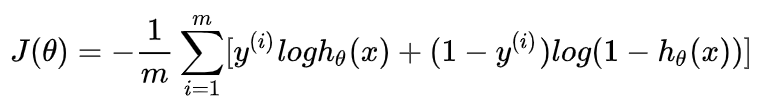
通过梯度下降法求参数的更新式

我们下图为推倒式，这样可以使推导式更简洁。

求梯度：

学习率

LR在确定了模型的形式后，通过最大似然估计法来实现最小散度从而求出模型参数。

交叉熵损失函数

说起交叉熵损失函数「Cross Entropy Loss」，脑海中立马浮现出它的公式：

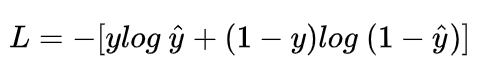
为什么LR模型损失函数使用交叉熵不用均方差

交叉熵损失函数的数学原理

我们知道，在二分类问题模型：例如逻辑回归「Logistic Regression」、神经网络「Neural Network」等，真实样本的标签为 [0，1]，分别表示负类和正类。模型的最后通常会经过一个 Sigmoid 函数，输出一个概率值，这个概率值反映了预测为正类的可能性：概率越大，可能性越大。

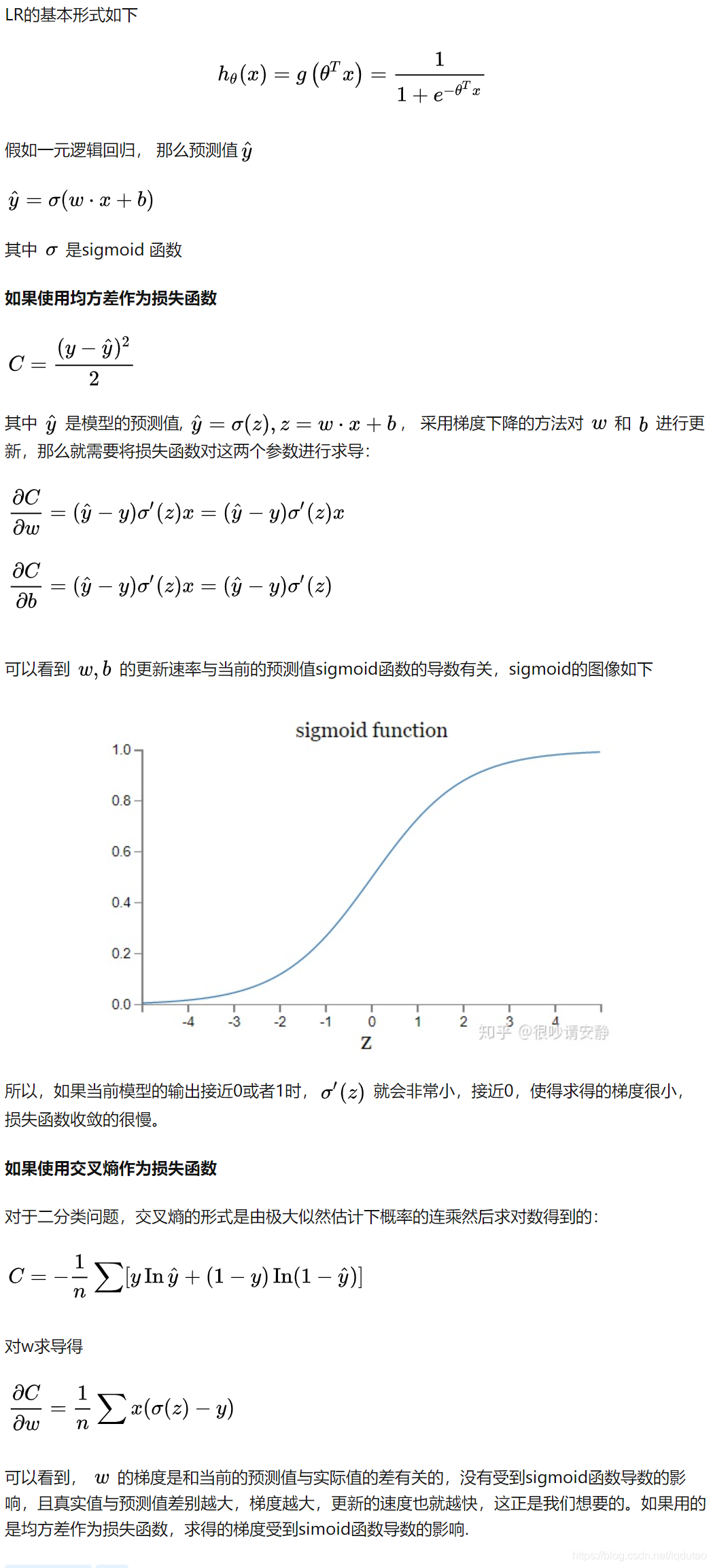
Sigmoid 函数的表达式和图形如下所示：

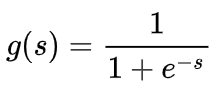
其中 s 是模型上一层的输出，Sigmoid 函数有这样的特点：s = 0 时，g(s) = 0.5；s >> 0 时， g ≈ 1，s << 0 时，g ≈ 0。显然，g(s) 将前一级的线性输出映射到 [0，1] 之间的数值概率上。这里的 g(s) 就是交叉熵公式中的模型预测输出。

我们说了，预测输出即 Sigmoid 函数的输出表征了当前样本标签为 1 的概率：

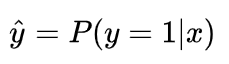
很明显，当前样本标签为 0 的概率就可以表达成：

重点来了，如果我们从极大似然性的角度出发，把上面两种情况整合到一起：

不懂极大似然估计也没关系。我们可以这么来看：

当真实样本标签 y = 0 时，上面式子第一项就为 1，概率等式转化为：

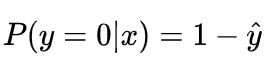
当真实样本标签 y = 1 时，上面式子第二项就为 1，概率等式转化为：

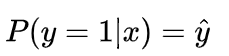
两种情况下概率表达式跟之前的完全一致，只不过我们把两种情况整合在一起了。

重点看一下整合之后的概率表达式，我们希望的是概率 P(y|x) 越大越好。首先，我们对 P(y|x) 引入 log 函数，因为 log 运算并不会影响函数本身的单调性。则有：

我们希望 log P(y|x) 越大越好，反过来，只要 log P(y|x) 的负值 -log P(y|x) 越小就行了。那我们就可以引入损失函数，且令 Loss = -log P(y|x)即可。则得到损失函数为：

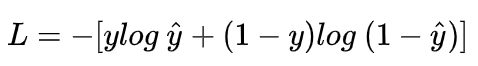
非常简单，我们已经推导出了单个样本的损失函数，是如果是计算 N 个样本的总的损失函数，只要将 N 个 Loss 叠加起来就可以了：

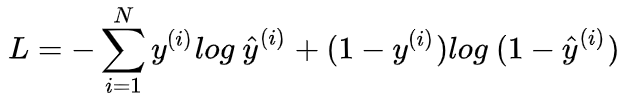
这样，我们已经完整地实现了交叉熵损失函数的推导过程。

交叉熵损失函数的直观理解

从图形的角度，分析交叉熵函数，加深大家的理解。首先，还是写出单个样本的交叉熵损失函数：

我们知道，当 y = 1 时：

这时候，L 与预测输出的关系如下图所示：

看了 L 的图形，简单明了！横坐标是预测输出，纵坐标是交叉熵损失函数 L。显然，预测输出越接近真实样本标签 1，损失函数 L 越小；预测输出越接近 0，L 越大。因此，函数的变化趋势完全符合实际需要的情况。

当 y = 0 时：

这时候，L 与预测输出的关系如下图所示：

同样，预测输出越接近真实样本标签 0，损失函数 L 越小；预测函数越接近 1，L 越大。函数的变化趋势也完全符合实际需要的情况。

从上面两种图，可以帮助我们对交叉熵损失函数有更直观的理解。无论真实样本标签 y 是 0 还是 1，L 都表征了预测输出与 y 的差距。

另外，重点提一点的是，从图形中我们可以发现：预测输出与 y 差得越多，L 的值越大，也就是说对当前模型的 “ 惩罚 ” 越大，而且是非线性增大，是一种类似指数增长的级别。这是由 log 函数本身的特性所决定的。这样的好处是模型会倾向于让预测输出更接近真实样本标签 y。

交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小，模型预测效果就越好。
交叉熵在分类问题中常常与softmax是标配，softmax将输出的结果进行处理，使其多个分类的预测值和为1，再通过交叉熵来计算损失。

交叉熵可在神经网络(机器学习)中作为损失函数，p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。

交叉熵简介

交叉熵是信息论中的一个重要概念，主要用于度量两个概率分布间的差异性，要理解交叉熵，需要先了解下面几个概念。

信息量

信息奠基人香农（Shannon）认为“信息是用来消除随机不确定性的东西”，也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。

“太阳从东边升起”，这条信息并没有减少不确定性，因为太阳肯定是从东边升起的，这是一句废话，信息量为0。

”2018年中国队成功进入世界杯“，从直觉上来看，这句话具有很大的信息量。因为中国队进入世界杯的不确定性因素很大，而这句话消除了进入世界杯的不确定性，所以按照定义，这句话的信息量很大。

根据上述可总结如下：信息量的大小与信息发生的概率成反比。概率越大，信息量越小。概率越小，信息量越大。

设某一事件发生的概率为P(x)，其信息量表示为：

其中 I ( x ) 表示信息量，这里 log 表示以e为底的自然对数。

信息熵

信息熵也被称为熵，用来表示所有信息量的期望。

期望是试验中每次可能结果的概率乘以其结果的总和。

所以信息量的熵可表示为：（这里的X XX是一个离散型随机变量）

使用明天的天气概率来计算其信息熵：

对于0-1分布的问题，由于其结果只用两种情况，是或不是，设某一件事情发生的概率为P ( x ) ，则另一件事情发生的概率为1 − P ( x ) ，所以对于0-1分布的问题，计算熵的公式可以简化如下：

相对熵（KL散度）

如果对于同一个随机变量X XX有两个单独的概率分布 P(x) 和 Q(x)，则我们可以使用KL散度来衡量这两个概率分布之间的差异。

下面直接列出公式，再举例子加以说明。

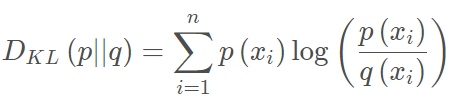
在机器学习中，常常使用 P(x) 来表示样本的真实分布，Q(x) 来表示模型所预测的分布，比如在一个三分类任务中（例如，猫狗马分类器）， x1,x2,x3 分别代表猫，狗，马，例如一张猫的图片真实分布 P(X)=[1,0,0] ，预测分布 Q(X)=[0.7,0.2,0.1] ，计算KL散度：

KL散度越小，表示 P(x) 与 Q(x) 的分布更加接近，可以通过反复训练 Q(x) 来使 Q(x) 的分布逼近 P(x)。

交叉熵

首先将KL散度公式拆开：

前者 H(p(x)) 表示信息熵，后者即为交叉熵，KL散度 = 交叉熵 - 信息熵

交叉熵公式表示为：

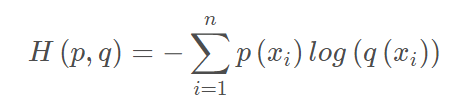
在机器学习训练网络时，输入数据与标签常常已经确定，那么真实概率分布 P(x) 也就确定下来了，所以信息熵在这里就是一个常量。由于KL散度的值表示真实概率分布 P(x) 与预测概率分布 Q(x) 之间的差异，值越小表示预测的结果越好，所以需要最小化KL散度，而交叉熵等于KL散度加上一个常量（信息熵），且公式相比KL散度更加容易计算，所以在机器学习中常常使用交叉熵损失函数来计算loss就行了。

对数损失函数和交叉熵损失函数

逻辑回归优缺点

LR优点：

直接对分类的可能性建模，无需事先假设数据分布，避免了假设分布不准确带来的问题
不仅预测出类别，还可得到近似概率预测
对率函数是任意阶可导凸函数，有很好得数学性质，很多数值优化算法可直接用于求取最优解
容易使用和解释，计算代价低
LR对时间和内存需求上相当高效
可应用于分布式数据，并且还有在线算法实现，用较小资源处理较大数据
对数据中小噪声鲁棒性很好，并且不会受到轻微多重共线性影响
因为结果是概率，可用作排序模型

LR缺点：

容易欠拟合，分类精度不高
数据特征有缺失或特征空间很大时效果不好

其他

逻辑回归与线性回归的区别与联系

区别

线性回归假设响应变量服从正态分布，逻辑回归假设响应变量服从伯努利分布
线性回归优化的目标函数是均方差（最小二乘），而逻辑回归优化的是似然函数（交叉熵）
线性归回要求自变量与因变量呈线性关系，而逻辑回归没有要求
线性回归分析的是因变量自身与自变量的关系，而逻辑回归研究的是因变量取值的概率与自变量的概率
逻辑回归处理的是分类问题，线性回归处理的是回归问题，这也导致了两个模型的取值范围不同：0-1和实数域
参数估计上，都是用极大似然估计的方法估计参数（高斯分布导致了线性模型损失函数为均方差，伯努利分布导致逻辑回归损失函数为交叉熵）

联系

两个都是线性模型，线性回归是普通线性模型，逻辑回归是广义线性模型
表达形式上，逻辑回归是线性回归套上了一个Sigmoid函数

LR一般需要连续特征离散化原因

离散特征的增加和减少都很容易，易于模型快速迭代
稀疏向量内积乘法速度快，计算结果方便存储，容易扩展
离散化的特征对异常数据有很强的鲁棒性(比如年龄为300异常值可归为年龄>30这一段)
逻辑回归属于广义线性模型，表达能力受限。单变量离散化为N个后，每个变量有单独的权重，相当于对模型引入了非线性，能够提升模型表达能力，加大拟合
离散化进行特征交叉，由 m+n 个变量为 m*n 个变量(将单个特征分成 m 个取值)，进一步引入非线性，提升表达能力
特征离散化后，模型会更稳定(比如对用户年龄离散化，20-30作为一个区间，不会因为用户年龄，增加一岁变成完全不同的人，但区间相邻处样本会相反，所以怎样划分区间很重要)
特征离散化后，简化了LR模型作用，降低模型过拟合风险

参考链接：https://blog.csdn.net/zengxiantao1994/article/details/72787849

交叉熵损失函数：https://zhuanlan.zhihu.com/p/35709485

参考链接：https://zhuanlan.zhihu.com/p/38241764